פורטל:מתמטיקה/תמונה נבחרת/גלריה

עריכהתמונה נבחרת

1

טבעת מביוס, צורה מרחבית (ליתר דיוק יריעה), המורכבת מסרט בעל צד אחד בלבד. טבעת מביוס היא הדוגמה הבסיסית ליריעה לא־אוריינטבילית. זאת אחת הסיבות לכך שטבעת מביוס משמשת כקוריוז מתמטי עבור חובבים.

2

אנך למשטח יוצר עמו זווית ישרה בנקודה ממנה הוא יוצא. באיור מיוצגים האנכים של מישור מסוים כשדה וקטורי. לאנכים מסוג זה שימוש רב באנליזה וקטורית.

3

הטסרקט, שהוא גוף ארבע ממדי המהווה הכללה של הקובייה, כפי שהוא נראה לאחר הטלה סטריאוגרפית מן ה-3-ספירה אל המרחב האוקלידי התלת ממדי, בעיניה של ג'ני.

4

קשת השער בסנט לואיס שבמיזורי היא מבנה מרשים הבנוי בצורת קוסינוס היפרבולי, הקרויה קו השרשרת. הקשת מסמלת את "שער הכניסה" למערב ארצות הברית ומוקדשת למתיישבים שפרצו את הדרך מערבה במאה ה-19.

5

האם אפשר לצבוע כל מפה מדינית, כך שכל שתי מדינות בעלות קו גבול משותף נצבעות בצבע שונה, תוך שימוש בארבעה צבעים בלבד?
משפט ארבעת הצבעים מבטיח כי הדבר אפשרי. משפט זה הוא תוצאה בולטת בהיסטוריה של הטופולוגיה הקומבינטורית ושל תורת הגרפים.

6

ברוקולי בצורת פרקטל, צורה החוזרת על עצמה מספר רב של פעמים כך שככל שנעמיק בה תתגלה אותה התבנית שוב ושוב.

7

מעגל היחידה הטריגונומטרי הוא כלי הנותן צורה נוחה לתיאורן של הפונקציות הטריגונומטריות ומאפשר את הרחבתן אל מעבר למחזור אחד. בתמונה משורטטות על המעגל הפונקציות הטריגנומטריות המרכזיות, כמו גם מספר פונקציות אשר אינן נמצאות יותר בשימוש, כדוגמת הפונקציה ${\text{exsec}}(\theta )$ .

8

חשבונייה סינית. עקב סיבות גיאופוליטיות, במשך שנים רבות התפתחה התרבות של סין העתיקה עם זיקה מעטה מאד לתרבויות אחרות. המתמטיקה הסינית, בשונה מהמתמטיקה היוונית, הייתה מתמטיקה תכליתית.
ראו גם: היסטוריה של האריתמטיקה.

9

בקבוק קליין, מוטבע במרחב התלת־ממדי. בקבוק קליין הוא משטח קומפקטי לא־אוריינטבילי, זאת אומרת שיש לו צד אחד בלבד. למרות שהמשטח הוא דו־ממדי, ודומה למישור בסביבה הקרובה של כל נקודה, הוא אינו ניתן לשיכון במרחב האוקלידי התלת־ממדי, אלא רק במרחב בעל ארבעה ממדים או יותר.

10

התחריט מלנכוליה, 1514. בשל החידתיות הרבה של יצירה זו, ריבוי האלמנטים הסימבוליים ועושר האלמנטים המתמטיים-גאומטריים שבה, היא אחת היצירות שזכו למספר רב של ניתוחים, דיונים ופרשנויות, במגוון נקודות מבט, שנייה אולי רק למונה ליזה של לאונרדו דה וינצ'י. מלנכוליה היא תחריט נחושת, ומוצגת במוזיאון לאמנות יפה שבבוסטון. היצירה כוללת, בין היתר, ריבוע קסם מסדר רביעי ופאון אשר מהווים חלק נכבד מהעברת הרעיון שביצירה.

11

סרטון של זום לתוך קבוצת מנדלברוט

סרטון של זום לתוך קבוצת מנדלברוט, קבוצה של מספרים מרוכבים אשר הגבול של ייצוגן הגאומטרי מהווה את אחת הדוגמאות המוכרות ביותר של פרקטלים במתמטיקה.

12

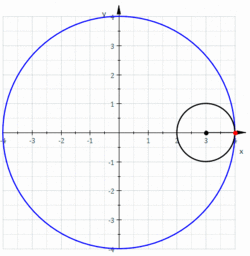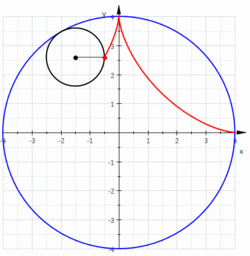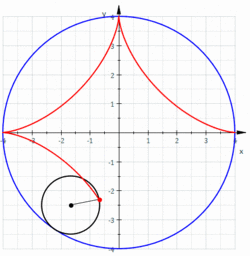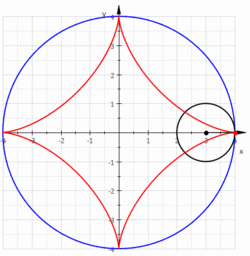
מסלולה של נקודה על שפתו של מעגל המתגלגל על שפתו מעגל אחר בעל רדיוס גדול פי ארבעה נקראת "אסטרואידה". משוואתה של אסטרואידה היא $x^{\frac {2}{3}}+y^{\frac {2}{3}}=1$ .

13

הקורטה הוא מחשבון מכני קטן שהושק לראשונה ב-1948. בתמונה: מחשבון קורטה מכני בתצוגה במוזיאון להיסטוריה של המחשב במאונטן ויו שבקליפורניה.

14

ישרים חשובים במשולש: ישר אוילר באדום, אנכים אמצעיים בצהוב, תיכונים בכחול וגבהים בירוק.

15

פאון בן 1860 קודקודים ו- 5340 צלעות.

16

ציור של לוקה פאצ'ולי מלמד, מיוחס ליאקופו דה ברברי מ-1495. השולחן מלא בכלים גאומטריים: לוח צפחה, גיר, מחוגה, הספר שכתב ודגם של דודקהדרון. רומביקובוקטהדרון שחציו מלא במים תלוי מהתיקרה. פאצ'ולי מדגים משפט מתמטי של אוקלידס.

17

יחס הזהב הוא קבוע מתמטי המעסיק את המדע והאמנות כבר מאות בשנים. יחס הזהב, שערכו כ- 1.618, מסומן באות היוונית פי ($\varphi$). זהו יחס המייצג מידות וגדלים רבים בטבע והחל מתקופת יוון הקלאסית הוא גם משמש באמנות ובאדריכלות. בתמונה, מוצגת כיכר בכפר ההולנדי ברוסלה, שתוכננה על פי יחס הזהב.

18

כוכב פנרוז. בעזרת אריחי פנרוז ניתן לרצף את המישור.

19

פרקטל היא צורה החוזרת על עצמה פעמים רבות ברמות התבוננות שונות. לפרקטלים תכונות מתמטיות מעניינות רבות. כך, למשל, לעתים ממדיהם אינם שלמים או שהיקפם הנו אינסופי בעוד ששטחם סופי. כיום, עם תפוצת המחשבים והנגישות לתוכנה חופשית, יכול כל אחד ליצור פרקטלים מרהיבים בקלות יחסית, כמו זה אשר בתמונה.

20

משולש, כפי שהוא נראה במערכות גאומטריות שונות. המשולש התחתון הנו משולש המתקיים בגאומטריה האוקלידית. המשלוש האמצעי מתקיים בגאומטריה היפרבולית והעליון בגאומטריה ספירית.

21

אנימציה תלת-ממדית המציגה את היטליו של טסרקט, גוף ארבע ממדי המהווה הכללה של הקובייה התלת ממדית.

22

"קשר טורוס" הוא קשר המלופף על פניו של טורוס. קשר זה מקובל לאפיין על ידי שני מספרים זרים, q ו-p, כאשר q הוא מספר הליפופים על הטורוס ו- p הוא מספר הפעמים בו הוא עובר דרך ה"חור" שבמרכז הטורוס.

23

קונכיית נאוטילוס, בצורת ספירלה לוגריתמית.

24

הספרות הבבליות הכתובות בבסיס סקסגסימלי (כלומר, בסיס 60). ניתן להבחין בנקל בשיטת הקיבוץ המשנית בה השתמשו הבבלים.
ראו גם: היסטוריה של האריתמטיקה.

25

איור הממחיש את מושג האינטגרל הקווי.

26

ציקלואידה
עקומה המתארת את מסלולה של נקודה קבועה על גבי מעגל המתגלגל ללא החלקה על גבי קו ישר. זה המסלול הפותר את בעיית הברכיסטוכרון, בעיית "הזמן הקצר ביותר".

27

ייצוג תלת ממדי של טנזור לוי-צ'יוויטה, אשר איבריו מוגדרים על ידי סימן לוי-צ'יוויטה. באמצעות סימון זה, מתאפשר במקרים מסוימים לקצר את רישומן של פעולות על וקטורים ועל טנזורים.

28

גרדיאנט הינו אופרטור וקטורי המופעל על שדה סקלרי. הגרדיאנט של שדה סקלרי הוא שדה וקטורי המשייך לכל נקודה במרחב וקטור המצביע אל הכיוון בו השינוי בשדה הסקלרי מקסימלי (חיובי), ואשר גודלו כשיעור השינוי המקסימלי.
באיורים האלה, השדה הסקלרי מתואר באמצעות שינוי הצבע, כאשר אזורים כהים יותר הם ערכים גדולים יותר של הפונקציה. החצים הכחולים מתארים את הגרדיאנט הנגזר מהשדה הסקלרי. החצים פונים אל עבר האזורים הגבוהים יותר.

29

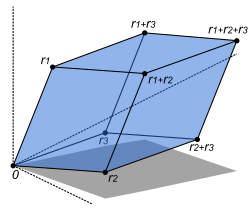
דטרמיננטה של מטריצה ריבועית היא סקלר התלוי ברכיבי המטריצה, ושווה לאפס בדיוק כאשר המטריצה אינה הפיכה. אם למטריצה ריבועית ישנם מקדמים ממשיים, אזי הדטרמיננטה שלה שווה לנפחו של המקבילון (במרחב האוקלידי ה- $n$-ממדי), שקודקודיו הם עמודות המטריצה.

30

"החילזון של מביוס" הנוצר על ידי קיפול השפה של רצועת מביוס מעל שדה המספרים המרוכבים וביצוע הטלה סטריאוגרפית שלה על המספרים הממשיים.
לחצו על התמונה להגדלה.

31

המחשת מושג האינטגרל של רימן, שהוא חישוב השטח מתחת לגרף של פונקציה על ידי חלוקתו למלבנים קטנים יותר ויותר וסכימת שטחיהם. ככל שנסכמים מלבנים רבים יותר, כך הקירוב משתפר. כך, כאשר כמות המלבנים הנסכמים מתקרבת לאינסוף, השטח המתקבל מתקרב לשטח המקורי.

32

עצם אישנגו. רבים טוענים שהיא ראיה להבנתו של האדם את האריתמטיקה הפשוטה עוד בשנים 20,000-18,000 לפני הספירה.
ראו גם: היסטוריה של האריתמטיקה.

33

זווית בגודל של רדיאן אחד נוצרת על ידי קשת שהיקפה שווה לאורך של רדיוס המעגל.

34

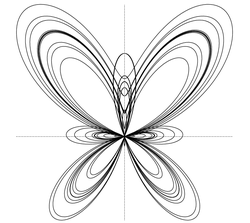
"עקומת פרפר טרנסצנדנטלית" היא עקום המתואר על ידי הפרמטריזציה
$x=\sin(t)\left(e^{\cos(t)}-2\cos(4t)-\sin ^{5}\left({t \over 12}\right)\right)$
$y=\cos(t)\left(e^{\cos(t)}-2\cos(4t)-\sin ^{5}\left({t \over 12}\right)\right)$
או על ידי המשוואה הקוטבית $r=e^{\sin \theta }-2\cos(4\theta )+\sin ^{5}\left({\frac {2\theta -\pi }{24}}\right)$.

35

בדידים. השימוש בבדידים ככלי הוראה מרכזי בהקניית מושגים אריתמטיים בסיסיים נמצא במחלוקת חריפה הן בישראל והן מחוצה לה.
ראו גם: הוראת המתמטיקה בישראל.

36

מה הדרך הקצרה ביותר, מבין 43,589,145,600 דרכים אפשריות, לעבור ב-15 ערים מרכזיות בגרמניה?

זוהי דוגמה לבעיית הסוכן הנוסע, בעיה ידועה בתורת הגרפים ובתורת הסיבוכיות.

37

שעון בינארי. בשעון זה מיוצגות הספרות בבסיס בינארי, בסיס אשר פותח על ידי גוטפריד וילהלם לייבניץ במאה ה-17.

38

קובץ:Brazil.Brasilia.01.jpg

קתדרלת ברזיליה הבנויה בצורת היפרבולואיד, צורה אשר נועדה לייצג זוג ידיים הנישאות לשמיים.

משוואתו של היפרבולואיד מצורה זו הנה :${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1$.

39

מכפלה מעורבת של וקטורים נותנת את הנפח אשר כולא המקבילון שהם פורשים. זהו נפח מכוון אשר סימנו תלוי בסדר ביצוע הכפילה, דבר הבא לידי ביטוי בהוספת הסימן $\wedge$ המורה על סדר הכפילה.

40

אנימציה המדגימה את הרעיון העומד מאחורי משולש פסקל המאפשר חישוב של המקדמים הבינומיים.

41

איקוסהדרון הוא פאון משוכלל בעל עשרים פאות, אשר כל אחת מהן היא משולש משוכלל, כלומר משולש שכל צלעותיו וכל זוויותיו זהות. האיקוסהדרון הוא אחד מחמשת הגופים האפלטוניים. פאון זה ידוע גם כקוביית ק20 במשחקי תפקידים כגון מבוכים ודרקונים.

42

טורוס הנו גוף סיבוב הנוצר מסיבובו של מעגל סביב לציר הציב לו אך לא חותך אותו. בתמונה מופיע טורוס עם חור ההולך וגדל עד שהטורוס "בולע" את עצמו.

43

דיסק עזר למציאת ערכי פונקציות טריגונומטריות המתוארך לתקופת המאה ה-16.

44

ריצוף של המרחב ההיפרבולי התלת-ממדי בקוביות.

45

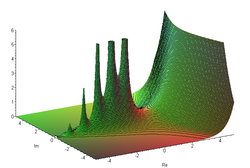
גרף של הערך המוחלט של פונקציית גמא במישור המרוכב.

46

כיצד ניתן לחתוך צלב יווני למספר קטן ככל האפשר של חלקים שמהם ניתן להרכיב ריבוע? את הפתרון הנראה בציור מצא הרי לינדגרן, אותו גילה בעזרת שיטה המבוססת על ריצופים, הנראית גם היא באיור.

47

ספירלת תאודורוס. זוהי הוכחה אינדוקטיבית שלכל מספר טבעי n, ניתן לבנות בעזרת סרגל ומחוגה קטע באורך ${\sqrt {n}}$. לאחר בנית קטע באורך ${\sqrt {n-1}}$, בונים משולש ישר-זווית שאורכי ניצביו הם ${\sqrt {n-1}}$ ו-$1\,$. ממשפט פיתגורס אנו יודעים כי אורך היתר הוא ${\sqrt {n}}$.

48

תמונה של רקמה מהוואי המבוססת על ריצוף של המישור, ומקיימת את חבורת הסימטריה pmg - הריצוף סימטרי תחת סיבוב ב-180 בשני צירים שונים, סימטרי תחת שיקוף בציר אחד, ותחת שיקוף מוזז בציר אחד, נוסף על סימטריות להזזה בשני כיוונים שונים.

49

קירוב של הפונקציה $e^{x}\,$ לפולינום מדרגה n באמצעות פיתוח לטור מקלורן.

50

משפט פיתגורס, הוא אחד מהמשפטים הגאומטריים הנודעים ביותר. הוא קובע שסכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר. באנימציה רואים את אחת מההוכחות הרבות למשפט. בעזרת חיתוך ל-4 משולשים ישרי זווית וסידור החלקים מחדש מתקבלת הוכחה של המשפט.

51

מנסרה היא צורה מרחבית אשר לה שני בסיסים חופפים ומקבילים. אם הבסיס הוא עיגול, מתקבל גליל. מגדלי עזריאלי בתל אביב הם (מימין לשמאל) בדמות מנסרה ריבועית, גליל ומנסרה משולשת.

52

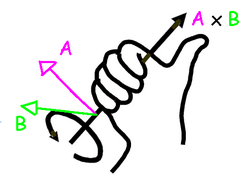
מכפלה וקטורית היא פעולה בינארית על שני וקטורים במרחב תלת ממדי, שמחזירה וקטור. בתמונה מופיע כלל עזר למציאת כיוונה המוכר בשם "כלל יד ימין": אם האצבעות מתוות את הקשת הקצרה מהווקטור הראשון לווקטור השני, האגודל מצביע בכיוון תוצאת המכפלה.

53

שימוש בשיטת המיצוי לחישוב ערכו של הקבוע פאי. שיטה זו מתבססת על כך שהיקף המעגל קטן מהיקפו של מצולע החוסם את המעגל וגדול מהיקפו של מצולע החסום במעגל. באמצעות חישוב ההיקף של מצולע חוסם ומצולע חסום בעלי מספר הולך וגדל של צלעות מושג דיוק גדל והולך של היקף המעגל, ובהתאם לכך דיוק גדל והולך של פאי. שיטה זו מיוחסת לארכימדס.

54

תמונה הממחישה את הגדרת הקואורדינטות הכדוריות. במערכת קואורדינטות זו, מיוצגת כל נקודה במרחב התלת ממדי על ידי מרחקה מראשית הצירים, הזווית שנוצרת בין קו המחבר אותה לראשית לבין ציר ה-z והזווית הנפרשת בין היטל קו זה על מישור xy לבין ציר ה- x.

55

תיאור גרפי של השדה הווקטורי $\ (-y,x)$.

56

פונקציית ויירשטראס היא הדוגמה הראשונה שפורסמה לפונקציה רציפה בכל נקודה על הישר הממשי אך לא גזירה באף נקודה.

57

מציאת כל המספרים הראשוניים בין 2 ל-120 באמצעות הנפה של ארטוסתנס.

58

הטרנספורמציה $(x,y)\mapsto (x,{\sqrt {|x|}}-y)$ מעבירה מעגל לצורת לב. צורה שקולה להצגת אותו הלב היא על ידי הפרמטריזציה $(r\cos(t),{\sqrt {|r\cos(t)|}}-r\sin(t));t\in [0,2\pi ]$, כאשר הפרמטר $\ r$ הוא מספר כלשהו.

59

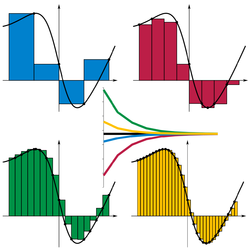
טור פורייה הוא כלי מתמטי המאפשר פירוק של פונקציות לרכיבים מחזוריים על ידי שימוש בפונקציות טריגונומטריות. בתמונה מופיע פירוק של גל מלבני בעל משרעת 4 וזמן מחזור של 1 לפונקציות סינוס על ידי הנוסחה $f(t)=2-{\frac {4}{\pi }}\sum _{n=1}^{k}{{\frac {(-1)^{n}-1}{n}}\sin(2\pi nt)}$.

הקו האדום מראה את הפונקציה המקורית, הירוק מראה את הפונקציה המתקבלת לאחר סכימת חמישה איברים והכחול לאחר סכימת חמישה עשר איברים. ככל שמסכמים איברים רבים יותר, כך מתקבלת פונקציה שערכיה קרובים יותר אל הפונקציה המקורית.

הטור מתכנס נקודתית בכל נקודות הרציפות של הגל. בנקודות האי-רציפות הוא מתכנס לממוצע בין הגבול מימין ומשמאל (בדוגמה זו ל-2). אולם הטור לא מתכנס במידה שווה. ניתן לראות כי כאשר מתקרבים לנקודת האי רציפות, יש פיק להפרש בין הסכומים החלקיים לבין הגבול. פיק זה הופך צר יתר אך גובהו חסום מלרע. תופעה זאת נקרת תופעת גיבס. לטור פורייה חשיבות רבה במתמטיקה תאורטית אבל גם שימוש נרחב בפיזיקה וישום מעשי כמו עיבוד אותות, תמונה וקול במדעי המחשב ושטחי הנדסה אחרים.

ניתן ללחוץ על התמונה על מנת לצפות בה מוגדלת.

60

זוויות אוילר הן שלוש זוויות במרחב האוקלידי המשמשות לתאר סיבוב בשלושה ממדים. כיוון שכל סיבוב כללי במרחב תלת-ממדי ניתן לייצוג על ידי הרכבה של שלושה סיבובים, ניתן לתאר כל סיבוב נתון על ידי שלוש זוויות אלו. לזוויות אוילר שימושים בפיזיקה ובפרט בתחום המכניקה של גוף קשיח.

61

בנייה של פתית השלג של קוך, פרקטל שתואר לראשונה על ידי הלגה פון קוך.

62

בתורת הקשרים המתמטית, טבעות בורומאיות הן שזר המורכב משלושה מעגלים טופולוגיים הכרוכים זה בזה באופן שהוצאת כל אחת מהטבעות משחררת את הקשר בין שתי האחרות. הטבעות קרויות על-שם חלק משלט האצולה של בית בורומאו ממילאנו של המאה ה-15.

63

עץ פיתגורס הוא פרקטל במישור שנתגלה על ידי אלברט בוסמן, המתקבל מבנייה בת אינסוף שלבים. הוא קרוי על שם המתמטיקאי היווני בן העת העתיקה פיתגורס, בשל העובדה שכל שלושה ריבועים סמוכים בפרקטל יוצרים משולש ישר-זווית, ולכן מקיימים את משפט פיתגורס. עץ הפיתגורס שבתמונה צבוע כך ששלבים תחילתיים בבנייתו צבועים בצהוב ושלבים מתקדמים בירוק.

64

כיסוי האוריינטציות של טבעת מביוס.

כיסוי האוריינטציות הוא כלי לחקר יריעות לא אוריינטביליות. עבור משטח במרחב, ניתן לתאר את כיסוי האוריינטציות באופן הבא: נדמיין שהמשטח עשוי מנייר דו-שכבתי. נפריד את השכבות. היריעה שתתקבל תהיה מרחב הכיסוי של כיסוי האוריינטציות. העתקת הכיסוי תהיה ההדבקה של שתי השכבות בחזרה.

במקרה של טבעת מביוס (זאת אומרת טבעת עם חצי פיתול) היריעה המתקבלת לאחר הפרדת השכבות היא טבעת עם פיתול שלם. יריעה זאת דיפאומורפית לטבעת רגילה, ובפרט אוריינטבילית.

65

תצוגה גרפית של כל הסודרים מ-0 עד $\omega ^{\omega }$

קבוצת סודרים זו מהווה סודר בפני עצמה. הוא $\omega ^{\omega }+1$. על כל סודר מוגדרת טופולוגיה. למעשה תצוגה זאת מגדירה שיכון רציף של $\omega ^{\omega }+1$ למישור

66

דוגמה פופולרית בטופולוגיה: דפורמציה רציפה (הומוטופיה) בין ספל קפה וכעך שמדגימה כי שני הגופים הומיאומורפים, לשניהם טופולוגיה של טורוס. למעשה כדי ששני גופים יהיו הומיאומורפים אין צורך בדפורמציה רציפה, מספיק מיפוי והיפוך רציפים. המעבר בין הכעך לספל אינו אלא ארגון מחדש של הירעה מסביב לחור שבכעך בעזרת כיווץ ומתיחה מבלי לקרוע אותה או לחבר חלקים שלא היו מחוברים קודם.

67

פרוק פרדוקסלי של גרף קיילי של החבורה $F_{2}$ (החבורה החופשית עם 2 יוצרים). האנימציה מראה איך לפרק את הגרף למספר חלקים ולהרכיב מהם 2 העתקים של הגרף המקורי. פרוק כזה נקרא פרוק פרדוקסלי. בפני עצמו, פרוק זה אינו מפתיע יותר מהמלון של הילברט, אולם ניתן להסיק ממנו את משפט בנך-טרסקי (הנקרא לעתים פרדוקס בנך-טרסקי) הקובע כי קיים פרוק פרדוקסלי של הכדור.

68

ריצוף פנרוז, ריצוף כמו-מחזורי (קווזיפריאודי) בעזרת שני מעוינים שונים.

לריצוף זה סימטריה של שיקוף וסימטריה סיבובית מסדר חמש. על אף שניתן לזהות חזרה מקומית על קטעים מהריצוף, אין לו סימטריה של העתקה. רוג'ר פנרוז חקר מבנים אלה בשנות השבעים של המאה העשרים. מבנים כאלה מופיעים בגבישים כמו מחזוריים (קווזיגבישים) שנתגלו לראשונה על ידי פרופסור דן שכטמן מהטכניון ב-1982. התגלית הייתה פריצת דרך לגילוי גבישים חדשים ושימושים טכנולוגיים לתכונותיהם החדשות. פרופ' שכטמן זכה בעקבות התגלית בפרס נובל לכימיה בשנת 2011.

69

בעיית הדויגר-נלסון היא בעיה בקומבינטוריקה גאומטרית השואלת כמה צבעים צריך כדי לצבוע את המישור כך שאף שתי נקודות במרחק יחידה אחת מהשנייה לא יהיו צבועות באותו הצבע. בתמונה מודגם שאפשר לעשות זאת עם 7 צבעים. ניתן גם להראות כי 3 צבעים לא מספיקים, אך המספר המדויק עדין לא ידוע.

70

הכללה למשפט פיתגורס

ההכללה למשפט פיתגורס מוזכרת כבר ב"יסודות" של אוקלידס‏‏; אם על צלעותיו של משולש ישר-זווית מונחות צורות דומות, סכום השטחים שעל שני הניצבים שווה לשטח הצורה שעל היתר.

בצורה פורמלית יותר: אם על צלעות משולש ישר-זווית שאורכי צלעותיו הם $a,b,c\,$ בונים צורות ששטחיהן A,B,C כך ש ${\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}$, אזי A+B=C.

71

דיאגרמות דינקין הן אובייקט קומבינטורי הממין אובייקטים רבים מתחומים שונים במתמטיקה.

הדיאגרמות על גרסאותיהן השונות, ממיינות אלגבראות לי פשוטות (מעל המרוכבים), חבורות לי קומפקטיות פשוטות קשר (או לחלופין חסרות מרכז), חבורות קוקסטר, אלגבראות הקה, פאונים משוכללים, תת-חבורות סופיות של $SL_{2}(\mathbb {C} )$ (או $SO_{3}(\mathbb {R} )$), סינגולריות של יריעות אלגבריות דו-ממדיות ועוד.

ברוב המקרים אפשר לקשר בין האובייקטים גם בלי לעבור דרך דיאגרמות דינקין, אולם לעתים הקשר התגלה רק לאחר שהקשר לדיאגרמות דינקין היה ידוע. משפט בריסקורן אודות הקשר בין אלגבראות לי וסינגולריות של ירעות אלגבריות דו-ממדיות הוא דוגמה בולטת למקרה כזה.

72

דיאגרמת הביפורקציה של ההעתקה $x\mapsto rx(1-x)$ הדיאגרמה מציגה עבור כל ערך של $r$ את המסלולים המחזוריים היציבים (או באופן כללי יותר אטרקטורים) של המערכת הדינמית המוגדרת על ידי ההעתקה על הישר הממשי. מחקר של המערכת הדינמית המוגדרת על ידי העתקה זאת על המישור המרוכב הוא הבסיס להגדרתן של קבוצת מנדלברוט וקבוצת ג'וליה

73

פירמידת סרפינסקי היא אנלוג ממד גבוה של משולש סרפינסקי

פירמידת סרפינסקי היא פרקטל שנוצר על ידי הבניה הבאה: מכווצים פירמידה לחצי מגבוהה המקורי, ושמים חמש עותקים של פירמידה זו כך שקצותיהם נוגעות ואז חוזרים על התהליך.

תכונה של פירמידת סרפינסקי היא ששטח הפנים שלה אינסופי ואילו נפחה אפס.

74

הטורוס נוצר על ידי כפל שני המעגלים. אלו הם גם שני המעגלים הפשוטים על הטורוס. מעגלים אלו יחידים עד כדי הומוטופיה, והם יוצרים את ההומולוגיה הראשונה שלו ואת החבורה היסודית שלו.

75

פורטל:מתמטיקה/תמונה נבחרת/75

---

< בחזרה לפורטל