גליל (גאומטריה)

בגאומטריה, גָּלִיל הוא המקום הגאומטרי של כל הנקודות במרחב, הנמצאות במרחק קבוע, רדיוס הגליל, מישר כלשהו, ציר הגליל. זהו משטח אינסופי חלק, שהעקמומיות בכל נקודה על פניו קבועה. הגליל הוא משטח ישרים (עבור כל נקודה על פניו, קיים ישר העובר דרכה, ושוכן במשטח).
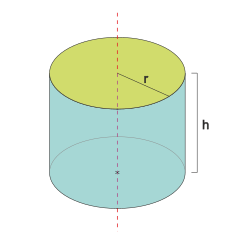
המושג גליל מתייחס גם לגוף הגאומטרי המוגבל על ידי המשטח הגלילי, ושני מישורים מקבילים החותכים אותו. כאשר המישורים החותכים מאונכים לציר, מתקבל גליל ישר. לגוף זה שטח פנים הבנוי ממשטח עקום, הקרוי מעטפת הגליל, ומשני עיגולים חופפים, התוחמים אותו משני צדדיו, הקרויים בסיסים. המרחק בין הבסיסים נקרא גובה הגליל. במקרה שבו המישורים החותכים אינם מאונכים למשטח, הצורה המתקבלת נקראת גליל לא ישר או גליל נטוי. במקרה זה, צורת הבסיסים היא של אליפסה, שצירה הקצר שווה באורכו לקוטר הגליל, וצירה הארוך גדל ביחס הפוך לקוסינוס זווית הנטייה של הגליל. גליל ישר הוא גם גוף סיבוב של מלבן המסובב סביב ציר העובר במרכז המלבן, ומקביל לשתיים מצלעותיו הנגדיות[1]. בהתאם להגדרה המכלילה של פאה, לגליל יש שלוש פאות.
תכונות גאומטריות
תכונותיו של גליל שרדיוסו וגובהו , הן
עבור נפח נתון, הגליל בעל שטח הפנים הקטן ביותר מקיים . בדומה, עבור שטח פנים נתון, הגליל בעל הנפח הגדול ביותר מקיים .
פריסה של גליל מעגלי ישר בנויה ממלבן, ושני עיגולים חופפים הצמודים לשניים מהניצבים הנגדיים שלו. המלבן הוא צורת מעטפת הגליל, לאחר ששוטחה, והעיגולים הם למעשה בסיסי הגליל השומרים על צורתם. כל אחד מהניצבים הצמודים לעיגולים שווה באורכו להיקף העיגול הצמוד אליו, ואורך שני הניצבים הנותרים שווה לגובה הגליל.

סוגי גליל אחרים

בגאומטריה דיפרנציאלית ניתנת למושג גליל הגדרה רחבה יותר: גליל הוא כל משטח ישרים הבנוי כולו מישרים מקבילים. מישור המאונך לאחד מישרי המשטח, בהכרח יהיה מאונך לשאר הישרים, וצורת החתך של המישור עם המשטח, מאפיינת למעשה את המשטח כולו. כך למשל, משטח שצורת החתך שלו היא אליפסה, נקרא גליל אליפטי. הקואורדינטות הקרטזיות של גליל זה הן:
ו- הם אורכי מחצית צירי האליפסה. כאשר שווה ל- מתקבל גליל מעגלי. בהתאם להגדרה זו, גליל יכול להיות משטח, שצורת החתך שלו היא לאו דווקא סגורה. דוגמאות לכך הם הגליל הפרבולי והגליל ההיפרבולי.
קישורים חיצוניים
- גליל, באתר אנציקלופדיה בריטניקה (באנגלית)
- גליל, באתר MathWorld (באנגלית)
הערות שוליים

- ↑ גליל הוא גם משטח סיבוב של קו ישר, המסובב סביב קו ישר אחר, המקביל לו
גליל (גאומטריה)39372979Q34132


