משפט ארבעת הצבעים
משפט ארבעת הצבעים הוא תוצאה בולטת בהיסטוריה של הטופולוגיה הקומבינטורית ושל תורת הגרפים. לפי המשפט, אפשר לצבוע כל מפה מדינית, באופן שכל שתי מדינות בעלות קו גבול משותף נצבעות בצבע שונה, תוך שימוש בארבעה צבעים לכל היותר. מתמטיקאים החלו לחקור את הבעיה באמצע המאה ה-19. היא נודעה כ'השערת ארבעת הצבעים', וזכתה להוכחות שגויות רבות.
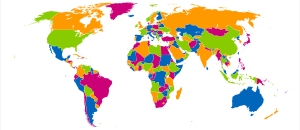
בניסוח מודרני, המשפט מבטיח שלכל גרף מישורי קיימת צביעת קודקודים בארבעה צבעים. אנשי תורת הגרפים מכירים הוכחות קלות יחסית לכך שקיימת צביעה בחמישה צבעים, אבל ההוכחה לכך שאפשר להסתפק בארבעה נמצאה רק ב-1976, והיא כרוכה בחיפוש ממוחשב על-פני אלפי מקרים. זו הייתה ההשערה המפורסמת הראשונה שהוכחה בעזרת מחשב, ובתחילה לא הייתה הסכמה כללית על תקפות ההוכחה, בעיקר בנימוק שלא הוכחה נכונותן של תוכניות המחשב עצמן. מאז נעשו ניסיונות רבים למצוא הוכחה סטנדרטית יותר, שיכולה לעמוד לביקורת עמיתים ללא עזרת מחשב. הוכחה כזו עדיין לא נמצאה.
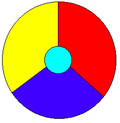
האיור משמאל מציג מפה סכמטית של ארבע מדינות, שלכל אחת מהן יש גבול משותף עם כל האחרות. לכן לא ניתן לצבוע אותה בפחות מארבעה צבעים.
מפות וגרפים
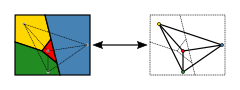
הקשר בין מפות מישוריות לבין גרפים מישוריים מבוסס על בניית הגרף הדואלי, שהיא בנייה סטנדרטית בתורת הגרפים. בגרף המתאים למפה נתונה, כל מדינה מיוצגת על ידי קודקוד, וכל שתי מדינות שלהן יש גבול משותף מחוברות בקשת בין שני הקודקודים המתאימים. משמאל מוצגת דוגמה למפה ולגרף המתאים לה.
כעת, צביעת המדינות על המפה שקולה לבחירת צבע לכל קודקוד, באופן כזה שלשני קודקודים המחוברים בקשת יש צבעים שונים. צביעה כזו של הגרף נקראת צביעת קודקודים.
היסטוריה
בעבר היה מקובל לחשוב שמשפט ארבעת הצבעים היה ידוע לקרטוגרפים, אך נראה שלטענה זו אין בסיס. ככל הידוע לנו היום, הטענה עלתה בדעתו של פרנסיס גאת'רי (Francis Guthrie) בשנת 1852, בעת שעסק בצביעת מפה של מחוזות אנגליה. לאחר שניסה למצוא הוכחה במשך זמן מה, הוא סיפר על הבעיה לאחיו פרדריק, שלמד אצל המתמטיקאי אוגוסטוס דה-מורגן. דה-מורגן ניסה בלא הצלחה לעניין בנושא מתמטיקאים אחרים, עד שב-1878 הובאה הבעיה לתשומת לבו של ארתור קיילי, שהציג אותה בפני החברה המלכותית הבריטית.
'הוכחה' ראשונה להשערת ארבעת הצבעים פורסמה לראשונה בשנת 1879, על ידי אלפרד קמפ (Kempe). קמפ הציע שיטה המבוססת על שרשראות של מדינות סמוכות, שאמורה הייתה לאפשר הוספה של מדינה אחר מדינה למפה הצבועה, מבלי להזדקק לצבע חמישי. ההוכחה נבדקה, והתקבלה על-דעת בני זמנו. ואולם, 11 שנה מאוחר יותר הראה פרסי ג'ון היווד (Heawood) שההוכחה אינה נכונה. בנוסף, היווד הראה שחמישה צבעים מספיקים לצביעת כל מפה.
השקילות לצביעת קשתות של גרפים מדרגה 3
במסגרת ניסיונו להוכיח את המשפט, הפיזיקאי הבריטי פיטר טייט (אנ')[1] הוכיח שצביעת מפות בארבעה צבעים שקולה לטענה הבאה: לכל גרף 3-רגולרי מישורי 2-קשיר-קשתות (כלומר, כזה שנשאר קשיר גם לאחר מחיקת אחת הקשתות) יש צביעת קשתות (כלומר, התאמה של צבע לכל קשת באופן ששתי קשתות נפגשות מקבלות צבעים שונים) בשלושה צבעים.[2]
הכללות
משפט ארבעת הצבעים עוסק, כאמור, בצביעה של מפות על פני המישור. קל לראות שמשימה זו שקולה לצביעה של מפה כדורית, שגם עבורה מספיקים ארבעה צבעים. עם זאת, טופולוגיים עסקו גם בשאלה כמה צבעים נחוצים למפה המצוירת על-פני משטחים אחרים, כגון טורוס או בקבוק קליין. את המשטחים הרלוונטיים (שהם משטחים חלקים קומפקטיים) אפשר למיין לפי שתי תכונות: מספר הצדדים של המשטח (אחד, כמו במקרה של בקבוק קליין, או שניים, כמו לכדור ולטורוס) ומאפיין אוילר , שאותו אפשר לחשב ממספר ה'חורים' במשטח (לכדור ולבקבוק קליין אין חורים, לטורוס יש אחד).
במאמרו מ-1890 הראה היווד שבכל משטח למעט הכדור, מספר הצבעים הדרוש אינו עולה על . בפרט, הטורוס ובקבוק קליין (בשניהם ) דורשים שבעה צבעים לכל היותר. ב-1934 הראה פיליפ פרנקלין (אנ') שעל-פני בקבוק קליין מספיקים שישה צבעים, וב-1959 הראה גרהרד רינגל (אנ') שבכל מקרה אחר החסם של היווד הוא מדויק.
הוכחת משפט ארבעת הצבעים
בשנת 1976 נעזרו וולפגאנג האקן וקנת אפל מאוניברסיטת אילינוי באורבנה-שמפיין בשרשראות של קמפ, כדי להראות שקיימת משפחה סופית של מפות (בהוכחה המקורית - 1936 מפות), שאם אפשר לצבוע את כולן, אז אפשר לצבוע בארבעה צבעים כל מפה אפשרית. הבדיקה שאכן מדובר במשפחה כזו דרשה חישוב מפורט ועתיר הסתעפויות, שנמשך (במחשבים של אותה תקופה) כ-1200 שעות. בשנת 1996 ניתנה הוכחה בעלת אופי דומה על ידי ניל רוברטסון, דניאל פ. סנדרס, פול סימור ורובין תומאס שבה היה די בבדיקה של 633 מפות. גם בדיקה זו דרשה הסתייעות במחשב.[3] רוברטסון וחבריו אף מצאו אלגוריתם ריבועי (שזמן הריצה שלו פרופורציוני לריבוע מספר הקודקודים) לצביעת גרף מישורי בארבעה צבעים.[4]
ראו גם
לקריאה נוספת
- קנת' אפל וולפגאנג הייגן The Solution of the Four-Color-Map Problem, Scientific American, גיליון 237, מס. 4, עמ' 108-121 (1977)
- Invitation to Combinatorial Topology, קיי פאן ומוריס, 1946, מלווה בהערות מאת הווארד איבס, 1967.
- סיימון סינג, המשפט האחרון של פרמה, הוצאת ידיעות אחרונות, 2000. עמ' 356–368.
- איאן סטיוארט, תיבת האוצרות המתמטיים של פרופסור סטיוארט, כנרת זמורה-ביתן דביר, 2012, הפרק "משפט ארבעת הצבעים", עמ' 22–29.
קישורים חיצוניים
- גדי אלכסנדרוביץ', משפט ארבעת הצבעים, באתר "לא מדויק"
- משפט ארבעת הצבעים, באתר MathWorld (באנגלית)
- סקירת בעיית ארבעת הצבעים ב-MacTutor (באנגלית)
- משפט ארבעת הצבעים, באתר אנציקלופדיה למתמטיקה (באנגלית)
- הוכחה חדשה למשפט ארבעת הצבעים (באנגלית)
- משפט ארבעת הצבעים, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים
- ↑ Blanuˇsa Double
- ↑ Louis H. Kauffman, Reformulating the map color theorem, Discrete Mathematics, Volume 302, Issues 1-3, 28 October 2005, Pages 145-172,
- ↑ The Four Color Theorem, School of Mathematics, באתר Georgia Tech, 8 בנובמבר 2007
- ↑ N. Robertson, D. P. Sanders, P. D. Seymour & R. Thomas, Efficiently four-coloring planar graphs, Proceedings of the ACM Symposium on the Theory of Computing, 28 (1996), 571-575.
משפט ארבעת הצבעים35197589Q184410


