יריעה אלגברית

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

שלישונית מפותלת. יריעה אלגברית (אפינית) חד-ממדית המתקבלת מחיתוך של שתי יריעות אלגבריות דו-ממדיות במרחב אפיני תלת-ממדי

יריעות אלגבריות (ובאופן כללי יותר סכמות) הן אובייקט המחקר המרכזי בגאומטריה אלגברית. באופן אינטואיטיבי, יריעה אלגברית היא אובייקט גאומטרי שנראה מקומית כמו יריעה אלגברית אפינית (זאת אומרת קבוצת אפסים של מערכת משוואות פולינומית במספר משתנים). בדומה למרחב וקטורי, יריעות אלגבריות מוגדרות תמיד מעל שדה $k$. בדרך כלל $k$ סגור אלגברית.

רקע

יריעות אפיניות

אליפסה - יריעה אלגברית אפינית חד־ממדית במישור המוגדת על ידי המשוואה ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

ערך מורחב – יריעה אלגברית אפינית

בגישה הקלאסית, יריעה אלגברית אפינית הוגדרה כקבוצת כל האפסים של משפחת פולינומים מעל שדה סגור אלגברית $k$. כלומר: אם $f_{1},...,f_{m}$ הם קבוצת פולינומים ב-$n$ משתנים (כלומר: $f_{i}(X_{1},...,X_{n})$ אזי היריעה האפינית המוגדרת על ידם היא

${\mathcal {V}}(f_{1},...,f_{n})=\left\{(x_{1},...,x_{n})\in k^{n}\mid \forall i:f_{i}(x_{1},...,x_{n})=0\right\}$.

באופן יותר מדויק, מסתכלים על המרחב האפיני $\mathbb {A} ^{n}:=k^{n}$ כמרחב ה-$n$-יות של מספרים משדה $k$ כאשר שוכחים את המבנה הטבעי של מרחב וקטורי שיש ל-$k^{n}$. על מרחב זה מגדירים k-אלגברה של פונקציות רגולריות מ-$\mathbb {A} ^{n}$ ל-$k$. במקרה האפיני פונקציות רגולריות אלה הן פולינומים ב-$n$ משתנים. כלומר: $k[\mathbb {A} ^{n}]=k[X_{1},...,X_{n}]$. נשים לב ש-k-אלגברה זו היא חוג נתרי לפי משפט הבסיס של הילברט, דבר המבטיח שהיא מקיימת מספר תכונות שימושיות, למשל: כל אידיאל בה הוא נוצר-סופית. על המרחב $\mathbb {A} ^{n}$ מגדירים טופולוגיית זריצקי (על שם אוסקר זריצקי) ההופכת אותו למרחב נתרי. בטופולוגיה זו כל הקבוצות הסגורות הן בדיוק הקבוצות מהצורה $S={\mathcal {V}}(I)$ באשר $I$ הוא אידיאל ב-$k[\mathbb {A} ^{n}]$. מאחר ש-$k[\mathbb {A} ^{n}]$ היא אלגברה נתרית $I$ נוצר סופית ולכן יש מספר סופי של פולינומים $f_{1},...,f_{m}$ היוצרים את $I$. כמו כן מתקיים ${\mathcal {V}}(I)={\mathcal {V}}(f_{1},...,f_{m})$, ולכן כל הקבוצות הסגורות הן בעצם קבוצות האפסים המשותפים של משפחות סופיות של פולינומים. לקבוצות כאלה קוראים "קבוצות אלגבריות".

תהי $S={\mathcal {V}}(I)$ קבוצה אלגברית. אזי חוג הפונקציות הרגולריות עליה ניתן על ידי $k[S]=k[\mathbb {A} ^{n}]/I$. אם $I$ אידיאל ראשוני אז $S$ היא יריעה אפינית אי-פריקה בטופולוגיית זריצקי. יריעה אי-פריקה היא יריעה שאי-אפשר להציגה כאיחוד של שתי תת-קבוצות סגורות החלקיות ממש ליריעה.

נשים לב שעבור יריעות אפיניות $X$ החוג של הפונקציות הרגולריות

$k[X]=\left\{f:X\to k\mid \ f{\mbox{ is regular on }}X\right\}$

הוא k-אלגברה נוצרת-סופית ללא איברים נילפוטנטיים. משפט האפסים של הילברט נותן אפיון לקשר בין תת-יריעות סגורות של $X$ לאידיאלים של $k[X]$.

כל k-אלגברה נוצרת-סופית ללא איברים נילפוטנטיים $A$ היא החוג של הפונקציות הרגולריות של יריעה אלגברית מתאימה. מסמנים יריעה זאת $Spec(A)$ והיא מכונה הספקטרום של $A$. בתור קבוצה, יריעה זאת היא אוסף האידיאלים המקסימליים של $A$. קבוצה זאת מסומנת ב $Specm(A)$ ונקראת הספקטרום המקסימלי של $A$.

יריעות פרויקטיביות

משטח בוי. הטבעה אלגברית למחצה של המישור הפרויקטיבי הממשי למרחב

דאבל, משחק קלפים המבוסס על המישור הפרויקטיבי מעל השדה$\mathbb {F} _{7}$. כל קלף במשחק מייצג ישר במישור זה, וכל תמונה על הקלף מייצגת נקודה על הישר המתאים. במישור הפרויקטיבי, כל שני ישרים נחתכים תמיד בנקודה אחת, ולכן לכל שני קלפים יש בדיוק תמונה משותפת אחת

תמונה זו מוצגת במכלול בשימוש הוגן.
נשמח להחליפה בתמונה חופשית.

ערך מורחב – יריעה אלגברית פרויקטיבית

המרחב הפרויקטיבי מהווה הרחבה של המרחב האפיני, בה לכל ישר מוסיפים נקודה נוספת באינסוף. באופן פורמלי יותר, המרחב הפרויקטיבי ה-$n$-ממדי $\mathbb {P} ^{n}$ מעל $k$ הוא אוסף כל הישרים העוברים דרך הראשית במרחב האפיני $(n+1)$-ממדי $\mathbb {A} ^{n+1}$. אם בוחרים היפר מישור שלא עובר דרך ה-0 במרחב ב-$\mathbb {A} ^{n+1}$ אז כל נקודה בהיפר מישור זה נמצאת על ישר יחיד שעובר דרך הראשית. לכן אפשר לחשוב על היפר מישור זה כעל תת-קבוצה במרחב הפרויקטיבי. כמעט כל הנקודות של המרחב הפרויקטיבי נמצאות בקבוצה זאת. אלה שלא נמצאות בה הן גבולות של סדרות של נקודות שנמצאות בה אשר מתאימות לסדרות של נקודות בהיפר מישור ששואפות לאינסוף בכיוון של ישר מסוים. מכיוון שהיפר מישור ב-$\mathbb {A} ^{n+1}$ הוא מרחב אפיני $n$-ממדי אנו רואים שהמרחב הפרויקטיבי הוא מעין השלמה של המרחב האפיני.

בהינתן קבוצה $X\subset \mathbb {P} ^{n}$ ניתן להגדיר קבוצה ${\tilde {X}}\subset \mathbb {A} ^{n+1}$ המהווה את איחוד כל הישרים שהם איברי $X$. הקבוצה $X$ נקראת יריעה פרויקטיבית אם"ם ${\tilde {X}}$ היא יריעה אפינית. ניתן להגדיר טופולוגיה על $X$ באופן דומה להגדרת הטופולוגיה של זריצקי על יריעות אפיניות. גם טופולוגיה זאת נקראת הטופולוגיה של זריצקי.

אפשר לחשוב על יריעות פרויקטיביות כעל קומפקטיפיקציות של יריעות אפיניות. לדוגמה, אם $k=\mathbb {C}$ אז יריעות פרויקטיביות הן תמיד קומפקטיות (בטופולוגיה המרוכבת) בעוד שיריעות אפיניות אינסופיות לעולם אינן קומפקטיות (בטופולוגיה המרוכבת). מכיוון שכל יריעה אפינית $X$ ניתן לשכן במרחב אפיני $\mathbb {A} ^{n}$ ואת $\mathbb {A} ^{n}$ ניתן לשכן במרחב הפרויקטיבי $\mathbb {P} ^{n}$, ניתן לשכן את $X$ ב-$\mathbb {P} ^{n}$. שיכון זה אינו סגור. אולם אפשר לקחת את הסגור זריצקי ${\bar {X}}$ של $X$ בתוך $\mathbb {P} ^{n}$ וכך לקבל יריעה פרויקטיבית המכילה את $X$ בתור קבוצה פתוחה צפופה.

הקומפקטיות של יריעות פרויקטיביות נותנת להם תכונות טובות יותר, ובמקרים רבים קל יותר לחקור אותם. הסיבה היא שבעוד שבמרחב האפיני דברים יכולים "לברוח לאינסוף", זה בלתי אפשרי במרחב הפרויקטיבי, כך שניסוחים של משפטים הופכים יותר פשוטים. לדוגמה במישור האפיני, שני ישרים שונים יכולים להחתך ב-0 או ב-1 נקודות. בעוד שבמישור הפרויקטיבי שני ישרים שונים נחתכים בדיוק בנקודה 1. דוגמה נוספת היא שפרבולה אליפסה והיפרבולה נהיות איזומורפיות כאשר סוגרים אותן במישור הפרויקטיבי. הסיבה להבדלים ביניהן במישור האפיני היא שאליפסה לא חותכת את האינסוף כלל, פרבולה חותכת אותו בנקודה אחת והיפרבולה ב-2. אם עובדים מעל המספרים המרוכבים ולא הממשיים אז דוגמה זאת מאבדת מעט מערכה מכיוון שאליפסה והיפרבולה איזומורפיות גם כיריעות מרוכבות אפינייות.

לא ניתן לחקור יריעה פורויקטיביות $X$ באמצעות חוג פונקציות הרגולריות עליהם, מכיוון שחוג זה קטן מאוד (אם היריעה קשירה או בלתי פריקה אז חוג זה הוא השדה $k$). את תפקידו של חוג זה תופס חוג הפונקציות הרגולריות על היריעה האפינית ${\tilde {X}}$. מכיוון שיריעה זאת אינווריאנטית להומותטיה (ז"א כפל בסקלרים מ-$k$), חוג הפונקציות עליה הוא חוג מדורג: פונקציה הומוגנית ממעלה $i$ על ${\tilde {X}}$ היא פונקציה המתקבלת מצימצום של פולינום הומוגני ממעלה $i$ על המרחב האפיני $\mathbb {A} ^{n+1}$. הקשר בין יריעות פרויקטיביות לאלגבראות מדורגות דומה לקשר בין יריעות אפיניות לאלגבראות.

מכיוון שניתן לכסות את $\mathbb {P} ^{n}$ על ידי $n+1$ העתקים של $\mathbb {A} ^{n}$ (המתאימים ל-$n+1$ היפר מישורים ב-$\mathbb {A} ^{n+1}$) ניתן גם לכסות כל יריעה פרויקטיבית על ידי מספר סופי של יריעות אפיניות. כיסוי כזה מאפשר דרך נוספת לחקור יריעות פרויקטיביות.

יריעות קוואזי-אפיניות וקוואזי-פרויקטיביות

ערכים מורחבים – יריעה קוואזי-אפינית, יריעה קוואזי-פרויקטיבית

קבוצה פתוחה ביריעה אפינית $X$ הנתונה על ידי התנאי $f(x)\neq 0$ כאשר $f$ היא פונקציה רגולרית על $X$ נקראת קבוצה פתוחה בסיסית. על קבוצה כזאת יש מבנה טבעי של יריעה אפינית מכיוון שאפשר לשכן אותה כקבוצה סגורה ב-$X\times \mathbb {A} ^{1}$:

$$\{(x,\alpha )\in X\times \mathbb {A} ^{1}|\alpha f(x)=1\}$$

אולם לא ניתן לבצע זאת עבור קבוצות פתוחות כלליות. לדוגמה על הקבוצה $\mathbb {A} ^{2}\smallsetminus 0$ אין מבנה של יריעה אפינית. קבוצה פתוחה ביריעה אפינית נקראת יריעה קוואזי-אפינית. ניתן לחקור יריעות קוואזי-אפיניות על ידי היריעות האפיניות המכילות אותן או על ידי הקבוצות הבסיסיות המכסות אותן (שהן גם כן יריעות אפיניות).

באופן דומה יריעה קוואזי-פרויקטיבית היא קבוצה פתוחה ביריעה פרויקטיבית. נשים לב שכל יריעה אפינית היא קוואזי-פרויקטיבית (מכיוון שאפשר לשכן מרחב אפיני בתור קבוצה פתוחה במרחב פרויקטיבי).

יריעות קוואזי-פרויקטיביות מהוות מחלקה רחבה של אובייקטים גאומטריים. תתי-קבוצות פתוחות וסגורות ביריעות קוואזי-פרויקטיביות הן יריעות קוואזי-פרויקטיביות. גם היום כאשר המושג של יריעה אלגברית כללית ידוע ומקובל היטב, חלק גדול מהמחקר בגאומטריה אלגברית מתמקד ביריעות קוואזי-פרויקטיביות.

למעשה לא קל למצוא דוגמה של יריעה אלגברית שאיננה קוואזי-פרויקטיבית. המוטיבציה של וייל להגדיר את המושג הכללי של יריעה אלגברית באה מדוגמה מסוימת, אולם דוגמה זאת התבררה לימים כיריעה קוואזי-פרויקטיבית (אם כי מסיבות לא טריוויאליות). דוגמה ליריעה אלגברית לא קוואזי-פרויקטיבית נמצאה רק לאחר כעשור על ידי נגטה.

בדומה ליריעות פרויקטיביות ויריעות קוואזי-אפינית גם יריעות קוואזי-פרויקטיביות ניתן לכסות על ידי מספר סופי של קבוצות פתוחות המהוות יריעות אפיניות.

מגבלות של יריעות קוואזי-פרויקטיביות

למרות המגוון הרחב של יריעות קוואזי-פרויקטיביות יש להן מגבלות רבות. ראשית, הצורך לקבוע שיכון למרחב פרויקטיבי על מנת לדבר על היריעה איננו טבעי. ברמה היותר פרקטית, מסובך לבצע בנייות גאומטריות בסיסיות עם יריעות קוואזי-פרויקטיביות, ולעיתים אף בלתי אפשרי. לדוגמה לא ברור איך להגדיר מבנה של יריעה (קוואזי) פרויקטיבית על מכפלה קרטזית של יריעות (קוואזי) פרויקטיביות. הדבר ניתן לביצוע על ידי שיכון של מכפלה של מרחבים פרויקטיבים למרחב פרויקטיבי, הנקרא שיכון סגרה, אך פתרון זה איננו טריוויאלי, ומעלה משמעותית את ממד המרחב הפרויקטיבי אליו משוכנת היריעה. דוגמה נוספת היא פעולת ההדבקה. בהינתן שני מרחבים טופולוגיים $X$ ו-$Y$ ושיכונים פתוחים $i_{1}:U\to X$ ו-$i_{2}:U\to Y$ ניתן להגדיר את ההדבקה $X\sqcup _{U}Y$ לאורך $U$ בתור האיחוד הלא קשיר $X\sqcup Y$ מודולו יחס השקילות $i_{1}(x)\sim i_{2}(x)$. פעולה זאת אינה ניתנת לביצוע ליריעות קוואזי-פרויקטיביות. הצורך בביצוע פעולה זאת מהווה את המוטיבציה המרכזית להגדרה המודרנית של יריעה אלגברית.

הגדרה פורמלית באמצעות אלומת פונקציות

באופן אינטואיטיבי, ניתן להגדיר יריעה אלגברית כללית בתור "תוצר ההדבקה של מספר יריעות אפיניות". ברמה הפורמלית יש להגדיר מחלקה רחבה יותר של אובייקטים גאומטריים שיריעות אלגבריות מהוות חלק ממנה, ולהגדיר את ההדבקה במחלקה זאת. ישנן מספר מחלקות כאלה. אחת הפופולרית בהן היא "אוסף המרחבים הטופולוגיים עם אלומות פונקציות".

מרחב עם אלומת פונקציות

יהי $X$ מרחב טופולוגי. אלומת פונקציות ${\mathcal {O}}$ (עם ערכים ב $k$) על $X$ היא התאמה אשר מתאימה עבור כל קבוצה פתוחה $U\subset X$, תת-אלגברה ${\mathcal {O}}(U)$ (עם יחידה) של אלגברת הפונקציות מ-$U$ ל-$k$, כך שמתקיים:

• לכל קבוצה פתוחה $V\subset U$, אם $f\in {\mathcal {O}}(U)$ אז הצמצום $f|_{V}$ של $f$ ל-$V$ שיך ל-${\mathcal {O}}(V)$
• לכל כיסוי פתוח $U=\bigcup V_{i}$, אם $f|_{V_{i}}\in {\mathcal {O}}(U)$ אז $f\in {\mathcal {O}}(U)$

אם $U\subset X$ קבוצה פתוחה אז ניתן להגדיר את הצמצום ${\mathcal {O}}|_{U}$ של ${\mathcal {O}}$ ל-$X$ על ידי ${\mathcal {O}}|_{U}(V):={\mathcal {O}}(V)$, לכול קבוצה פתוחה $V\subset U$.

זוג $(X,{\mathcal {O}})$ המורכב ממרחב טופולוגי $X$ ואלומת פונקציות ${\mathcal {O}}$ עליו, נקרא מרחב עם אלומת פונקציות. אם $(X,{\mathcal {O}})$ הוא מרחב עם אלומת פונקציות אז $O$ נקראת אלומת המבנה של $X$. יהיו $(X_{1},{\mathcal {O}}_{1})$ ו-$(X_{2},{\mathcal {O}}_{2})$ מרחבים עם אלומות פונקציות. העתקה $\phi :X\to Y$ נקראת מורפיזם של מרחבים עם אלומות פונקציות אם $\phi$ רציפה ולכל $U\subset Y$ ו-$f\in {\mathcal {O}}(U)$ מתקיים :$f\circ \phi \in {\mathcal {O}}(\phi ^{-1}(U))$.

אוסף המרחבים עם אלומות פונקציות הוא קטגוריה, בפרט שני מרחבים עם אלומות פונקציות $(X_{1},{\mathcal {O}}_{1})$ ו-$(X_{2},{\mathcal {O}}_{2})$ נקראים איזומורפיים אם קיימות העתקות $\phi :X\to Y$ ו-$\psi :Y\to X$ של מרחבים עם אלומות פונקציות כך ש: $\phi \circ \psi =\mathrm {Id} _{Y}$ ו $\psi \circ \phi =\mathrm {Id} _{X}$.

מרחבים עם אלומות פונקציות הם מקרים פרטיים של מרחבים מחויגים.

יריעות אפיניות כמרחב עם אלומת פונקציות

תהי $X$ יריעה אפינית. תהי $U\subset X$ קבוצה פתוחה. מכיוון ש-$U$ היא יריעה קוואזי-אפינית, ניתן להגדיר את חוג הפונקציות הרגולריות ${\mathcal {O}}$ על $U$. קל לראות שההתאמה $U\mapsto {\mathcal {O}}(U):=k[U]$ נותנת אלומת פונקציות. מכאן ש-$X$ מצוידת בטופולוגיה של זריצקי יחד עם אלומת הפונקציות הרגולריות ${\mathcal {O}}$ מהווה מרחב עם אלומת פונקציות. קל לראות כי העתקה $\phi :X\to Y$ היא מורפיזם של יריעות, אם"ם היא מורפיזם של מרחבים עם אלומות פונקציות. במילים אחרות קטגוריית היריעות האפיניות היא תת-קטגוריה מלאה בקטגוריית המרחבים עם אלומות פונקציות.

לא כל מרחב עם אלומת פונקציות הוא יריעה אפינית. יריעה אפינית $Y$ היא מרחב עם אלומת פונקציות שמקיים את התכונות הבאות:

1. חתך הפונקציות הרגולריות גלובלית על $Y$ שנסמנו $k[Y]:={\mathcal {O}}_{Y}$ הוא k-אלגברה נוצרת סופית.
2. ההעתקה $\ast :\mathrm {Mor} (X,Y)\to \mathrm {Hom} _{k}(k[Y],k[X])$ מקבוצת המורפיזמים של מרחבים עם אלומת פונקציות לקבוצת ההומומורפיזמים של k-אלגבראות ששולחת את $f:X\to Y$ ל-$f^{*}:k[Y]\to k[X]$ כאשר $f^{*}(g)=g\circ f$, היא חח"ע ועל (bijection) לכל מרחב עם אלומת פונקציות $X$.

הגדרה של יריעה אלגברית

מרחב עם אלומת פונקציות $(X,{\mathcal {O}})$ נקרא יריעה אלגברית אם קיים כיסוי פתוח סופי

$X=\bigcup _{i=1}^{n}U_{i}$

כך ש-$(U_{1},{\mathcal {O}}|_{U_{1}})$ איזומורפי (כמרחב עם אלומת פונקציות) ליריעה אלגברית אפינית. מורפיזם של יריעות מוגדר להיות מורפיזם של מרחבים עם אלומות פונקציות. הטופולוגיה על יריעה נקראת הטופולוגיה של זריצקי.

מורפיזם בין יריעות אלגבריות

מורפיזם של יריעות מוגדר בתור מורפיזם בין מרחבים עם אלומת פונקציות. במילים אחרות קטגורית היריעות האלגבריות מוגדרת להיות התת-קטגוריה המלאה של קטגורית המרחבים עם אלומות פונקציות, שהאובייקטים שלה הם יריעות אלגבריות.

פעולות עם יריעות

בניות קטגוריות

יש העתקה יחידה מהאובייקט התחילי (הקבוצה הריקה) לכל יריעה (אליפסה לדוגמה), והעתקה יחידה מכל יריעה לאובייקט הסופי (נקודה).

הישר הפרויקטיבי המתקבל מהדבקה של שני ישרים אפיניים. יש להדביק על פי החצים הכחולים

המישור - מהווה מכפלה קרטזית של שני ישרים

אוסף היריעות האלגבריות הוא קטגוריה. בקטגוריה זאת קיימים גבולות הפוכים סופיים, וגבולות ישרים מסוימים. בפרט ניתן להגדיר את הבניות הבאות:

• אובייקט תחילי - על הקבוצה הריקה יש מבנה יחיד של יריעה אלגברית
• אובייקט סופי - על קבוצת היחידון (ולמעשה על כל קבוצה סופית) יש מבנה יחיד של יריעה אלגברית
• קו-מכפלה - עבור 2 יריעות אלגבריות $X$ ו-$Y$ ניתן להגדיר מבנה טבעי של יריעה אלגברית על האיחוד הלא קשיר $X\sqcup Y$ של $X$ ו-$Y$ באופן הבא:

$$f\in {\mathcal {O}}(U)\iff f|_{U\cap X}\in {\mathcal {O}}(U\cap X){\text{ and }}f|_{U\cap Y}\in {\mathcal {O}}(U\cap Y)$$

• pushout - באופן דומה אפשר להגדיר מבנה של יריעה על הדבקה של שתי יריעות לאורך תת-קבוצה פתוחה. ניתן גם להגדיר הדבקה של יריעוֹת לאורך תת-קבוצה סגורה.
• מכפלה - על המכפלה הקרטזית של שתי יריעות $X$ ו-$Y$ ניתן להגדיר מבנה של יריעה. עם זאת, טופולוגיית זריצקי על היריעה $X\times Y$ איננה טופולוגיית המכפלה של היריעה $X\times Y$. אם $X$ ו-$Y$ אפיניות אז ניתן להגדיר את מבנה היריעה (האפינית) על $X\times Y$ בקלות, למשל בהתבסס על השיכון למרחב אפיני. במקרה הכללי ניתן לכסות את $X$ ו-$Y$ על ידי יריעות אפיניות, ומכאן להגדיר את מבנה היריעה על $X\times Y$.
• מכפלת סיבים - יהיו $\phi :X\to S,\psi :Y\to S$ העתקות של יריעות אלגבריות. מכפלת הסיבים $X\times _{S}Y:=\{(x,y)\in X\times Y|\phi (x)=\psi (y)\}$ היא תת-קבוצה סגורה (זריצקי) במכפלה $X\times Y$ מכאן ניתן להגדיר עליה מבנה של יריעה.
• גבול הפוך - עבור כל דיאגרמה סופית ${\mathcal {D}}$ של יריעות אלגבריות ניתן לבטא את הגבול ההפוך על פי ${\mathcal {D}}$ באמצעות מכפלות סיבים ולכן הגבול קיים בקטגוריה של יריעות אלגבריות.

בניות אינפיניטסימליות

המרחב המשיק לספירה

בנוסף ניתן להגדיר בניות רבות המוגדרות עבור יריעות חלקות בטופולוגיה דיפרנציאלית וגאומטריה דיפרנציאלית עבור יריעות אלגבריות. לדוגמה עבור יריעה אלגברית $X$ ונקודה $x\in X$ ניתן להגדיר את המרחב המשיק $T_{x}X$ ל-$X$ ב-$x$. מושג המרחב המשיק הוא מקומי. לכן די להגדירו עבור יריעה אפינית. במקרה זה $T_{x}X$ הוא המרחב הדואלי ל-${\mathfrak {m}}_{x}/{\mathfrak {m}}_{x}^{2}$, כאשר ${\mathfrak {m}}_{x}$ הוא אידיאל הפונקציות שמתאפסות ב-$x$.

ניפוח

ערך מורחב – ניפוח (גאומטריה אלגברית)

המחשה גאומטרית של הניפוח של המישור בנקודה. אפשר לחשוב על הניפוח הזה בתור הגרף של הפונקציה (הרב ערכית) הנתונה על ידי הנוסחה: $(x,y)\mapsto {\frac {y}{x}}$. העתקת הניפוח היא ההיטל של גרף זה על מישור ה- $(x,y)$ (שקוף). הישרים השחורים עוברים לישרים שונים במישור. הישר האדום עובר כלו ל-0. הוא נקרא הסיב המיוחד. התמונה חסומה בגובה. ובפרט לא רואים בה את ה־$\infty$ של הסיב המיוחד ואת הישר בו $z=\infty$ שעובר (תחת ההטיל) לציר ה- $y$

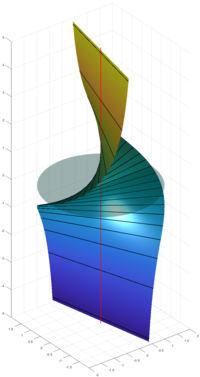
בנייה חשובה נוספת של יריעות אלגבריות היא הניפוח (blow-up). ניפוח של יריעה אלגברית $X$ לאורך תת-יריעה סגורה $Z$ היא בנייה מסוימת של יריעה ${\tilde {X}}$ ביחד עם העתקה נאותה ${\tilde {X}}\to X$ אשר מהווה איזומרפיזם מחוץ ל-$Z$. באופן אינטואיטיבי הניפוח מחליף את $Z$ בפרויקטיביזציה של האגד הנורמלי ל-$Z$. לניפוח חשיבות רבה בגאומטריה אלגברית, בין השאר מכיוון שהוא מהווה את הכלי המרכזי לבנית התרת סינגולריות.

מחלקות של יריעות והעתקות

אליפסה - יריעה אלגברית בלתי פריקה	שני קווים נחתכים - יריעה אלגברית פריקה אך קשירה
היפרבולה - יריעה אלגברית בלתי פריקה (ולכן גם קשירה) שקבוצת הנקודות הממשיות שלה איננה קשירה (ביחס לטופולוגיה הממשית)	שני קווים מקבילים - יריעה אלגברית לא קשירה (ולכן גם פריקה)
	יריעה לא פרידה המתקבלת מהדבקה של שני ישרים לאורך המשלים לראשית. יש להדביק לפי החצים הכחולים אך לא להדביק את הראשית (המסומנת בצלב אדום)
היפרבולואיד חד-יריעתי - דוגמה ליריעה חלקה	קונוס ריבועי - דוגמה ליריעה לא חלקה (סינגולרית). ליריעה זאת נקודה סינגולרית יחידה (ולכן מבודדת). הסינגולריות שלה היא חיתוך מלא ובפרט גורנשטין ובפרט כהן-מקולי. כמו כן היא סינגולריות סמפלקטית ובפרט רציונלית ובפרט נורמלית. עבור סינגולריות גורנשטין, הרציונליות שקולה לקנוניות ולכן היא גם קנונית ובפרט לוג קנונית.

תכונות טופולוגיות

טופולוגית זריצקי על יריעה אלגברית איננה משקפת את המבנה הגאומטרי של היריעה. למשל, היא כמעט לעולם אינה האוסדורפית ותמיד (קוואזי-) קומפקטית. לכן רוב המושגים מטופולוגיה (ובפרט מטופולוגיה אלגברית) לא יהיו רלוונטיים עבור יריעות אלגבריות, ובדרך כלל יהיה צורך להגדיר אנלוגים שלהם באמצעות שאר המבנה על יריעה אלגברית. עם זאת יש מספר מושגים בסיסיים שניתן להגדיר על ידי הטופולוגיה בלבד.

• יריעה אלגברית נקראת אי-פריקה (irreducible) אם היא אי-פריקה כמרחב טופולוגי, זאת-אומרת שלא ניתן להציגה כאיחוד של שתי קבוצות סגורות שאינן היריעה כולה.
• יריעה אלגברית נקראת קשירה אם היא קשירה כמרחב טופולוגי (ביחס לטופולוגיית זריצקי). בפרט כל ירעה קשירה היא בלתי פריקה.
• הממד של יריעה הוא ממד קרול שלה כמרחב טופולוגי, זאת-אומרת האורך המקסימלי של שרשרת עולה ממש של קבוצות סגורות אי-פריקות שאינן היריעה כולה.

תכונות גלובליות

שתי מחלקות בסיסיות של יריעות אלגברית הן יריעות פרידות ויריעות שלמות.

• יריעה $X$ נקראת פרידה אם האלכסון $\Delta X=\{(x,x)|x\in X\}$ הוא קבוצה סגורה (זריצקי) ב $X\times X$. מושג זה אנלוגי להאוסדורפיות. כל יריעה אפינית היא פרידה.
• יריעה $X$ נקראת שלמה אם לכל יריעה $Y$ ההטלה $p:X\times Y\to Y$ היא העתקה סגורה (זאת-אומרת שהיא מעבירה קבוצה סגורה לקבוצה סגורה). מושג זה אנלוגי לקומפקטיות. יריעה קואזי-פרויקטיבית היא פרידה אם"ם היא פרויקטיבית.

הערה: אם נחזור על הגדרות אלה עבור מרחבים טופולוגיים, נקבל הגדרות שקולות להאוסדורפיות וקומפקטיות. אולם מושגים אלה אינם שקולים להאוסדורפיות וקומפקטיות (לפי טופולגית זריצקי) מכיוון שטופולגיית המכפלה על $X\times Y$ שונה מהטופולגיה על $X\times Y$.

בנוסף יש עוד תכונות גלובליות רבות הנחקרות בגאמטריה אלגברית, למשל תכונות המבוססות על מושג השקילות הבירציונלית (כמו רציונליות) ותכונות המבוססות על אלומות קוהרנטיות (כמו Fano ו Calabi-Yau)

תכונות מקומיות

התכונה המקומית הבסיסית של יריעות אלגבריות היא חלקות. יריעה אלגברית $X$ נקראת חלקה בנקודה $x\in X$ אם ממד המרחב המשיק $T_{x}X$ ל-$X$ בנקודה $x$ שווה לממד היריעה $X$ בנקודה $x$. יריעות אלגבריות חלקות דומות מאוד למרחב אפיני באופן מקומי, אף על פי שאין איזומורפיזם בין סביבת זריצקי של נקודה חלקה לקבוצה פתוחה במרחב אפיני. לכן כאשר חוקרים את המבנה המקומי של יריעה אלגברית מתעניינים בדרך כלל ביריעות סינגולריות (זאת-אומרת לא חלקות) ומחקר זה נקרא תורת הסינגולריות. בין התכונות השונות של סינגולריות אפשר למנות: נורמליות, כהן-מקולי, גורנשטין, חיתוך מלא, מחלק עם חיתוך נורמלי, סינגולריות רציונלית, סינגולריות (לוג) קנונית, סינגולריות (לוג) טרמינאלית, סינגולריות סמפלקטית ועוד.

העתקות ומשפחות של יריעות

אחת הדרכים לחשוב על העתקה בין יריעות אלגבריות $\phi :X\to Y$ היא בתור משפחה של יריעות אלגבריות, כאשר הפרמטר של המשפחה היא נקודה שנעה ב-$X$, ולכל נקודה $x\in X$ אנו מתאימים את היריעה $\phi ^{-1}(x)$. לפי הגישה היחסית של גרותנדיק אפשר לנסות להכליל כל מושג שהוגדר עבור יריעות אלגבריות, גם עבור משפחה של יריעות אלגבריות או במילים אחרות - העתקות. בצורה זאת ניתן להגדיר את המושגים הבאים:

• העתקה אפינית
• העתקה פרויקטיבית
• העתקה פרידה
• העתקה נאותה (הגרסה היחסית של יריעה שלמה)
• העתקה חלקה (גרסה יחסית של יריעה חלקה; המושג בגאומטריה אלגברית המקביל לסובמרסיה מטופולוגיה דיפרנציאלית)

תכונות אלו הן בעצם תכונות של משפחות של יריעות יותר משהן תכונות של העתקות. תכונות כאלה תמיד מקומיות (על פי הטווח). יש גם תכונות מקומיות שאין להן גרסה מובהקת עבור יריעה, למשל, העתקה סופית, העתקה קוואזי-סופית, העתקת אטל, העתקה שטוחה ושקילות בירציונלית (על שלוש הדוגמאות הראשונות אפשר לחשוב כעל גרסאות יחסיות שונות של יריעות סופיות).

מערכות מונחים שונות

מבחינה היסטורית נלמדו תחילה יריעות אפיניות אז יריעות פרויקטיביות אחריהן יריעות קוואזי-פרויקטיביות ולבסוף יריעות כללית, שהוגדרו זמן קצר לפני סכמות שהן הכללה מרחיקת לכת של יריעות. לפני שנוסחה ההגדרה המודרנית של יריעה, המילה יריעה התייחסה רק ליריעות קוואזי-פרויקטיביות, עד היום ישנם ספרים שמשתמשים בשם יריעות רק עבור יריעות קוואזי-פרויקטיביות ודנים בשאר היריעות במסגרת דיון כללי יותר על סכמות. רוב המקורות משתמשים במילה יריעות במובן רחב יתר אך לפעמים מוסיפים מגבלות מסוימות. במקרים רבים דורשים מיריעה להיות פרידה ולעיתים גם בלתי פריקה.

מאידך לעיתים המושג יריעות אלגבריות כולל גם יריעות מעל שדות לא סגורים אלגברית. במקרה כזה ההגדרה למעלה לא תקפה כיוון שיש מערכות משוואות פולינומיות ללא פתרונות מעל שדה לא סגור אלגברית $k$ שהיריעה שהם מגדירים אינה ריקה. לדוגמה המשוואה $x^{2}+1=0$ מגדירה יריעה לא ריקה מעל $\mathbb {R}$ אולם אין לה פתרונות מעל $\mathbb {R}$. יש מספר הגדרות אלטרנטיביות שתקפות לשדות לא סגורים אלגברית (ראה להלן) אך בדרך כלל מטפלים במקרה זה במסגרת כללית יתר של סכמות.

מונחים בשפות שונות

באנגלית יריעה אלגברית נקראת "algebraic variety". בעברית וגם ברוסית, המילה "יריעה" משמשת גם לתיאור יריעה טופולוגית ובפרט יריעה חלקה, שבאנגלית נקראת "manifold". במקרים רבים יריעה אלגברית היא גם יריעה חלקה, אך יש לזכור שמדובר בשתי קטגוריות שונות זו מזו.

נקודות של יריעה

לפי ההגדרה שמופיעה למעלה יריעה אלגברית היא קבוצה עם מספר מבנים נוספים (טופולוגיה ואלומת פונקציות). לקבוצה זאת קוראים לעיתים קבוצת ה-$k$-נקודות של היריעה, כאשר $k$ הוא השדה מעליו מוגדרת היריעה. מסמנים קבוצה זאת $X(k)$.

הצורך להפריד בין יריעה $X$ לקבוצה $X(k)$ מגיע מהמקרה של יריעות המוגדרות מעל שדות לא סגורים אלגברית (או באופן כללי יתר סכמות), במקרה זה ההגדרה של יריעה אלגברית שונה, והקשר בין היריעה לקבוצת הנקודות שלה חלש יותר. לדוגמה היריעה המוגדרת על ידי המשוואה $x^{2}+1=0$ לא ריקה אך קבוצת ה-$\mathbb {R}$-נקודות שלה ריקה.

בנוסף, הפרדה זאת מאפשרת להגדיר מבנים נוספים על הקבוצה $X(k)$ שאינם מתואמים עם המבנים על היריעה $X$ (הטופולוגיה ואלומת הפונקציות). למשל, אם השדה $k$ הוא שדה טופולוגי אז ניתן להגדיר טופולוגיה מתאימה על קבוצת ה-$k$-נקודות של היריעה. טופולוגיה זאת תהיה בדרך כלל חזקה יותר מהטופולגיה של זריצקי. במקרה שהיריעה היא אפינית טופולוגיה זאת מוגדרת להיות הטופולוגיה המושרית מ-$k^{n}$ (קל לראות שהטופולוגיה לא תלויה בצורה שאנו מציגים את היריעה בתור קבוצה סגורה זריצקי ב-$k^{n}$). ליריעה כללית $X$ קבוצה $V\subset X(k)$ נקראת פתוחה אם לכל קבוצה פתוחה אפינית $U\subset X$ הקבוצה $U(k)\cap V$ פתוחה ב $U(k)$.

ניתן גם להגדיר באופן דומה את הקבוצה $X(R)$ של $R$ נקודות כאשר $R$ הוא $k$-אלגברה (קמוטטיבית עם יחידה) כלשהי.

קשר עם יריעות אנליטיות וחלקות

ערכים מורחבים – יריעה אנליטית, יריעה חלקה

אם $X$ היא יריעה אלגברית חלקה המוגדרת מעל שדה המספרים המרוכבים $\mathbb {C}$ אז ניתן להגדיר על קבוצת הנקודות שלה, $X(\mathbb {C} )$, מבנה של יריעה חלקה באופן הבא: במקרה ש-$X\subset \mathbb {A} ^{n}$ היא יריעה אפינית חלקה אז קל לראות ש $X(\mathbb {C} )\subset \mathbb {C} ^{n}$ היא תת-יריעה חלקה של $\mathbb {C} ^{n}$. במקרה הכללי בוחרים כיסוי פתוח של $X$ על ידי יריעות אפיניות, והוא מגדיר אטלס חלק.

באופן דומה, אם $X$ היא יריעה אלגברית המוגדרת מעל $\mathbb {C}$ אז ניתן להגדיר על $X(\mathbb {C} )$, מבנה של יריעה אנליטית.

בניות דומות קימות גם לשדות לא סגורים אלגברית. בפרט אם $X$ היא יריעה אלגברית חלקה המוגדרת מעל שדה המספרים הממשיים $\mathbb {R}$ אז ניתן להגדיר על $X(\mathbb {R} )$ מבנה של יריעה חלקה. כמו כן אם $X$ היא יריעה אלגברית המוגדרת מעל שדה מקומי $F$ אז ניתן להגדיר על $X(F)$ מבנה של יריעה אנליטית מעל $F$.

אגדים

ערך מורחב – אגד וקטורי

בדומה למרחבים טופולוגיים ויריעות דיפרנציאבילות, המושג אגד קיים גם על יריעות אלגבריות. ניתן להגדיר אגד על יריעה אלגברית $X$ בתור יריעה אלגברית $E$, יחד עם מורפיזם $p:X\to E$ ומבנה של מרחב וקטורי על הסיב $p^{-1}(x)$ של כל נקודה $x\in X$ כך שמקומית (בטופולוגיית זריצקי) מבנה זה איזומורפי ל $X\times V\to X$ כאשר $V$ הוא מרחב ליניארי.

לאגדים בגאומטריה אלגברית יש אותם תפקידים כמו לאגדים בטופולוגיה דיפרנציאלית. בפרט, עבור יריעה אלגברית חלקה ניתן להגדיר את האגד המשיק ואגדים קשורים אליו (אגד קו-משיק, אגד התבניות הדיפרנציאליות, ועוד). ישנם מספר אגדים בטופולוגיה דיפרנציאלית שאין אגד על יריעות אלגבריות המהווה מושג מקביל להם, למשל אגד האוריינטציות ואגד הצפיפויות. זאת משום שהגדרה של אגדים אלה מתבססת על יחס הסדר ב-$\mathbb {R}$. בנוסף, בגאומטריה אלגברית יש חשיבות מיוחדת לאגדים חד־ממדיים. אלה נקראים אגדים קווים, ונחקרים בעיקר במונחים של אלומות קוהרנטיות (ראה להלן).

אלומות על יריעות

ערך מורחב – אלומה

אחד הכלים המרכזיים לחקר יריעות אלגבריות הוא חקר של סוגים שונים של אלומות עליהן. בין היתר, אלומות משמשות למטרות הבאות:

• חקר תכונות של פונקציות רציונליות (זאת אומרת פונקציה שהיא מנה של שתי פונקציות רגולריות) על יריעות. למשל במשפט רימן רוך.
• חקר משפחות של מרחבים ליניאריים הקשורים ליריעה, כמו המרחב המשיק.
• בנייה של יריעות חדשות, כמו האגד המשיק.
• חקר תכונות מקומיות או גלובליות של היריעה. למשל סינגולריות.
• חקר יחסים בין יריעות ותכונות של העתקות, למשל שטיחות.
• חקר אינווריאנטים אלגבריים של יריעות הדומים לאינווריאנטים הנחקרים בטופולוגיה אלגברית. למשל הומולוגיות $\ell$-אדיות, הדומות להומולוגיה סינגולרית.
• בניית מרחבים ליניאריים בעלי מבנה מעניין. כמו במשפט בורל-וייל-בוט או באינדוקצית דלין-לוסטיג.
• ספירת נקודות על יריעה מעל שדה סופי. במילים אחרות ספירת הפתרונות של מערכת משוואות פולינומיות כאשר המשתנים רצים בשדה סופי. דוגמה מרכזית לשימוש זה הוא בהוכחת השערות וייל
• בנייה וחקר פונקציות על יריעות. למשל אלומות הקרקטרים של לוסטיג מאפשרות לחקור קרקטרים של הצגות בלתי פריקות של חבורות סופיות.

אלומות קוהרנטיות וקוואזי-קוהרנטיות

ערכים מורחבים – אלומה קוהרנטית, אלומה קוואזי-קוהרנטית

הסוגים הבסיסיים של אלומות על יריעות אלגבריות הם אלומות קוהרנטיות וקוואזי-קוהרנטיות. על יריעה אפינית $X$ ניתן להגדיר אלומות קוואזי-קוהרנטיות באופן הבא: בהינתן מודול $M$ מעל $O(X)$ נגדיר אלומה ${\mathcal {F}}_{M}$ על ידי ${\mathcal {F}}(U):=M\otimes _{O(X)}O(U)$. אלומות שמתקבלות באופן זה נקראות קוואזי-קוהרנטיות.

אם $M$ נוצר סופית אז האלומה תקרא קוהרנטית. קטגוריית האלומות הקוואזי-קוהרנטיות על יריעה אפינית שקולה לקטגוריית המודולים מעל חוג הפוניקציות הגלובליות על היריעה. באופן דומה קטגוריית האלומות הקוהרנטיות על יריעה אפינית שקולה לקטגוריית המודולים נוצרים סופית מעל חוג הפונקציות הגלובליות על היריעה.

ממשפט סר נובע שתכונת ה (קוואזי-)קוהרנטיות היא מקומית. זאת אומרת שאם $X=\bigcup U_{i}$ הוא כיסוי פתוח אפיני של יריעה אפינית אז אלומה ${\mathcal {F}}$ על $X$ היא (קוואזי-)קוהרנטית אם ${\mathcal {F}}_{U_{i}}$ היא (קוואזי-)קוהרנטית. עבור יריעה לא אפינית, אלומה (קוואזי-)קוהרנטית מוגדרת להיות אלומה שהיא (קוואזי-)קוהרנטית באופן מקומי.

במקור השתמשו באלומות קוהרנטיות כדי לחקור אפסים וקטבים של פונקציות רציונליות. מחקר זה הוביל למשפט רימן-רוך, מחקר ההומולוגיה של אלומות קוהרנטיות ודואליות סר.

קשר לאגדים

אלומות קוהרנטיות משמשות גם למחקר של משפחות מרחבים ליניאריים בעלות פרמטר שנע ביריעה אלגברית. בהינתן אלומה קוהרנטית ${\mathcal {F}}$ על יריעה אלגברית $X$ ניתן להגדיר את הסיב ${\mathcal {F}}|_{x}$ של ${\mathcal {F}}$ בנקודה $x\in X$ על ידי

${\mathcal {F}}|_{x}:={\mathcal {F}}(U)/{\mathfrak {m}}_{x}{\mathcal {F}}(U)$,

כאשר $U\subset X$ היא סביבה פתוחה אפינית של $x$, ו ${\mathfrak {m}}_{x}\subset O_{X}(U)$ הוא האידיאל המקסימלי שמתאים לנקודה $x\in U$.

אם האלומה ${\mathcal {F}}$ היא חופשית מקומית, זאת אומרת שקיים כיסוי אפיני פתוח $X=\bigcup U_{i}$ כך ש ${\mathcal {F}}(U_{i})$ הוא מודול חופשי מעל $O_{X}(U_{i})$, אז על מערכת המרחבים $\{{\mathcal {F}}|_{x}|x\in X\}$ יש מבנה טבעי של אגד. זאת אומרת שקיים אגד $E_{\mathcal {F}}$ כך שהסיבים שלו איוזומורפיים קנונית לסיבי האלומה ${\mathcal {F}}$. יתר על כן ההתאמה ${\mathcal {F}}\mapsto E_{\mathcal {F}}$ מגדירה שקילות קטגורית בין קטגוריית האלומות החופשיות על $X$ מקומית וקטגוריית האגדים על $X$.

לאור האמור למעלה, לעיתים מגדירים אגד וקטורי על יריעה אלגברית בתור אלומה קוהרנטית חופשית מקומית. כמו כן ניתן לחשוב על אלומות קוהרנטיות בתור הכללת המושג אגד. הכללה זאת מאפשרת להגדיר גרסאות של האגדים הסטנדרטיים מטופולוגיה דיפרנציאלית גם עבור יריעות לא חלקות. לדוגמה, אף על פי שעל יריעה אלגברית לא חלקה לא ניתן להגדיר את האגד הקו-משיק (זאת אומרת אגד שסיביו הם המרחבים הקו משיקים), ניתן להגדיר את האלומה הקו-משיקה (אלומה שסיביה הם המרחבים הקו משיקים).

קטגורית האלומות הקוהרנטיות

קטגורית האלומות ה (קוואזי-)קוהרנטיות היא קטגוריה אבלית. שתי הקטגוריות כמו גם הקטגוריות הנגזרות שלהן הן אינווריאנטים חשובים של יריעה אלגברית. חקר היחסים בין קטגורית אלה עבור יריעות שונות מתואר בספר Residues and duality. חקר זה מכיל בין היתר את דואליות גרותנדיק שהיא הכללה של דואליות סר.

סוגי אלומות נוספים

אלומות קונסטרקטביליות

ערכים מורחבים – אלומה קונסטרקטבילית

טופולוגית זריצקי היא טופולוגיה חלשה מאוד. היא אומנם מספיקה למחקר בסיסי של יריעות אלגבריות אך איננה משקפת את המבנה של היריעה מנקודת מבט של טופולוגיה אלגברית. לכן קשה לחקור את הגאומטריה של היריעה על ידי אלומות בטופולוגית זריצקי. אם יריעה $X$ מוגדרת מעל שדה המרוכבים אז על $X(\mathbb {C} )$ יש טופולוגיה המושרית מהטופולוגיה של $\mathbb {C}$. קטגוריית האלומות בטופולגיה זאת משקפת את המבנה הגאומטרי של היריעה טוב יותר. חשיבות מיוחדת ניתנת לאלומות קבועות מקומית בטופולוגיה זאת. קטגוריית האלומות הקבועות מקומית אינה נשמרת תחת פעולות בסיסיות עם אלומות (כגון דחיפה ומשיכה). אלומות קונסטרקטביליות (ניתנות לבנייה) מוגדרות בתור כל האלומות שמתקבלות מדחיפה ומשיכה של אלומות קבועות מקומית, תחת העתקות אלגבריות.

אלומות אטל

ערכים מורחבים – אלומת אטל, טופולוגית אטל

הטופולוגיה הנ"ל על $X(\mathbb {C} )$ איננה מוגדרת במונחים של גאומטריה אלגברית, ובפרט אינה ניתנת להכללה לשדות סגורים אלגברית כלליים. בשנות החמישים והשישים גרותנדיק פיתח מספר אנלוגים לטופולוגיה זאת המוגדרים במונחים של גאומטריה אלגברית ותקפים מעל שדה כלשהו. האנלוג הנפוץ ביותר הוא טופולוגיית אטל. טופולוגיית אטל איננה טופולוגיה במובן הרגיל של המילה, אלא במובן כללי יותר שנקרא טופולוגיית גרותנדיק. המושג טופולוגיית גרותנדיק תוכנן כך שיהיה אפשר להגדיר את המושג אלומה על מרחב המצויד בטופולוגיית גרותנדיק. אלומות על יריעה אלגברית ביחס לטופולוגיית אטל נקראות אלומות אטל. טופולגיית אטל לא מהווה תחליף מושלם לטופולוגיה על $X(\mathbb {C} )$. בעוד שאלומות של קבוצות (וחבורות) סופיות בטופולוגיית אטל דומות מאוד לאלומות עלֹ $X(\mathbb {C} )$ (למשל קטגורית האלומות הקבועות מקומית של קבוצות סופיות בטופולוגעיית אטל על $X$, שקולה קטגורית האלומות הקבועות מקומית בעלות גבעולים סופיים על $X(\mathbb {C} )$) אלומות של קבוצות (וחבורות) אין-סופיות בטופולוגיית אטל לא דומות כלל לאלומות עלֹ $X(\mathbb {C} )$ ועניות הרבה יותר.

באנלוגיה עם המקרה המרוכב, ניתן להגדיר עבור כל שדה $F$ וכל יריעה $X$ המוגדרת מעל $F$ את המושג אלומות אטל קונסטרוקטביליות מעל $X$. בפרט, עבור חוג סופי $A$ נתן להגדיר את המושג אלומות אטל קונסטרוקטביליות של $A$-מודולים מעל $X$. מקרה פרטי חשוב הוא כאשר החוג הסופי הוא $\mathbb {Z} /l^{n}\mathbb {Z}$ עבור מספר ראשוני $l$ הזר למציין השדה $F$. בדרך כלל הביטוי אלומות אטל מתייחס למקרה זה.

אלומת $l$-אדיות

ערכים מורחבים – אלומה $l$-אדית, אלומות וייל

כאמור, אם $A$ אינו חוג סופי, אז אלומות אטל של $A$-מודולים אינן משקפות את הגאומטריה של $X$. לכן לא ניתן להגדיר אלומות אטל של $\mathbb {C}$-מודולים. תחת זאת משתמשים בבנייה הבאה: משאיפים את $n$ לאינסוף ומקבלים קטגוריה שנקראת "קטגוריית האלומות הקונסטרוקטביליות של $\mathbb {Z} _{l}$-מודולים" או בקצרה "קטגוריית האלמות ה-$l$-אדיות". למרות שמה, האובייקטים בקטגוריה זאת אינם אלומות כלל. בפרט הן אינן אלומות של $\mathbb {Z} _{l}$-מודולים בטופולוגיית אטל. מקטגוריה זאת ניתן לבנות קטגוריוה הנקראת "קטגוריית האלומות הקונסטרוקטביליות של $\mathbb {Q} _{l}$-מודולים". באופן דומה עבור כל הרכבה $F$ של $\mathbb {Q} _{l}$ ניתן להגדיר אלמות הקונסטרוקטביליות של $O_{F}$-מודולים ו-$F$-מודולים. על ידי מעבר לגבול, מקבלים את הקטגוריות של האלומות הקונסטרוקטביליות של ${\bar {\mathbb {Q} }}_{l}$-מודולים ו-$O_{{\bar {\mathbb {Q} }}_{l}}$-מודולים. כל סוגי האלומות האלה נקראות לעיתים "אלמות $l$-אדיות".

מכיוון ש-${\bar {\mathbb {Q} }}_{l}$ איזומורפי ל-$\mathbb {C}$ אפשר להגדיר כך (באופן לא קנוני) אלומות מרוכבות ליריעה אלגברית מעל שדה כלשהו. מכאן אפשר להגדיר הומולוגיות עם מקדמים ב-$\mathbb {C}$ ומספרי בטי ליריעה אלגברית מעל שדה כלשהו. בנייה זאת מראה בפרט שאם $X$ היא יריעה אלגברית מרוכבת ו-$X'$ היא יריעה המתקבלת מ-$X$ על ידי הפעלת אוטומורפיזם על שדה המרוכבים אז מספרי בטי של $X(\mathbb {C} )$ ו$X'(\mathbb {C} )$ שווים. טענה זאת עלולה להפתיע מכיוון שהחבורות היסודית של $X(\mathbb {C} )$ ו-$X'(\mathbb {C} )$ שונות במקרים מסוימים. כאשר $k$ הוא שדה סופי, פייר דלין הגדיר גרסה מעט שונה לאלומה $l$-אדית הנקראת אלומת וייל. אלומות $l$-אדיות ואלומות וייל משחקות תפקיד מרכזי בהוכחה של השערות וייל.

D-מודולים

ערכים מורחבים – D-מודולים

משתמשים באלומת גם כדי לחקור מערכות משוואות דיפרנציאליות על יריעות אלגבריות.

כמו שבשביל לחקור משוואות פולינומיות בתורת גלואה משתמשים בסדרות, וכדי לחקור מערכות משוואות פולינומיות משתמשים באלגבראות, כך גם כדי לחקור מערכות משוואות דיפרנציאליות חלקיות ליניאריות משתמשים במודולים מעלֹ חוג האופרטורים הדיפרנציאליים ב-$n$ משתנים. אם רוצים לחקור משוואות דיפרנציאליות חלקיות על יריעה אלגברית אפינית חלקה אז יש להחליף את חוג האופרטורים הדיפרנציאליים ב-$n$ משתנים בחוג האופרטורים הדיפרנציאליים על היריעה. אם היריעה אינה אפינית אז ייתכן שחוג האופרטורים הדיפרנציאליים יהיה קטן מדי (כמו שחוג הפונקציות הרגולרית על יריעה לא אפינית קטן מדי). לכן יש לחקור אלומות מודולים מעל אלומת החוגים של האופרטורים הדיפרנציאליים. גם לאלומות אלו אפשר להגדיר את תכונת הקוהרנטיות והקוואזי-קוהרנטיות. אלומות קוהרנטיות (ולעיתים גם קוואזי-קוהרנטיות) של מודולים מעל אלומת החוגים של האופרטורים הדיפרנציאליים נקראות D-מודולים. ניתן גם להגדיר את קטגוריית ה-$D$-מודולים ליריעות לא חלקות, אם כי בצורה שונה.

כאמור אפשר לחשוב על $D$-מודול $M$ על יריעה $X$ כעל מערכת משוואות דיפרנציאליות. אם $k=\mathbb {C}$ אז אפשר להגדיר מתי פונקציה אנליטית על $X(\mathbb {C} )$ היא פתרון של $M$. אוסף הפתרונות של $M$ מהווה אלומה קונסטרוקטבילית עלֹ $X(\mathbb {C} )$. בנייה זאת מגדירה פונקטור מקטגורית ה-$D$-מודולים על $X$ לקטגורית האלומות על $X(\mathbb {C} )$. פונקטור זה משרה שקילות מתת קטגוריה של הקטגוריה הנגזרת של $D$-מודולים לקטגוריה הנגזרת של אלומות קונסטרוקטביליות. שקילות זאת שנקראת שקילות רימן-הילברט הוכחה על ידי מאסאקי קשיברו בהתבסס על עבודתו של פייר דלין.

אלומות סוטות

ערכים מורחבים – אלומות סוטות

בהתבסס על עבודה של מרק גורצקי ורוברט מקפרסון תיארו יוסף ברנשטיין, אלכסנדר בילינסון ופייר דלין את התת-קטגוריה של הקטגוריה הנגזרת של אלומות קונסטרוקטביליות המתאימה ל-$D$-מודולים תחת שקילות רימן-הילברט. קטגוריה זאת של אלומות נקראת קטגורית האלומות הסוטות. האובייקטים בקטגוריה זאת אינן אלומות אלא קומפלקסים מסוימים של אלומות. ברנשטין, בילינסון ודלין הגדירו גם אנלוגים של קטגוריה זאת עבור אלומות $l$-אדיות ואלומות וייל. לא ניתן לתאר אנלוגים אלו בעזרת $D$-מודולים מכיוון ששקילות רימן הילברט לא תקפה כאשר $k\neq \mathbb {C}$.

לעיתים קרובות, אלומות סוטות מתנהגות טוב יותר תחת ששת הפנקטורים של גרותנדיק (הפעולות הסטנדרטיות עם אלומות: דחיפה, משיכה וכדומה) מאשר אלומות קונסטרוקטביליות (למשל במשפט הפירוק (Decomposition theorem)). כמו כן לקטגורית האלומות הסוטת יש תכונות טובות יותר בתור קטגוריה אבלית מאשר לקטגורית האלומות קונסטרוקטביליות. למשל כל אלומה סוטה היא מאורך סופי. יתרון מובהק נוסף של האלומות הסוטות היא בנייה הנקראת הרחבה סוטה. בנייה זאת מבוססת על העובדה שלכל אלומה סוטה בלתי-פריקה על תת-יריעה $Y\subset X$ קיימת ויחידה אלומה סוטה בלתי-פריקה המרחיבה אותה על ${\bar {Y}}$. בנייה זאת משמשת לבניית אלומות סוטות מעיניניות רבות, למשל אלומות קרקטרים של לוסטיג.

הגדרות אלטרנטיביות

בספרות קיימות מספר דרכים נוספות להגדיר יריעה אלגברית.

אטלסים ומפות

ניתן להגדיר יריעה אלגברית בצורה דומה לזו המקובלת בטופולוגיה דיפרנציאלית עבור יריעות חלקות. גם בצורה זאת יריעה תהיה מרחב טופולוגי עם מבנה נוסף, רק שמבנה זה יהיה אטלס במקום אלומת פונקציות. כל מפה באטלס תתאים לקבוצה פתוחה אפינית. דרך זאת מעלה מספר קשיים מכיוון שחיתוך של שתי קבוצות אפיניות איננה בהכרח אפיניות, פונקציות המעבר הן בין קבוצות לא אפיניות. לכן יש צורך להגדיר מורפיזמים של קבוצות קוואזי-אפיניות לפני שמגדירים יריעה כללית. מסיבה זאת ומסיבות היסטוריות דרך הגדרה זאת איננה פופולרית.

כמקרה פרטי של סכמות

מנקודת מבט מודרנית ניתן לראות ביריעות אלגבריות מקרה פרטי של סכמות. נקודת מבט זאת מולידה הגדרה אלטרנטיבית של יריעות אלגבריות: יריעה אלגברית היא סכמה המקיימת תכונות מסוימות (מצומצמת ומטיפוס סופי מעל $k$). מצב זה עלול ליצור בלבול, מכיוון שההגדרה המקובלת של סכמה גם כן מבוססת על מושג המרחב הטופולוגי: סכמה היא מרחב טופולוגי עם מבנה נוסף. אולם המרחב הטופולוגי המתאים ליריעה $X$ שונה מהמרחב הטופולוגי המתאים ל-$X$ כאשר חושבים עליה כעל סכמה. לדוגמה אם $X$ איננה מממד $0$ אז המרחב הטופולוגי המתאים אליה כסכמה אינו מקיים את אקסיומת ההפרדה $T_{1}$.

בלבול זה גורם בתורו לבלבול בהגדרת מושג הספקטרום. עבור כל k-אלגברה קומוטטיבית עם יחידה נוצרת סופית וללא נילפוטנטים $A$ קיימת ויחידה (עד כדי איזומורפיזם קנוני) יריעה אלגברית אפינית כך ש: $A\cong k[X]$. יריעה זאת נקראת $spec(A)$. כאמור המרחב הטופולוגי המתאים ליריעה זאת תלוי בשאלה האם אנו חושבים עליה כעל יריעה או סכמה. לכן כדי למנוע בלבול זה, אם רוצים לחשוב עליה כעל יריעה מסמנים את המרחב הטופולוגי המתאים ב $specm(A)$ ואם רוצים לחשוב עליה כעל סכמה מסמנים $specp(A)$. האות $m$ באה מהעוֹבדה שיש התאמה בין הנקודות של $specm(A)$ לאידיאלים מקסימליים ב-$A$ והאות $p$ באה מהעוֹבדה שיש התאמה בין הנקודות של $specp(A)$ לאידיאלים ראשוניים ב-$A$. בדרך כלל הסימון $spec$ מסמן את $specp$.

כפונקטורים מיוצגים

עבור יריעה אלגברית $X$ מעל $k$, ו-$k$-אלגברה קמוטטיבית עם יחידה נוצרת סופית וללא נילפוטנטים $A$, ניתן להגדיר את קבוצת הנקודות של $X$ מעל $A$ על ידי $X(A):=Mor(spec(A),X)$, כאשר $Mor$ מסמן את קבוצת המורפיזמים בין שתי יריעות. כאשר $X$ יריעה אפינית אז $X(A)$ היא קבוצת הפתרונות של מערכת המשוואות המגדירה את $X$ כאשר המשתנים רצים ב-$A^{n}$ במקום ב-$k^{n}$. הפונקטור $A\mapsto X(A)$ נקרא פונקטור הנקודות של $X$. ניתן לשחזר את היריעה $X$ מפונקטור הנקודות שלה. טענה זאת היא מעין גרסה חזקה של הלמה של יונדה (Nobuo Yoneda). לכן נתן להגדיר יריעה אלגברית בתור פונקטור מקטגורית ה-$k$-אלגבראות קמוטטיביות עם יחידה הנוצרות סופית וללא נילפוטנטים לקבוצות המקיימים תנאים מסוימים.

גישה זאת אבסטרקטית למדי ולכן אינה פופולרית עבור יריעות אלגבריות, אך היא משמשת לעיתים כדי להגדיר סכמות, והיא הגישה המקובלת כדי להגדיר הכללות של מושג הסכמה כמו מרחב אלגברי וסטקים אלגבריים.

הכללות

עבור שדות לא סגורים אלגברית

ניתן להגדיר יריעה אלגברית מעל שדה $k$ גם כאשר $k$ אינו סגור אלגברית.

עבור שדות מושלמים

באופן כללי, כאשר $k$ שדה מושלם אחת הדרכים לחשוב על אובייקטים מעל $k$ היא בתור אובייקטים מעלֹ הסגור האלגברי ${\bar {k}}$ ביחד עם פעולה של חבורת גלואה $Gal({\bar {k}}/k)$ שאינה שומרת בדיוק על המבנה של האובייקט מעל ${\bar {k}}$ אך משנה אותו בצורה המושרת מהפעולה של $Gal({\bar {k}}/k)$ על ${\bar {k}}$.

באופן מפורש כאשר $k$ שדה מושלם ניתן להגדיר יריעה אלגברית מעל $k$ בתור יריעה $X$ מעל ${\bar {k}}$ יחד עם פעולה $\rho$ של $Gal({\bar {k}}/k)$ על $X({\bar {k}})$ כך שעבור כל $\gamma \in Gal({\bar {k}}/k)$ ההעתקה $\rho (\gamma ):X({\bar {k}})\to X({\bar {k}})$ מקיימת:

1. $\rho (\gamma )$ רציפה על פי טופולוגית זריצקי.
2. לכל קבוצה פתוחה $U\subset X({\bar {k}})$ ולכול פונקציה רגולרית $f\in {\bar {k}}[U]$ הפונקציה המוגדרת על ידי $g(x)=\gamma ^{-1}(f(\rho (\gamma )(x)))$ היא פונקציה רגולרית על $\rho (\gamma )^{-1}(U)$.

עבור שדות כלליים

כאשר $k$ אינו מושלם הגדרה זאת איננה מספקת. לדוגמה אם $k$ סגור ספרבילית אז $Gal({\bar {k}}/k)$ טריוויאלית, אך אין זה הגיוני להגדיר יריעה אלגברית מעל $k$ כמושג המתלכד עם יריעה אלגברית מעל ${\bar {k}}$. יש מספר דרכים להגדיר יריעה אלגברית גם במקרה זה. אולם בדרך כלל נהוג לטפל במקרה זה כמקרה פרטי של סכמות.

סכמות

ערך מורחב – סכמה

אף על פי שמושג היריעה האלגברית כללי למדי, יש למושג זה מספר מגבלות:

1. נדרש לקבוע את השדה $k$, לכן לא ניתן לטפל בו זמנית ביריעות מעל שדות שונים. מגבלה זאת מקשה על שימושים בתורת המספרים כאשר רוצים לקשר בין פתרונות של מערכת משוואות מעל שדה סופי ובין הגאומטריה של היריעה המוגדרת על ידי מערכת זאת מעל $\mathbb {C}$. כמו כן הגדלת השדה מאפשרת הוספה של מספרים טרנסצנדנטים מה שמאפשר יצירה של נקודות גנריות, זאת אומרת נקודות שימצאו בכל קבוצה פתוחה זריצקי המוגדרת מעל השדה המקורי.
2. יריעות לא מאפשרות טיפול בפתרונות של מערכות משוואות מעל חוגים שאינם שדות. גם מגבלה זאת מקשה על שימושים בתורת המספרים שאחת הבעיות המרכזיות בה היא ניתוח של משוואות דיופנטיות.
3. יריעות לא מאפשרות טיפול בשורשים מרובים. לדוגמה היריעה המוגדרת על ידי המשוואה $x^{2}=0$ זהה ליריעה המוגדרת על ידי המשוואה $x=0$. אולם כאשר מנתחים שורשים של פולינום נהוג לקחת בחשבון את ריבוי השורשים ולכן להתייחס לקבוצת השורשים של $x^{2}$ באופן שונה מאשר לקבוצת השורשים של $x$. התייחסות לריבוי השורשים משפרת את הניסוח והשימושיות של מספר משפטים. למשל את המשפט היסודי של האלגברה.

כדי להתמודד עם מגבלות אלה פיתח גרותנדיק את מושג הסכמה. כדי להבין את ההבדל בין סכמות ויריעות אפשר להסתכל תחילה על המקרה האפיני. סכמות אפיניות, כמו יריעות אפיניות מוגדרות על ידי חוג הפונקציות עליהם, אלא שבמקרה של סכמה מסירם את רוב ההגבלות מחוג זה. ראשית לא דורשים שהוא יהיה נוצר סופית מעל שדה, זה מאפשר להתמודד עם מגבלות 1,2 למעלה. שנית מאפשרים לו להכיל נילפוטנטים, זה מאפשר להתמודד עם מגבלה 3. הסרת מגבלת הנילפוטנטים גורמת לכך שהחוג כבר לא חוג פונקציות. לכן כאשר מגדירים סכמה כללית לא מגדירים אותה בתור מרחב טופולוגי עם אלומת פונקציות אלה בתור מרחב טופולוגי עם אלומה של אלגבראות אבסטרקטיות. מבנה כזה נקרא מרחב מחויג.

לויתור על הנוצרות סופית של חוג הפונקצוית הרגולריות ישנן השלכות. כאשר מתאימים לאלגברה יריעה אפינית, משתמשים בספקטרום המקסימלי שלה, זאת אומרת אוסף האידיאלים המקסימליים שלה, בעוד שכשמתאימים לחוג סכמה אפינית, משתמשים בספקטרום הראשוני שלו, זאת אומרת אוסף האידיאלים הראשוניים שלו. הצורך להשתמש בספקטרום ראשוני נובע מכך שבהינתן העתקה בין חוגים כלליים (לאו דווקא נוצרים סופית מעל שדה) אין זה נכון שתמונה הפוכה של אידיאל מקסימלי היא אידיאל מקסימלי, אבל נכון שתמונה הפוכה של אידיאל ראשוני היא אידיאל ראשוני.

הבדל נסף בין סכמות ליריעות הוא הוויתור על הדרישה שהכיסוי של סכמה על ידי סכמות אפיניות היה סופי. דורשים רק קיום של כיסוי פתוח על ידי סכמות אפיניות. ויתור זה אינו פועל יוצא של אחת המגבלות שתוארו מעלה, אלה בא לאור העבדה שסכמות הן מושג מאוד כללי ולכן מוותרים על כל ההגבלות שאינן הכרחיות. סכמות בעלות כיסוי סופי כזה נקראות סכמות קוואזי-קומפקטיות. במקרים רבים כשחוקרים סכמות מצמצמים את הדיון לסכמות קוואזי-קומפקטיות, מכיוון שמשפטים רבים אינם תקפים לסכמות שאינן קוואזי-קומפקטיות.

הכללות נוספות

ערכים מורחבים – מרחב אלגברי, סטק אלגברי, אינסוף סטק, גאמטריה אלגברית ניגזרת

גם למושג הסכמה יש מגבלות, לדוגמה, אין מושג של סכמת מנה של סכמה על פי יחס שקילות. אפילו כאשר היחס שקילות בעל תיאור מגאומטריה אלגברית, ואפשר לצפות משיקולים גאומטריים שמנה כזאת צריכה להיות, למשל כאשר מדובר במנה של סכמה על פי פעולה חופשית של חבורה סופית (שפועלת על ידי העתקות אלגבריות). כדי להתמודד עם מגבלה זאת פותח המושג מרחב אלגברי.

גם הכללה זאת איננה המילה האחרונה. המושג סטק אלגברי מהווה הכללה שלו. הכללה זאת לא נועדה כדי להרחיב את האובייקטים הגאומטריים שעליהם אפשר לדבר, אלה כדי להוסיף מידע נוסף (שאינו לחלוטין גאומטרי) ליריעה. באופן אינטואיטיבי, סטק אלגברי הוא גרופואיד אשר על אוסף האובייקטים שלו יש מבנה של יריעה אלגברית (או באופן כללי יותר מרחב אלגברי). בשונה מיריעות, סכמות ומרחבים אלגבריים, אוסף הסטקים האלגבריים אינו מהווה סתם קטגוריה, אלא 2-קטגוריה. מקרה פרטי חשוב של סטק אלגברי שמכליל את המושג מרחב אלגברי הוא סטק דלין-ממפורד.

מתחילת המאה ה-21 כאשר מושג ה-$\infty$-קטגוריה תפס תאוצה בזכות עבודותיהם של יעקב לוריא (Jacob Lurie) ואחרים, הכלל מושג הסטק האלגברי למושג ה-$n$-סטק ו-$\infty$-סטק. לעיתים מכנים $n$-סטק בשם $(n+1)$-סכמה, כך שאפשר לקרוא ל-$\infty$-סטק גם $\infty$-סכמות. אוסף ה-$\infty$-סטקים אינו מהווה סתם קטגוריה, אלא $\infty$-קטגוריה.

מושג ה-$\infty$-קטגוריה הוליד גם הכללה של $\infty$-סטקים והיא $\infty$-סטקים נגזרים. הטבלה הבאה נועדה להסביר את האופי של הכללה הזאת:

מהות האובייקט $X$	מהות האובייקט $X(R)$ כאשר $R$ הוא חוג קומוטטיבי עם יחידה	מהות אוסף הפונקציות על $X$.
יריעה אלגברית	קבוצה	אלגברה חסרת נילפוטנטים אלגברה נוצרת סופית מעל שדה
סכמה	קבוצה	חוג קמוטטבי עם יחידה
מרחב אלגברי	קבוצה	חוג קמוטטבי עם יחידה
סטק דלין-ממפורד	גרופואיד בעל חבורת אוטומורפיזמים סופיות	חוג קמוטטבי עם יחידה
סטק אלגברי	גרופואיד	חוג קמוטטבי עם יחידה
$\infty$-סטק	$\infty$-גרופואיד. במילים אחרות טיפוס הומוטופי	חוג קמוטטבי עם יחידה
$\infty$-סטק נגזר	$\infty$-גרופואיד	חוג ניגזר קמוטטבי עם יחידה, זאת אומרת $\infty$-גרופואיד בעל מבנה של חוג קמוטטבי עם יחידה.

מושגים מקבילים

הגאומטריה המודרנית חוקרת מספר מחלקות של אובייקטים גאומטריים. יריעות אלגבריות מהוות אחת ממחלקות אלו, לצידם חוקרים גם יריעות טופולוגיות, יריעות חלקות (differentiable manifolds), יריעות אנליטיות, מרוכבות וממשיות, סוגים שונים של יריעות אלגבריות למחצה (למשל יריעות נאש), יריעות אנליטיות p-אדיות, מרחבים אנליטיים קשיחים, מרחבי ברקוביץ', מרחבים פרפקטואידים ועוד. שלוש המחלקות האחרונות הן גרסאות מודרניות ומעודנות יותר של יריעות אנליטיות p-אדיות. יריעות אלה בתורן הן גרסה לא ארכימדית של יריעות אנליטיות מרוכבות וממשיות. יריעות נאש הן יריעות ממשיות חלקות אלגבריות למחצה, הן דומות מאוד ליריעות אלגבריות ממשיות חלקות. אם נקבע $k=\mathbb {R}$, נראה שטבעי להשוות בין יריעות אלגבריות, יריעות אנליטיות ויריעות חלקות. בהשוואה זאת, יריעות אלגבריות הן המחלקה הקשיחה ביותר, ויריעות חלקות הן המחלקה הגמישה ביותר. כל פונקציה אלגברית היא אנליטית וכל פונקציה אנליטית היא חלקה.

על ציר זה (גמישות/קשיחות) יריעות אנליטיות קרובת בהרבה ליריעות אלגבריות מאשר ליריעות חלקות. אחת הסיבות לכך היא שביריעות חלקות יש את משפט פיצול היחידה בעוד שביריעות אלגבריות ואנליטיות הוא לא יכול להתקיים מכיוון שהוא סותר את משפט היחידות (שלא מתקיים עבור פונקציות חלקות; אך מתקיים עבור פונקציות אלגבריות ואנליטיות). למעשה משפט ג.א.ג.א. של סר מתאר שקילות קטגורית בין יריעות אלגבריות פרויקטיביות מרוכבות ובין יריעות אנליטיות פרויקטיביות מרוכבות.

קשיחות זאת גורמת לכך שבמיקרים רבים על יריעה חלקה אחת יש רצף של מבנים של יריעה אלגברית או אנליטית.

הבדל מובהק בין יריעות אלגבריות ואנליטיות הוא העובדה שמשפט הפונקציה ההפוכה לא תקף במקרה האלגברי. הבדל זה הוא המוטיבציה המרכזית להגדרת טופולוגית אטל על יריעות אלגבריות. טופולוגיה זאת מאפשרת במקרים רבים להחליף את משפט הפונקציה ההפוכה ובכך לצמצם את הפער בין יריעה אלגברית ואנליטית. הבדל נוסף בין יריעות אלגבריות לאנליטיות נובע מכך שבעולם האנליטי (כמו גם בעולם החלק) לכל מד"ר יש פתרון ולרוב המד"רים אין פיתרונות אלגבריים.

ברמה הפרקטית מה שמיחד יריעות אלגבריות משאר האובייקטים בגאומטריוה זה האלגבריות שלהן, זאת אמרת שניתן לתאר כל יריעה אלגברית באמצעות כמות סופית של מידע. דבר זה אינו אפשרי עבור אובייקטים גאומטריים אחרים.

הטבלה הבאה מסכמת את ההבדלים בין העולם האלגברי האנליטי והחלק במקרה הממשי:

	יריעות אלגבריות ממשיות	יריעות אנליטיות ממשיות	יריעות חלקות (דיפרנצאבילות)
משפט הפונקציה ההפוכה	לא תקף. המעבר לטופולגית אטל נועד כדי לפתור בעיה זאת	תקף	תקף
משפט הפונקציה הסתומה	לא תקף. אולם רק מפני שמשפט הפונקציה ההפוכה לא תקף. המעבר לטופולגית אטל פותר בעיה זאת	תקף	תקף
משפט היחידות	תקף	תקף	לא תקף
cutoff function	לא קיימות	לא קיימות	קיימות
משפט פיצול היחידה	לא תקף	לא תקף	תקף
משפט יחידות למד"ר	תקף	תקף	תקף
משפט קיום למד"ר	לא תקף	תקף	תקף
אוסף מחלקות האיזומורפיזם של אובייקטים קומפקטיים	רציף; מקומית ממד סופי	רציף; מקומית ממד סופי	בדיד
אוסף מחלקות האיזומורפיזם של אובייקטים כללים	אינסוף ממדי (גם מקומית) אך לא פיראי לחלוטין	פיראי לחלוטין	פיראי לחלוטין
הכללות עבור שדות אחרים	קיימות לכל שדה וגם מעבר לכך.	קיימות עבור שדות מקומיים, אך שונות למדי ובחלק מהמקרים ללא גרסה מוסכמת אחת	כמעט לא קיימות, לשדות מקומיים יש גרסאות מסוימות אך לא מפותחות ולא פופולריות.
נתנות לתיאור על ידי מידע סופי	כן	לא	לא

דוגמאות

נקודה ויריעות 0-ממדיות אחרות

בהינתן שדה סגור אלגברית $k$, הנקודה היא היריעה האלגברית הקשירה היחידה ממד 0 מעל $k$. היא האובייקט הסופי בקטגוריה של יריעות אלגבריות מעל $k$. כל יריעה אלגברית ממד 0 מעל $k$ היא קו-מכפלה של נקודות. זאת אומרת קבוצה סופית בדידה. לכן מחקר של יריעות אלגבריות ממד 0 לא מהווה עינין. מעל שדה לא סגור המצב מסובך יותר. למשל, אם השדה מושלם אז יריעות 0-ממדיות מעליו ניתנות לתיאור על ידי קבוצות סופיות יחד עם פעולה של חבורת גלואה האבסולוטית של השדה. אובייקט זה מסובך בהרבה, אך אינו גאומטרי כלל והמחקר שלו לא מתבצע במסגרת הגאומטריה האלגברית בדרך כלל. להבדיל, המצב עם סכמות אינו כזה. סכמות ממד 0 מסובכות בהרבה, אומנם הן עדין אובייקט אלגברי ביסודו, אך למחקר שלהן השלכות רבות בגאומטריה אלגברית.

מרחב אפיני ומרחב פרויקטיבי

ערכים מורחבים – מרחב אפיני, מרחב פרויקטיבי

המרחב האפיני הוא הארכי טיפוס של הירעות האפיניות. לשאלות רבות על יריעות אפיניות יש רדוקציה למרחבים אפיניים. לדוגמה, ניתן לשכן את קטגורית האלומות הקוהרנטיות על יריעה אפינית לתוך קטגורית האלמות הקוהרנטיות על המרחב האפיני. למרות פשטותו היחסית, יש מספר השערות קשות הקשורת אליו. המפורסמת בהן היא השערת היעקוביאן.

חבורת האוטומורפיזמים של מרחב אפיני עשירה מאוד. היא אינסוף ממדית ומסובכת. ישנן מספר השערות הקשורות לחבורה זאת.

באופן דומה המרחב הפרויקטיבי הוא הארכי טיפוס של היריעות הפרויקטיביות. לשאלות רבות על יריעות פרויקטיביות יש רדוקציה למרחבים פרויקטיביים. יתר על כן, באמצעות הלמה של צ'ו ניתן גם להכליל תשובות לשאלות אלה ליריעות שלמות.

חבורת האוטומורפיזמים של מרחב פרויקטיבי עשירה למדי אך לא מסובכת. היא החבורה האלגברית הליניארית (מממד סופי) $PGL_{n+1}$.

סדרה של טרנספורציות (אלגבריות, הפיכות) של המישור האפיני, אשר הולכות ונהיות מסובכות יותר. טרמספורמציות אלה אינן אפיניות. טררנספורמציות אפיניות הן טרנספורמציות אלגבריות פשוטות ביותר (שילוב של הזזות וטרנספורמציות ליניאריות)

דוגמאות לטרנספורמציות (אלגבריות, הפיכות) של המישור הפרויקטיבי. טרנספורמציות כאלה נקראות טרנספורמציות פרויקטיביות.

עקומים

ערך מורחב – עקום אלגברי

עקום אלגברי הוא יריעה אלגברית חד-ממדית. בדרך כלל דושים שעקום יהיה בלתי-פריק. אם לא דורשים זאת אז דורשים שכל רכיבי האי-פריקות שלו יהיו חד־ממדיים. עקום שלם הוא תמיד פרויקטיבי. למרות פשטותם היחסית, המחקר של עקומים אלגבריים הוא עשיר ומאתגר. משפטים רבים בגאומטריה אלגברית הוכחו תחילה עבור עקומים ואחר כך הוכללו עבור יריעות כלליות. במקרים רבים הוכחת המשפט לעקומים שונה מאוד מהרדוקציה מיריעה כללית לעקום. בהרבה מקרים ההוכחה לעקומים בתבססת על חישובים מפורשים בעוד שהרדוקציה למקרה של עקום מתבססת על כלים כללים של גאומטריה אלגברית.

עקומים שלמים חלקים

יש מיון ידוע של עקומים חלקים שלמים. האינווריאנט הממיין הראשי של עקומים כאלה הוא הגנוס. במקרה $k=\mathbb {C}$ המרחב $X(\mathbb {C} )$ הוא משטח טופולוגי סגור אורינטבילי, והגנוס של $X$ הוא הגנוס של $X(\mathbb {C} )$ כמשטח טופולוגי. מזה נובע שמחלקת הדיפאומורפיזם של $X(\mathbb {C} )$ תלויה רק בגנוס של $X$ אם $X$ הוא עקום שלם חלק מרוכב. בהינתן גנוס קבוע $g$ יש מבנה של יריעה אלגברית (ליתר דיוק של סטק דלין ממפורד) על אוסף כל מחלקות האיזומורפיזם של עקומים מגנוס $g$.

יש עקום יחיד מגנוס 0. הוא הישר הפרויקטיבי. זה העקום החלק השלם היחיד המהווה יריעת פאנו. עקומים מגנוס 1 נקראים עקומים אליפטיים. יש משפחה חד פרמטרית של עקומים כאלה (הפרמטר נקרא אינווריאנט $j$ של העקום והוא רץ ב-$k$). לעקומים אליפטיים מקום מיוחד בחקר העקומים ובגאומטריה אלגברית בכלל. על כל עקום אליפטי יש מבנה של חבורה אלגברית. חבורת האוטומורפיזם של עקום אליפטי (כשחושבים עליו כיריעה) היא הרחבה סופית של העקום עצמו (כשחושבים עליו כחבורה). עקומים אליפטיים הם העקומים החלקים השלמים היחידים המהווים יריעות קאלאבי-יאו.

עקום אלגברי שלם חלק שהתפרסם בזכות הקשר שלו למשפט פרמה הוא עקום פרמה.

הספירה של רימן: יצוג גאומטרי של הישר הפרויקטיבי המרוכב. הישר הפרויקטיבי הוא העקום האלגברי החלק השלם היחיד מגנוס 0

טורוס - משטח טופולוגי סגור אוריינטבילי מגנוס 1. אם $X$ הוא עקום אליפטי (עקום אלגברי חלק שלם מגנוס 1) אז $X(\mathbb {C} )$ דיפאומורפי לטורוס.

משטח טופולוגי סגור אוריינטבילי מגנוס 2. אם $X$ הוא עקום אלגברי חלק שלם מגנוס 2 אז $X(\mathbb {C} )$ דיפאומורפי למשטח זה.

משטח טופולוגי סגור אוריינטבילי מגנוס 3. אם $X$ הוא עקום אלגברי חלק שלם מגנוס 3 אז $X(\mathbb {C} )$ דיפאומורפי למשטח זה.

החלק האפיני שני עקומים אליפטיים ממשיים משוכנים במישור. כפי שניתן לראות, ירעות הנקודות הממשייות של עקומים אלו אינן דיפיאומורפיות. אולם ירעות הנקודות המרוכבות שלהם דיפאומורפיות

פעולת החיבור על עקום אליפטי המשוכן במישור. סכום של כל 3 נקודות על אותו ישר הוא 0. הנקודה באינסוף היא-0. (נקודה זאת לא מופיעה בציור, מכיוון שהוא מציג רק את החלק אפיני (וגם לא את כולו).

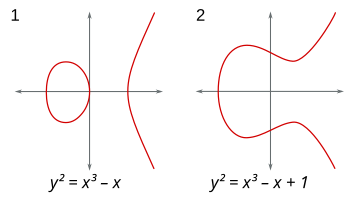
עקומים חלקים

לכל עקום אלגברי חלק יש קומפקטיפיקציה (זאת אומרת עקום שלם המכיל אותו כתת-קבוצה פתוחה צפופה) חלקה יחידה. לכן ניתן למיין עקומים אלגבריים חלקים באמצעות עקומים חלקים שלמים. באופן מפורש יותר, כדי לתאר עקום חלק, צריך לתאר עקום חלק שלם ולהוציא ממנו קבוצה סופית של נקודות.

עקומים סינגולריים

אם העקום אינו חלק אז כל הסינגולריות שלו מבודדות. לכן נהוג לחקור עקומים לא חלקים רק מקומית בסביבת הסינגולריות. אין מיון מלא של כל הסינגולריות האפשריות של עקומים, אבל בהנחות מסוימות על הסינגולריות לעיתים קיים מיון. אחד הדברים שמקלים על המיון הזה היא העובדה שעקום נורמלי הוא תמיד חלק. לכן נורמליזציה של עקום מהווה התרת סינגולריות קנונית שלו.

עקומים מישוריים

עקום מישורי אפיני הוא עקום השוכן במישור האפיני בתור תת-קבוצה סגורה. עקום כזה תמיד ניתן להגדרה על ידי משוואה אחת (משני משתנים). המעלה של המשוואה הזאת נקראת המעלה של העקום. באופן דומה עקום מישורי פרויקטיבי ממעלה $k$ הוא עקום במישור הפרויקטיבי הנתון על ידי משוואה הומוגנית אחת ממעלה $k$ משלושה משתנים. אוסף כל העקומים המישוריים הפרויקטיבים ממעלה $d$ הוא מרחב פרויקטיבי ממד

$${\frac {(d+1)(d+2)}{2}}-1$$

ניתן לחלק מרחב זה לתתי יריעות לפי הטיפוסים השונים של העקומים. מיון של עקומים מישוריים ממעלה נתונה איננה משימה פשוטה. מנקודת מבט מודרנית, מבין כל משימות מיון העקומים המישוריים, קל יותר למיין עקומים מישוריים פוריקטיביים מעל שדה סגור אלגברית (למשל $\mathbb {C}$). ולכן בדרך כלל מתחילים במקרה זה, אחר כך מנסים לעדן את המיון שיתאים לשדות אחרים (למשל $\mathbb {R}$) ולמקרה האפיני. אולם, היסטורית, שדה המרוכבים והגאומטריה הפרויקטיבית התפתחו מאוחר, לכן עקומים ממעלה נמוכה נחקרו תחילה במקרה הממשי האפיני.

עקומים מישוריים ממעלה 1 הם ישרים. אפשר לראות במיון של עקומים מישוריים ריבועיים כנקודת ההתחלה של הגאומטריה האלגברית, הוא היה ידוע עוד ביוון העתיקה. במקרה האפיני הממשי הם:

עקומים מישוריים ריבועיים והקשרים ביניהם

את כל העקומים המישוריים הריבועיים הממשיים האפיניים בעלי הנקודות מלבד "זוג ישרים מקבילים" ניתן לקבל מחיתוך של חרוט על ידי מישור

• פרבולה (איזומורפית לישר)
• היפרבולה (איזומורפית לישר בלי נקודה)
• אליפסה (איזומורפית למעגל)
• שני ישרים מקבילים
• שני ישרים נחתכים
• מעגל עם רדיוס 0 (יריעה בעלת נקודה ממשית 1)
• מעגל עם רדיוס שלילי (יריעה ללא נקודות ממשית כלל)
• זוג ישרים מקבילים מדומים (יריעה ללא נקודות ממשיות כלל)
• ישר אחד (כפול)

המקרה הפרויקטיבי המרוכב פשוט יותר. יש רק שני סוגים של עקומים כאלה: ישר פרויקטיבי וזוג ישרים פרויקטיבים נחתכים.

המיון של עקומים מישוריים ממעלה שלישית מסובך בהרבה, הוא התבצע באופן חלקי על ידי ניוטון ובאופן מלא על ידי פלוקר וכלל למעלה מ-100 מקרים. בשונה ממעלות נמוכות יותר, יש אינסוף מחלקות איזומורפיזם של כאלה עקומים. אולם, במקרה הפריקטיבי המרוכב ניתן לתאר את כל העקומים האלה בקלות יחסית:

עקומים מישוריים ממעלה 3 והקשרים ביניהם

• העקומים חלקים: אלה בדיוק העקומים האליפטיים. יש אינסוף מחלקות איזומורפיזם של עקומים כאלה, אך יריעות הנקודות שלהם הומיומורפיות.
• עקום נודלי: עקום בלתי פריק עם סינגולריות נודלית. סינגולריות נודלית היא סינגולריות הנראית (מקומית בטופולוגית אטל או האנליטית) כמו זוג ישרים נחתכים. הנורמליזציה של עקום זה היא הישר הפרויקטיבי. אפשר לתאר את החלק האפיני של העקום על ידי המשוואה

$$y^{2}=x^{2}\cdot (x+1)$$

למשל. עקומים נודליים (לצד ניוונם - עקומים קספידיים) הם העקומים המישוריים הרציונליים ממעלה 3. זאת אומרת, עקומים שיש להם פרמטריזציה על ידי זוג פולינומים ממעלה 3. מסיבה זאת הם שימושיים בגרפיקה וקטורית. מושג ה-cubic spline מבוסס על עקומים אלה. כאשר מציגים עקום בגרפיקה וקטורית באמצעות cubic spline, מחלקים אותו למקטעים המהווים עקום נודלי. אומנם עקומים נודליים מכילים חיתוכים עצמיים, חיתוכים אלה נמצאים בדרך כלל מחוץ למקטעים, ולכן לא מופיעים ב-spline.

• עקום קספידלי: עקום בלתי פריק עם סינגולריות יחידה בצורת חוד. גם הנורמליזציה של עקום זה היא הישר הפרויקטיבי. אפשר לתאר את החלק האפיני של העקום על ידי המשוואה
  $$y^{2}=x^{3}$$

למשל.

• ישר ועקום (בליתי פריק) ממעלה 2 הנחתכים בשתי נקודות. עקום זה איזומורפי לאיחוד של שני ישרים פרויקטיביים הנחתכים ב-2 נקודות.
• ישר ועקום (בליתי פריק) ממעלה 2 המשיקים בנקודה אחת. עקום זה איזומורפי לאיחוד של שני ישרים פרויקטיביים המשיקים בנקודה אחת.
• שלושה ישרים הנחתכים ב-3 נקודות.
• שלושה ישרים הנחתכים בנקודה אחת.
• שני ישרים נחתכים (אחד מהם כפול)
• ישר אחד (מריבוי 3).

הגנוס של עקום מישורי פרויקטיבי חלק ממעלה $d$ הוא

$$g={\frac {(d-1)(d-2)}{2}}$$

משטחים

ערך מורחב – משטח אלגברי

משטח אלגברי הוא יריעה אלגברית דו-ממדית. משטחים אלגבריים מסובכים בהרבה מעקומים אך עדיין פשוטים יותר מיריעות כלליות. משטחים חלקים שלמים הם תמיד פרויקטיביים אולם משטחים שלמים שאינם חלקים לאו דווקא.

סינגולריות של משטחים

סינגולריות של משטח נורמלי היא תמיד מבודדות, לכן כשחוקרים אותה בדרך כלל מתמקדים בסביבה של נקודה סינגולרית. גם כאן כמו בעקומים אין מיון כללי אולם אם מגבילים את הסינגולריות לפעמים ניתן למין אותן. לדוגמה יש מיון אלגנטי של כל סוגי הסינגולריות של משטחים שהם רציונלים וגורנשטיין. המיון מתאים לסינגולריות אלה דיאגרמות דינקין מטיפוסים A,D,E (דיאגרמות ללא קשתות מרובות; simply laced diagrams). סינגולריות אלה נקראות סינגולריות דה-ואל (וגם סינגולריות קליין, סינגולריות משטחית פשוטה, נקודה רציונלית כפולה). ניתן לקשר בין סינגולריות אלה והתת חבורות הסופיות של $SO(3)$ (או של $SL_{2}$) הממוינות על ידי אותן דיאגרמות. משפט בריסקונד גם מקשר בין סינגולריות אלה ואלגבראות הלי הפשוטות שמתאימות לאותן דיאגרמות.

סינגולריות דו-ואל ודיאגרמות דינקין שלהן

התרת סינגולריות

התרת סינגולריות עבור משטחים פשוטה יותר מאשר עבור יריעות אלגבריות כלליות. היא הוכחה על ידי זריצקי כעשור לפני שהוכחה על ידי הרונקה עבור יריעות אלגבריות כלליות (מעל שדה עם מאפיין 0). כמו כן היא הוכחה גם עבור מאפיין חיובי, בעוד שהתרת סינגולריות במקרה הכללי עודנה פתוחה עבור מאפיין חיובי.

מודל מינימלי

בכל מחלקת שקילות בירציונלית קיים משטח חלק שלם שאינו ניפוח (לאורך מרכז חלק) של אף משטח חלק אחר. משטח זה נקרה מודל מינימלי של המחלקה. ברוב המקרים משטח זה יחיד, ובאלה שהוא אינו יחיד יש תיאור פשוט לכל המודלים המינימליים. עובדה זאת מקלה על מיון המשטחים עד כדי שקילות בירציונלית.

בממדים גדולים יותר המצב מסובך יותר, הניסיונות להבין אותו נקראים "תוכנית המודל מינימלי".

משטחים במרחב

החקר של משטחים במרחב דומה במקצת לחקר עקומים מישוריים (אך מסובך בהרבה). גם כאן ניתן למין אותם לפי מעלתם. משטחים ממעלה 1 הם מישורים. במקרה הפרויקטיבי המרוכב יש רק 3 טיפוסי איזומורפיזם של משטחים ממעלה 2: מישור פרויקטיבי, זוג מישורים פרויקטיבים נחתכים והחרוט הריבועי. במקרה האפיני הממשי, יש את הטיפוסים הבאים:

משטחים ריבועיים והקשרים ביניהם

• פרבולואיד היפרבולי, גליל פרבולי, פרבולואיד אליפטי. כולם איזומורפיים למישור
• זוג מישורים מקבילים
• זוג מישורים נחתכים
• גליל אליפטי
• החרוט הריבועי
• אליפסואיד
• היפרבולואיד חד-יריעתי
• היפרבולואיד דו-יריעתי
• גליל מרדיוס 0 (יריעה שהנקודות הממשיות שלה מהוות ישר)
• אליפסואיד מרדיוס 0 (יריעה שהנקודות בעלת נקודה ממשית 1)
• אליפסואיד מרדיוס שלילי (יריעה ללא נקודות ממשיות כלל)
• גליל מרדיוס שלילי (יריעה ללא נקודות ממשיות כלל)
• זוג מישורים מקבילים מדומים (יריעה ללא נקודות ממשיות כלל)
• מישור אחד (כפול)

משטח קלבש. משטח מרחבי ממשי ממעלה 3 שכל 27 הישרים שעליו הם ממשיים

יש אינסוף טיפוסי איזומורפיזם של משטחים מרחביים ממעלה 3. אולם, יריעות הנקודות של משטחים מרוכבים פרויקטיביים חלקים ממעלה 3 כולן הומיאומורפיות. כמו כן כל אחד ממשטחים אלה מכיל בדיוק 27 ישרים.

אוסף כל המשטחים הפרויקטיביים במרחב ממעלה $d$ הוא מרחב פרויקטיבי מממד

$${\frac {(d+3)(d+2)(d+1)}{6}}-1$$

היפר-משטחים

היפר-משטח הוא יריעה מממד $n-1$ (במקרה שהיריעה פריקה דורשים את אותו התנאי על כל רכיב אי-פריקות) במרחב (פרויקטיבי או אפיני) מממד $n$.

היפר-משטחים הם הכללה ישירה של עקומים מישוריים ומשטחים מרחביים. המחקר של היפר-משטחים קל יותר מאשר של יריעות כלליות. הסיבה המרכזית לכך היא שהם מוגדרים על ידי פולינום בודד. כך שלחקור אותם זה בעצם לחקור את הפולינום הזה. אפשר ללמוד הרבה על ההיפר משטח מפאון ניוטון של הפולינום הזה.

אחת הדוגמאות הפשוטות ביותר להיפר-משטח סינגולרי היא הקונוס הריבועי. במקרה האפיני זאת היריעה המוגדרת על ידי המשוואה

$$\sum _{i=1}^{n}a_{i}x_{i}^{2}=0$$

כאשר $a_{i}$ הם פרמטרים קבועים שאינם מתאפסים. אם $k$ סגור אלגברית אז אין חשיבות לערכם של פרמטרים אלו.

אוסף כל ההיפר-משטחים הפרויקטיביים במרחב מממד $n$ ממעלה $d$ הוא מרחב פרויקטיבי מממד

$$.{\binom {n+d}{d}}-1={\binom {n+d}{n}}-1$$

חבורות אלגבריות ויריעות קשורות

ערך מורחב – חבורה אלגברית

חבורה אלגברית היא יריעה אלגברית שיש עליה מבנה של חבורה, כך שהעתקות הכפל והיפוך הן מורפיזמים של יריעות אלגבריות. לצד היותם מושא מחקר חשוב בתורת החבורות ותורת ההצגות, חבורה אלגברית מהוות מקור חשוב לדוגמאות של יריעות אלגבריות. בדרך כלל המחקר של חבורות אלגבריות מתחלק לשני סוגי חבורות:

• יריעות אבליות - אלו הן חבורות אלגבריות אשר שלמות כיריעות אלגבריות.
• חבורות ליניאריות - אלו הן חבורות אלגבריות אשר אפיניות כיריעות אלגבריות. באופן שקול אלו הן חבורות המהוות תתי-חבורות של החבורה $GL_{n}$.

במובן מסוים כל חבורה אלגברית מתקבלת משילוב של חבורת מסוגים אלו. (פורמלית: לפי משפט שבלה על המבנה של חבורות אלגבריות (Chevalley's structure theorem) כל חבורה אלגברית קשירה היא הרחבה של חבורה ליניארית ויריעה אבלית)

יריעות אבליות

מנקודת מבט של תורת החבורות, יריעות אבליות אינן מציגות עניין רב. הן תמיד קמוטטיביות, ובמקרה $k=\mathbb {C}$ חבורת הנקודות שלהן איזומורפית כחבורת לי לחבורה $SU(2)^{2n}$. לכן עיקר המחקר עליהן הוא במסגרת הגאומטריה האלגברית. יריעות אבליות חד-ממדיות הן עקומים אליפטיים. ליריעות האבליות יש תפקיד חשוב בגאומטריה אלגברית מכיוון שרכיב הקשירות של היחידה בחבורת פיקאר של יריעה אלגברית חלקה שלמה מעל שדה ממאפין 0 היא יריעה אבלית.

חבורות ליניאריות

החבורות הרדוקטיביות מהוות תת-מחלקה חשובה של החבורות הליניאריות. מנקודת מבט של גאומטריה אלגברית חבורות רדוקטיביות הן המעניינות ביותר בין החבורות הליניאריות. לדוגמה אם $char(k)=0$ אז כל חבורה ליניארית קשירה איזומורפית כיריעה אלגברית לחבורה רדוקטיבית כפול מרחב אפיני. יש מיון של חבורות רדוקטיביות הדומה למיון של אלגבראות לי פשוטות למחצה אך קצת יותר מסובך. מיון זה כולל בין היתר את הסדרות הבאות: $GL_{n}$, $PGL_{n}$, $SL_{n}$, $SO_{n}$, $SP_{n}$. מיון זה נותן בנק של דוגמאות של יריעות אלגבריות. מלבד החבורות עצמן. חבורות אלה מהוות בסיס לבנייתן של יריעות נוספות.

מרחבי מנה

אם $H<G$ תת-חבורה סגורה, אז המנה $G/H$ היא יריעה קוואזי-פרויקטיבית. נניח לצורך דיון זה כי $G$ חבורה רדוקטיבית.

יריעות דגלים: אם היריעה $G/H$ היא פרויקטיבית אז היא נקראת יריעת דגלים (חלקית) ו-$H$ נקראת תת-חבורה פרבולית. יש מיון של תתי-חבורות פרבוליות (הן מתאימית לתתי-קבוצות של קבוצת השורשים הפשוטים של אלגברת הלי של $G$) קימת תת-חבורה פרבולית מינימלית יחידה. היא נקראת תת-חבורת בורל (במקרה ש-$k$ סגור אלגברית). יריעת הדגלים המתאימה נקרת יריעת דגלים המלאים. במיקרה של $GL_{n}$ יריעת הדגלים היא אוסף כל הסדרות העולות של תת-מרחבים ב-$k^{n}$ ממדים נתונים. סדרה כזאת נקראת דגל. אם הסדרה היא מקסימלית (ז"א שהממדים הם בדיוק כל המספרים מ1 עד n) אז הדגל נקרא דגל מלא וכך מתקבלת יריעת הדגלים המלאים. דוגמאות נוספות ליריעות דגלים של $GL_{n}$ הן המרחב הפרויקטיבי (יריעת כל תתי המרחבים ממד 1 ב-$k^{n}$) והכללתו - יריעת גרסמן (יריעת כל תתי המרחבים ממד $m$ ב-$k^{n}$).

יריעות סימטריות: אם $H$ היא חבורת נקודות השבט של אוטומורפיזם מסדר 2 של $G$ אז היא נקראת תת-חבורה סימטרית של $G$ והמנה $G/H$ נקראת יריעה סימטרית. יש מיון של יריעות סימטריות (ביחס לחבורות רדוקטיביות) הדומה למיון של חבורות רדוקטיביות אך מסובך ממנו. הדוגמה הקלאסית למרחב סימטרי היא מרחב התבניות הריבועיות הלא מנוונות על מרחב ליניארי, ביחס לפעולת החפיפה של $GL_{n}$. כל חבורה $G$ היא מרחב סימטרי ביחס לחבורה $G\times G$. אפשר לחשוב על יריעות סימטריות כעל הכללה של דוגמה זאת, וכך על חקר של יריעות סימטריות כעל הכללה של תורת החבורות האלגבריות.

יריעות ספריות: יריעה ספרית היא יריעה נורמלית $X$ עליה פועלת חבורה אלגברית (רדוקטיבית) $G$ כך שלתת-חבורת בורל של $G$ יש מספר סופי של מסלולים על $X$. מחקר של מרחבים ספריים בדרך כלל מתמקד במרחבים ספריים טרנזיטיביים. אם $G/H$ הוא מרחב ספרי אז $H$ נקראת תת-חבורה ספרית. כל יריעה סימטרית הוא ספרית. יריעות דגלים גם כן ספריות. יש מיון של יריעות ספריות טרנזיטיביות אפיניות הדומה למיון של יריעות סימטריות אך מסובך ממנו בהרבה.

יריעות שוברט

יריעת שוברט היא סגור של מסלול של תת-חבורה פרבולית $P<G$ על יריעת דגלים של $G$. חקר יריעות שוברט והאינטראקציה ביניהן הוא תחום חשוב בגאומטריה אלגברית. לתחום זה יש שימושים רבים בתורת ההצגות. הקשר בין יריעות שוברט לתורת ההצגות מבוסס על השערות קשדן-לוסטיג שהוכחו על ידי בילינסון-ברנשטיין וברלינסקי-קשיווארה.

יש אנלוג של יריעת שוברט עבור מרחבים ספריים: סגור של מסלול של חבורה פרבולית על מרחב סימטרי.

הקונוס הנילפוטנטי ויריעות קשורות

כל חבורה פועלת על עצמה על ידי הצמדה. אחד מנושאי המחקר בחבורות אלגבריות הוא המסלולים של פעלוה זאת עבור חבורות רדוקטיביות $G$. בזכות פירוק ז'ורדן (ומשפט החתך של לונה) כדי להבין שאלות רבות על מסלולים אלה, די להבין שני מקרים:

• מסלולים פשוטים-למחצה – מסלולים סגורים
• מסלולים אוניפוטנטיים – מסלולים שאיבר היחידה נמצא בסגור שלהם.

המסלולים הפשוטים-למחצה קלים יחסית לניתוח. לכן עיקר העניין הוא במסלולים האוניפוטנטיים.

יש מספר סופי של מסלולים אוניפוטנטיים. איחודם נקרא הקונוס האוניפוטנטי. הוא איזומרפי (כיריעה אלגברית יחד עם הפעולה של $G$) לקונוס הנילפוטנטי המהווה את אוסף כל האיברים הנילפוטנטים באלגברת-הלי ${\mathfrak {g}}$ של החבורה $G$. ז"א איברים ש-0 נמצא בסגור של המסלול שלהם תחת הפעולה הצמודה של $G$ על ${\mathfrak {g}}$. באופן שקול, אלה הם האיברים של האלגברה הנגזרת $[{\mathfrak {g}},{\mathfrak {g}}]$ שפעולתם הצמודה היא נילפוטנטית. הקונוס הנילפוטנטי, כמו גם סגורים של מסלולים נילפוטנטיים מהווים נושא מחקר חשוב בגאומטריה אלגברית ותורת החבורות האלגבריות. ליריעות אלה יש התרת סינגולריות $G$-אקויברינטית טבעית המבוססת על יריעות דגלים. במקרה שהמסלול הנלפוטנטי הוא רגולרי, אנו מקבלים התרה של הקונוס הנילפוטנטי הנקראת התרת שפרינגר. המרחב המתיר בהתרה זאת הוא האגד הקו-משיק ליריעות הדגלים המלאה של $G$. הסיב של נקודה תחת התרה זאת נקרא סיב שפרינגר. מחלקת האיזומורפיזם שלו תלויה רק במסלול של הנקודה (ולכן לכל חבורה יש רק מספר סופי של סיבי שפרינגר). לסיבי שפרינגר חשיבית רבה בגאומטריה אלגברית ותורת ההצגות.

עבור בחבורה האלגברית הפשוטה הקטנה ביותר $SL_{2}$ הקונוס הנילפוטנטי הוא הקונוס הריבועי במרחב.

יש גם קונוס נילפוטנטי במרחב ${\mathfrak {g}}^{*}$ הדואלי ל-${\mathfrak {g}}$. אם $G$ רדוקטיבית, אז ${\mathfrak {g}}\cong {\mathfrak {g}}^{*}$ כהצגות של $G$ (ביחס לפעולה הצמודה). לכן גם הקונוסים הנילפוטנטיים איזומורפיים. אולם לחבורה אלגברית ליניארית כללית זה לא נכון. בהרבה מקרים דווקא הגרסה הדואלית יותר שימושית בתורת ההצגות. למשל בשיטת המסלולום של קוסטנט-קירילוב.

לקונוס הנילפוטנטי יש גם גרסה עבור מרחב ספרי: בהינתן $G$-מרחב ספרי $X$ ונקודה $x\in X$, יש לנו העתקה $G\to X$. הקו-דיפרנציאל של ההעתקה הזאת היא שיכון $T_{x}^{*}(X)\to {\mathfrak {g}}^{*}$. התמונה ההפוכה של הקונוס הנילפוטנטי תחת שיכון זה נקראת הקונוס הנילפוטנטי היחסי של המרחב הספרי $X$.

יריעות הצגות

בהינתן חבורה אלגברית $G$ וחבורה (דיסקרטית) נוצרת סופית $\Gamma$ ניתן להגדיר מבנה טבעי של יריעה אלגברית על אוסף ההומומורפיזמים מ-$\Gamma$ ל-$G$. ליריעה זאת קראים יריעת ההצגות (של $\Gamma$ ב-$G$). החבורה $G$ פעלת על יריעת ההצגות המתאימה. לעיתים מתעניינים במנה על פי פעולה זאת (ובהתאם להקשר גם היא לעיתים מכונה יריעת ההצגות).

מקרה פרטי חשוב מהווה הדוגמה $\Gamma =\mathbb {Z} ^{2}$. במקרה זה יריעת ההצגות מכונה גם היריעה המתחלפת. הכללה מעניינת של דוגמה זאת היא המקרה בו $\Gamma =\pi _{1}(\Sigma )$, כאשר $\Sigma$ הוא משטח רימן קומפקטי. לאור התאמת רימן הילברט יריעת ההצגות הזאת קשורה קשר הדוק למרחב ההשתנות (ראו להלן) של ה-$G$-מערכות מקומיות על $\Sigma$.

יריעות קויבר

בהינתן קויבר (ז.א. גרף מכוון לאו דווקה פשוט) $Q$, הצגה שלו היא התאמה של מרחב ליניארי לכל קודקוד והעתקה ליניארית לכל חץ. ממד של הצגה של קוויבר הוא רשימת הממדים של המרחבים הליניאריים המתאימים לקודקודים. על אוסף ההצגות מממד נתון של קויבר נתון $Q$ (עד כדי איזומורפיזם) יש מבנה טבעי של יריעה אלגברית. ליריעה זאת קוראים יריעת הקויבר של $Q$. ישנן מספר בנייות המבוססת על בנייה זאת הנקראות (בהתאם להקשר) אף הן יריעת קויבר. לדוגמה יריעת הקויבר של לוסטיג ויריעת הקויבר של נקג'ימה.

יריעת ההצגות של חבורת משטח למקרה של $GL_{n}$ קשורה בקשר הדוק ליריעת הקויבר של לוסטיג של קויבר בעל קודקוד יחיד ומספר קשתות המתחילות ונגמרות בו.

יריעות טוריות

ערך מורחב – יריעה טורית

יריעה טורית היא יריעה $G$-ספרית כאשר $G$ היא טורוס אלגברי (זאת אומרת חבורה אלגברית המהווה מכפלה של מספר עותקים של החבורה הכפלית של שדה ההגדרה). במילים אחרות יריעה טורית היא יריעה אלגברית נורמלית המכילה טורוס אלגברי בתור קבוצה פתוחה צפופה, כך שפעולת הטורוס על עצמו מתרחבת לפעולה אלגברית של חבורה על היריעה. יש תיאור של כל הירעות הטוריות. כל יריעה טורית מתוארת על ידי מבנה קומבינטורי בשם מניפה. תכונת רבות של יריעות טוריות (למשל: חלקות, שלמות, פרויקטיביות...) ניתנות לתיאור על ידי תכונות קומבינטוריות של המניפה המתאימה.

יריעות טוריות מהוות בנק של דוגמאות ליריעות אלגבריות. בזכות התיאור הקומבינטורי שלהן ניתן לבדוק בקלות יחסית השערות רבות עליהן ולקבל מכך אינדיקאציות ליריעות אלגבריות כלליות. לדוגמה קל יחסית לבנות דוגמה ליריעה טורית שלמה ולא פרויקטיבית. למרות פשטותה היחסית של דוגמה זאת, היא איננה הדוגמה הראשונה, וקדמו לה דוגמאות מסובכות יותר.

מרחבי השתנות (Moduli spaces)

משפחה מעניינת של דוגמאות של יריעות אלגבריות, מתקבלת מניסיון למיין מבנים מסוימים בגאומטריה אלגברית. לעיתים על אוסף כל המבנים האלה (עד כדי איזומורפיזם) יש מבנה של יריעה אלגברית. יריעה זאת נקראת מרחב השתנות (באנגלית Moduli space). הדוגמה הקלאסית של מרחב השתנות היא יריעת כל העקומים מגנוס נתון. יריעות הקויבר כמו גם יריעות ההצגות של חבורת משטח שתוארו מעלה הן דוגמאות ליריעות השתנות. כיום נהוג לדבר בדרך כלל על סטקים של השתנות במקום יריעות השתנות. הם קיימים ביותר מקרים ונותנים תמונה מדויקת יותר. אם יריעת ההשתנות קימת ניתן לקבלה מהסטק המתאים לאחר תהליך פשוט מסוים.

ראו גם

• גאומטריה אלגברית
  • יריעה קוואזי-פרויקטיבית
    • יריעה אלגברית פרויקטיבית
    • יריעה קוואזי-אפינית
      • יריעה אלגברית אפינית
  • יריעה פרידה
    • יריעה שלמה
  • יריעה טורית
• יריעה אנליטית
• יריעה חלקה

לקריאה נוספת

• Kempf. Algebraic Varieties.
• Griffiths, Phillip; Harris, Joseph (1978). Principles of Algebraic Geometry. John Wiley & Sons. ISBN 0-471-32792-1.
• Hartshorne, Robin (1977). Algebraic Geometry. Springer-Verlag. ISBN 0-387-90244-9.

קישורים חיצוניים

• יריעה אלגברית, באתר MathWorld (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

38709417יריעה אלגברית