פורטל:מתמטיקה/משפטים והשערות מפורסמים/אוסף

עריכהמשפטים והשערות

משפטים והשערות

לעריכת המשפטים וההשערות לחצו על המספר בכותרת ואחר כך "עריכה".

1

המשפט האחרון של פרמה הוא משפט מפורסם בתורת המספרים שאותו ניסח המתמטיקאי פייר דה פרמה באמצע המאה ה-17, והוא נותר כבעיה פתוחה עד שהוכח על ידי אנדרו ויילס בשנת 1995. במשך כ-350 שנים היה לאחת הטענות המפורסמות ביותר בעולם המתמטיקה שלא הוכחו.

המשפט טוען כי:

עבור n טבעי גדול מ-2, לא קיימים מספרים טבעיים x,y,z המקיימים את המשוואה: $\!\,x^{n}+y^{n}=z^{n}$.

לערך המלא

2

המשפט היסודי של האריתמטיקה הוא המשפט הקובע כי כל מספר טבעי יכול להיכתב כמכפלה ייחודית של מספרים ראשוניים, עד כדי שינוי הסדר של הגורמים. בכלל זה מכפלה של גורם אחד (כאשר המספר הוא ראשוני בעצמו), ומכפלה של אפס גורמים (המספר 1).

למשל, את המספר $\!\,1176$ ניתן לכתוב כמכפלה הבאה של מספרים ראשוניים: $\!\,1176=2^{3}\cdot 3\cdot 7^{2}$. אין שום דרך אחרת לכתוב את המספר הזה בתור מכפלה של ראשוניים.

המשפט מראה כי למספרים הראשוניים חשיבות רבה - הם מהווים את "אבני הבניה" הבסיסיות של כל המספרים. למשפט שימושים רבים, החל במציאת המחלק המשותף המקסימלי של מספרים וכלה בהוכחת משפט אי השלמות של גדל.

לערך המלא

3

משפטי האי שלמות של גדל הינם צמד משפטים יסודיים בלוגיקה מתמטית, הענף החוקר את יסודות הלוגיקה בכלים מתמטיים. קורט גדל הראה שבכל מערכת אקסיומות סופית ועשירה מספיק (כזו המכילה את אקסיומות האריתמטיקה החלשה) קיימות טענות אמיתיות שלא ניתן להוכיחן. בכך הראה גדל שהמושגים 'משפט נכון', ו'משפט מוכח', אינם זהים, ושם קץ לניסיונות רבים לבנות מערכת אקסיומתית שבעזרתה ניתן יהיה לבנות בצורה שיטתית את כל המשפטים הנכונים.

לערך המלא

4

אקסיומת המקבילים היא האקסיומה החמישית והאחרונה בספרו של אוקלידס, "יסודות", שבו פיתח את הגאומטריה האוקלידית מעקרונות היסוד שלה. האקסיומה ידועה גם בשם "האקסיומה החמישית של אוקלידס". האקסיומה קובעת כי דרך נקודה מחוץ לישר ניתן להעביר ישר אחד ויחיד שמקביל לישר הנתון.

האקסיומה בולטת בין שאר האקסיומות של הגאומטריה האוקלידית באורכה ובמורכבותה. רמז לכך שאוקלידס עצמו הסתייג ממנה ניתן למצוא בכך שהוא מוכיח את עשרים ושמונה הטענות הראשונות ב"יסודות" בלי להזדקק לה. מורכבותה החריגה של אקסיומת המקבילים הביאה למאמצים רבים, במשך כאלפיים שנה, להוכיח שהיא נובעת מהאקסיומות האחרות, כך שלא יהיה צורך להניחה בנפרד. המאמצים להוכחת האקסיומה עלו בתוהו, עד שבראשית המאה התשע-עשרה הבינו בויאי, לובצ'בסקי וגאוס שנדרש כיוון שונה. כתוצאה מכך פותחו גאומטריות לא אוקלידיות, שבהן אקסיומת המקבילים מוחלפת באקסיומה אחרת. כך למשל:

• בגאומטריה ההיפרבולית- דרך כל נקודה שמחוץ לישר עוברים אינסוף ישרים מקבילים לישר זה.
• בגאומטריה ספירית כל שני ישרים על פני הספירה נפגשים בנקודה כלשהי (אין ישרים מקבילים).

גאומטריות אילו אינן רק מושגים מדעיים מופשטים, אלא הן מתקבלות במידה והמשטח עליו נמצאת הצורה אינו מישורי.

לערך המלא

5

השאלה האם P=NP היא בעיה פתוחה מרכזית במדעי המחשב, העוסקת ביכולת לפתור אוסף גדול של בעיות בצורה יעילה. במילים פשוטות, השאלה היא האם כל בעיה שניתן לבדוק עבורה בצורה יעילה האם פתרון מוצע הוא נכון (בעיה השייכת לקבוצה NP), היא גם בעיה שניתן למצוא עבורה פתרון בצורה יעילה (בעיה השייכת לקבוצה P). לפתרון הבעיה ישנן השלכות תאורטיות ומעשיות רבות, והיא זכתה להכרה כאחת מ"שבע בעיות המילניום" של מכון קליי למתמטיקה. אף שכיום לא ידועה תשובה לשאלה זו, ההשערה הרווחת היא כי P≠NP.

השאלה האם P=NP אינה בעלת ערך אקדמי בלבד. עם התפתחות השימושים המסחריים של ההצפנה בעידן המחשב, ובמיוחד במסחר אלקטרוני, הפכה התשובה לשאלה לבעלת חשיבות כלכלית לא מבוטלת. הסיבה לכך היא שרוב המסחר האלקטרוני ותעשיית האבטחה הדיגיטאלית מסתמכים על אלגוריתמים שיכולת ההצפנה שלהם נובעת מחוסר היכולת הנוכחי לפתור בעיות NP בזמן סביר.

לערך המלא

6

משפט ארבעת הצבעים הוא תוצאה בולטת בהיסטוריה של הטופולוגיה הקומבינטורית ושל תורת הגרפים. לפי המשפט, אפשר לצבוע כל מפה מדינית, באופן שכל שתי מדינות בעלות קו גבול משותף נצבעות בצבע שונה, תוך שימוש בארבעה צבעים בלבד. מתמטיקאים החלו לחקור את הבעיה באמצע המאה התשע-עשרה. היא נודעה כ'השערת ארבעת הצבעים', וזכתה ל'הוכחות' שגויות רבות.

צביעה הדורשת לפחות ארבעה צבעים

בניסוח מודרני, המשפט מבטיח שלכל גרף מישורי קיימת צביעת קודקודים בארבעה צבעים. אנשי תורת הגרפים מכירים הוכחות קלות יחסית לכך שקיימת צביעה בחמישה צבעים, אבל ההוכחה לכך שאפשר להסתפק בארבעה נמצאה רק ב- 1976, והיא כרוכה בחיפוש ממוחשב על-פני אלפי מקרים. זו הייתה ההשערה המפורסמת הראשונה שהוכחה בעזרת מחשב, ובתחילה לא הייתה הסכמה כללית על תקפות ההוכחה, בעיקר בנימוק שלא הוכחה נכונותן של תוכניות המחשב עצמן. מאז נעשו ניסיונות רבים למצוא הוכחה סטנדרטית יותר, שיכולה לעמוד לביקורת עמיתים. הוכחה כזו עדיין לא נמצאה.

האיור משמאל מציג מפה סכמטית של ארבע מדינות, שלכל אחת מהן יש גבול משותף עם כל האחרות. לכן לא ניתן לצבוע אותה בפחות מארבעה צבעים.

לערך המלא

7

השערת רימן היא השערה שהציע בשנת 1859 המתמטיקאי ברנרד רימן, מגדולי המתמטיקאים של אותה עת. לפי ההשערה, החלק הממשי של כל האפסים (הלא טריוויאליים) של פונקציה מרוכבת הידועה בשם "פונקציית זטא של רימן" הוא $\ {\frac {1}{2}}$. השערה זו, הקשורה קשר עמוק להתפלגות של המספרים הראשוניים, היא מן הבעיות הפתוחות הבולטות ביותר בתורת המספרים ובמתמטיקה בכלל.

לערך המלא

8

הבעיות הגאומטריות של ימי קדם הן בעיות בנייה שנוסחו על ידי היוונים הקדמונים, והעסיקו מתמטיקאים במשך מאות שנים. הבעיות הן:

• בניית קובייה שנפחה כפול מזה של קובייה נתונה
• שילוש זווית: חלוקת זווית נתונה לשלושה חלקים שווים
• בניית ריבוע השווה בשטחו לעיגול נתון
• בניית מצולע משוכלל בן שבע צלעות

את כל הבניות יש לבצע במסגרת כללי המשחק של הגאומטריה, כלומר באמצעות בנייה בסרגל ובמחוגה בלבד.

רק במאה התשע-עשרה הושם קץ לניסיונות לפתור בעיות בנייה אלה, כאשר הוכח בעזרת תורת גלואה שהן לא פתירות, כלומר אין דרך לבצע את הבניות הנדרשות. עד למועד זה תרמו הניסיונות לפתרון בעיות אלה להתפתחותה של הגאומטריה.

לערך המלא

9

השערת הראשוניים התאומים קובעת שישנם אינסוף זוגות של ראשוניים תאומים, כלומר מספרים $\ p,p+2$ ששניהם ראשוניים. השערה זו היא אחת מן הבעיות הפתוחות המפורסמות בתורת המספרים ובמתמטיקה בכלל.

מתמטיקאים מאמינים שאכן ישנם אינסוף זוגות של ראשוניים תאומים, בגלל שורה של נימוקים היוריסטיים המבוססים על תכונות סטטיסטיות של המספרים הראשוניים, ובגלל עדויות מספריות התומכות בהשערת הארדי-ליטלווד. עם זאת, להשערה עדיין אין הוכחה.

לערך המלא

10

משפט ארבעת הריבועים של לגראנז' הוא מן התוצאות הקלאסיות והאלגנטיות בתורת המספרים. המשפט, אותו הוכיח ז'וזף לואי לגראנז' ב-1770, קובע שכל מספר טבעי אפשר לכתוב כסכום של ארבעה ריבועים: לכל מספר טבעי n אפשר למצוא מספרים שלמים a,b,c,d, כך ש- $\ n=a^{2}+b^{2}+c^{2}+d^{2}$. לדוגמה, $\ 107=8^{2}+5^{2}+3^{2}+3^{2}$.

לערך המלא

11

אי-שוויון הממוצעים הוא אי-שוויון מפורסם הקושר בין הממוצע החשבוני והממוצע גאומטרי של סדרה סופית של מספרים. זהו אי-שוויון בסיסי באנליזה מתמטית, ויש לו שימושים חשובים והכללות רבות. את אי-השוויון גילה והוכיח אוגוסטן לואי קושי, וברבות השנים התגלו עשרות הוכחות אחרות.

באותו שם נקרא גם אי שוויון בין הממוצע ההנדסי לממוצע ההרמוני; יחדיו, טוענים שני אי-השוויונות שלכל קבוצה $\ a_{1},\dots ,a_{n}$ של מספרים ממשיים חיוביים, מתקיים

${\frac {n}{{\dfrac {1}{a_{1}}}+\cdots +{\dfrac {1}{a_{n}}}}}\leq {\sqrt[{n}]{a_{1}\cdots a_{n}}}\leq {\frac {a_{1}+\cdots +a_{n}}{n}}$

כלומר הממוצע ההרמוני קטן או שווה לממוצע ההנדסי, והממוצע ההנדסי קטן או שווה לממוצע החשבוני. בשני המקרים לא מתקיים שוויון, אלא אם כל המספרים $a_{1},\ldots ,a_{n}$ שווים זה לזה.

לערך המלא

12

משפט החתונה, שמיוחס למתמטיקאי פיליפ הול, הוא משפט בקומבינטוריקה, שנותן תנאי הכרחי ומספיק לבחירת נציגים ייחודיים עבור משפחה של קבוצות.

נניח שיש לנו קבוצת נשים וקבוצת גברים וכל אישה מעוניינת בקבוצה חלקית כלשהי של הגברים. נשאלת השאלה, באילו תנאים ניתן לשדך לכל אישה גבר שהיא מעוניינת בו (באופן מונוגמי כמובן). ברור כי תנאי הכרחי הוא שמספר הגברים יהיה לפחות כמספר הנשים. ניתן להכליל דרישה זו לכל קבוצת נשים. כלומר, תנאי הכרחי הוא שכל $\!\,k$ נשים תהינה מעוניינות בלפחות $\!\,k$ גברים. משפט הול טוען כי תנאי זה הינו גם תנאי מספיק. נוסח לא פורמלי (אם כי מדויק לחלוטין) זה הוא שהעניק למשפט את כינויו.

לערך המלא

13

השערת גולדבך היא השערה בתורת המספרים, שלפיה כל מספר זוגי גדול מ-4 ניתן להציג כסכום של שני מספרים ראשוניים.

השערת גולדבך נבדקה באמצעות מחשב ונמצאה נכונה לכל מספר עד $\ 2\cdot 10^{17}$. ההערכה המקובלת היא שההשערה נכונה, בהתבסס על התפלגותם של המספרים הראשוניים: ככל שמספר זוגי גדול יותר, כך סביר יותר שניתן להציגו כסכום של שני ראשוניים. מובן שזו אינה הוכחה.

לערך המלא

14

משפט המינימקס הוא משפט בתורת המשחקים העוסק במשחק סכום אפס סופי לשני שחקנים. (משחק סכום אפס הוא משחק שבו הרווח של כל משתתף מאוזן במדויק על–ידי ההפסד של המשתתפים האחרים). המשפט קובע כי לכל משחק מסוג זה קיימת דרך פעולה אופטימלית לשחק מבחינת שני השחקנים, כך שהרווח המינימלי של כל אחד אינו תלוי במעשי השני. המשפט הוכח בשנת 1928 על ידי ג'ון פון נוימן. משפט המינימקס נקרא כך כיוון שכל שחקן שואף למקסם את התשלום המינימלי שהוא יכול לקבל מהמשחק, או למזער ("למנם") את ההפסד המקסימלי.

לערך המלא

15

משפט רייס הוא משפט מרכזי בתחום החישוביות, שעוסק ביכולת של אלגוריתמים לחקור אלגוריתמים אחרים. המשפט קובע שאין תוכנית מחשב שמקבלת כקלט תוכנית מחשב אחרת, ומכריעה האם הפונקציה שמחשבת תוכנית מחשב זו היא בעלת תכונה מסוימת "לא-טריוויאלית" או לא. (כלומר, תכונות אשר מאפיינות חלק מהפונקציות שמחושבות בידי תוכנית מחשב, אך לא את כולן) יש לשים לב שהתכונה היא תכונה של הפונקציה, ולא של תוכנית המחשב עצמה. באופן אינטואיטיבי המשפט טוען שתוכנית מחשב אינה יכולה לדעת מה תוכנית מחשב אחרת עושה (כי אז היא הייתה צריכה להריץ אותה, וזה שקול לבעיית העצירה).

לערך המלא

16

אי-שוויון ברנולי הוא אי-שוויון יסודי ושימושי באנליזה מתמטית, המאפשר להעריך את הביטוי $\ (1+x)^{n}$. האי-שוויון קובע ש- $\ (1+x)^{n}\geq 1+nx$ לכל מספר שלם $\ n\geq 0$ ולכל מספר ממשי $\ x>-1$. את האי-שוויון אפשר להוכיח באינדוקציה.

בעזרת אי-שוויון זה אפשר להראות שהסדרה $\ \left(1+{\frac {1}{n}}\right)^{n}$ עולה בזמן שהסדרה $\ \left(1+{\frac {1}{n}}\right)^{n+1}$ יורדת, וכך להגדיר את בסיס הלוגריתם הטבעי, $\ e=2.718...$, כגבולן המשותף.

לערך המלא

17

המשפט היסודי של החשבון הדיפרנציאלי והאינטגרלי (נקרא גם המשפט היסודי של החשבון האינפיניטסימלי) קושר בין שני מושגי היסוד של החשבון האינפיניטסימלי, הנגזרת והאינטגרל, ומראה שגזירה ואינטגרציה הן פעולות הופכיות זו לזו: אם פונקציה רציפה עוברת אינטגרציה ואחר כך גוזרים את התוצאה, חוזרים לפונקציה המקורית. פרט לקשר זה, המשפט גם מספק שיטה מעשית לחישוב האינטגרל המסוים, שהוא מושג שמוגדר בצורה שאינה מאפשרת חישוב פשוט, באמצעות האינטגרל הלא מסוים, שלחישובו יש דרכים רבות.

המשפט היסודי של החשבון האינפיניטסימלי קובע שאינטגרל מסוים בין שתי נקודות שווה להפרש הערכים של האינטגרל הלא המסוים שלה בנקודות אלו. לכאורה שני מושגים אלה שונים זה מזה ובאים מעולמות שאין להם שום קשר אבל המשפט היסודי של החשבון האינפיניטסימלי (שנקרא גם משפט ניוטון-לייבניץ) קובע את הקשר העמוק בין שני התחומים.

לערך המלא

18

בתמונה זו m=9 ולכן כאשר נתונות עשר יונים, על שתיים מהן לחלוק תא אחד.

עקרון שובך היונים, או בשמו השני: "עקרון דיריכלה", הוא עיקרון מתמטי הקובע כי אם יש m תאים בשובך שלתוכם יש להכניס m+1 יונים, קיים בהכרח תא אחד שבו תימצאנה לפחות שתי יונים. לעיקרון טריוויאלי זה יש שימושים רבים בהוכחות בתחום הקומבינטוריקה, וניתן להוכיח באמצעותו תוצאות רבות, מעניינות ולא-טריוויאליות כלל.

בניסוחו הפורמלי בתורת הקבוצות, המשפט קובע שאם עוצמת הקבוצה A גדולה ממש מעוצמת הקבוצה B, אזי לא קיימת פונקציה חד-חד-ערכית מ-A ל-B.

^{(ראו גם: חידה שבפתרונה נעשה שימוש בעקרון שובך היונים.)}

לערך המלא

19

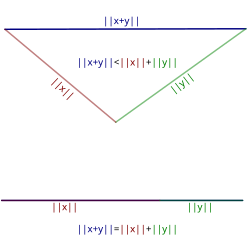
אי שוויון המשולש הוא התרגום האלגברי לעובדה שבמשולש, אורכה של כל צלע קטן מסכום ארכי הצלעות האחרות. אי-שוויון המשולש מבטא את העובדה שלא ניתן לקצר את הדרך מ- A ל- C על ידי מעבר בנקודה B (כלומר: הקו הישר הוא הדרך הקצרה ביותר בין שתי נקודות). בצורתו הפשוטה, עבור זוג מספרים $\ x$ ו- $\ y$, מתקיים $\ |x+y|\leq |x|+|y|$.

זוהי תכונה יסודית כל-כך של מושג ה"מרחק", עד שהיא מהווה אחת מהאקסיומות המגדירות מטריקה ומרחב מטרי. לפיכך, אי שוויון זה נכון, בהכללה, עבור כל נורמה (המושג "נורמה" הוא הכללה של מושג ה"אורך"). בפרט, אי שוויון המשולש האינטגרלי הוא גרסה של אי שוויון המשולש עבור הנורמה האינטגרלית.

לערך המלא

20

השערת ארדש-שטראוס נוסחה על ידי המתמטיקאים פול ארדש וארנסט ג. שטראוס בשנת 1948 אם כי ההופעה המוקדמת ביותר שלה בספרות היא במאמר של ארדש מ-1950.

ההשערה קובעת שעבור כל מספר טבעי $n\geq 2$, המספר הרציונלי ${\frac {4}{n}}$ ניתן לביטוי כסכום של בדיוק שלושה שברים יסודיים. כלומר, קיימים שלושה מספרים טבעיים x, ‏y ו-z, כך שמתקיים: ${\frac {4}{n}}={\frac {1}{x}}+{\frac {1}{y}}+{\frac {1}{z}}\qquad \,$ . אם נכפיל משווה זו ב-nxyz נקבל את הצורה השקולה $\ 4xyz=n(xy+xz+yz)$, שהיא ניסוח של ההשערה כמשוואה דיופנטית.

אם n הוא מספר פריק, $n=pq$, אז ניתן למצוא פיתוח של ‎4/n בקלות באמצעות הפיתוחים של ‎4/p או ‎4/q. לכן, אם קיימת דוגמה נגדית להשערת ארדש-שטראוס, המספר, n, הקטן ביותר שיצור דוגמה נגדית יהיה ראשוני.

אנשים רבים נעזרו במחשבים כדי לחפש דוגמה נגדית להשערה באמצעות שימוש בכוח גס. נכון לאוקטובר 1999, חיפושים מסוג זה, של אלאן סווט (פרופסור למתמטיקה באוניברסיטה של אינדיאנפוליס), אימתו את ההשערה עבור כל n טבעי עד ל-$10^{14}$.

לערך המלא

21

משפט בולצאנו-ויירשטראס באנליזה מתמטית קובע כי לכל סדרה אינסופית חסומה של נקודות ב-$\mathbb {R} ^{n}$ קיימת תת-סדרה מתכנסת. ניסוח אחר (ושקול) של המשפט קובע כי לכל קבוצה אינסופית חסומה של נקודות ב-$\mathbb {R} ^{n}$ קיימת נקודת הצטברות.

הרעיון האינטואיטיבי שעומד מאחורי המשפט הוא שאם קיימת קבוצה שיש בה אינסוף נקודות, והאיברים שלה לא יכולים "לברוח" רחוק מדי, לפחות חלק מהם אמורים להיות קרובים מאד זה לזה. המשפט מראה בצורה קונסרקטיבית כיצד ניתן למצוא את הסדרה או נקודת ההצטברות המבוקשות, אך זו אינה דרך מעשית, מאחר שהיא מבוססת על תהליך אינסופי של חלוקת הקטע החסום לחלקים קטנים והולכים.

לערך המלא

22

משפט ארדש-סקרש במתמטיקה דיסקרטית הוא משפט הקובע כי בכל סדרה באורך $\ ab+1$ של מספרים ממשיים שונים יש תת-סדרה עולה באורך $\ a+1$ או תת-סדרה יורדת באורך $\ b+1$. המשפט הדוק - הטענה אינה נכונה עבור סדרה כללית באורך $\ ab$.

המשפט הוא מטיפוס רמזי - אין אי סדר מוחלט - בתוך כל ים גדול דיו של כאוס יש איים של סדר.

את המשפט הוכיחו פאול ארדש וגאורגה סקרש, במאמר שפרסמו בשנת 1935.

לערך המלא

23

השערת קולץ היא בעיה בתורת המספרים, הקשורה בהתייצבות של התהליך המספרי הבא:

מגדירים כלל, באופן הבא: מספרים זוגיים יש לחלק בשתיים, בעוד שמספרים אי-זוגיים יש להכפיל בשלוש ולהוסיף לתוצאה אחת. ההשערה היא שהפעלה חוזרת של כלל זה תביא בסופו של דבר למספר 1, ואין זה משנה מהי נקודת ההתחלה. לדוגמה, הפעלת התהליך על המספר 11 מביאה ל-34, משם ל-17, ואחר-כך, לפי הסדר, $\ 52\rightarrow 26\rightarrow 13\rightarrow 40\rightarrow 20\rightarrow 10\rightarrow 5\rightarrow 16\rightarrow 8\rightarrow 4\rightarrow 2\rightarrow 1$. בדוגמה זו, כמו במקרים רבים אחרים, מתקבלים מספרים גדולים יחסית, אך בסופו של דבר הירידות מתגברות על העליות, והתוצאה מגיעה ל-1.

השערה זו זכתה לפופולריות רבה, בעיקר משום שקל מאד לתכנת ולבדוק אותה בעזרת מחשב. ההשערה נבדקה עבור מספרים עד ל-27 מיליון מיליארדים, אבל לא ידועה לה עדיין כל הוכחה. פול ארדש אמר על השערה זו כי "המתמטיקה עדיין לא מוכנה לבעיות כאלה", ואף הציע, כדרכו, פרס כספי בן 500 דולר למי שימצא לה הוכחה.

לערך המלא

24

משפט פיתגורס הוא משפט מפורסם בגאומטריה, המתאר את היחס בין שלוש צלעותיו של משולש ישר-זווית. המשפט קובע כי ”סכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר זווית, שווה לשטח הריבוע הבנוי על היתר” (הניצבים הם שתי צלעות שביניהן כלואה הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם $\ a$ ו-$\ b$, ואורך היתר הוא $\ c$, אז: $\ a^{2}+b^{2}=c^{2}$.

המשפט נקרא על שם המתמטיקאי והפילוסוף היווני פיתגורס, שחי במאה ה-6 לפנה"ס, אשר נהוג לייחס לו את ההוכחה הכללית הראשונה של המשפט, אם כי אין ודאות שהוא אכן זה שהוכיחו.

לערך המלא

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

---

< בחזרה לפורטל