פורטל:מתמטיקה/מאמר נבחר/אוסף

עריכהערך מומלץ

1

איור המציג את שבעת השלבים הראשונים בבניית קבוצת קנטור

קבוצת קנטור היא קבוצה שנבנית בצורה האיטרטיבית הבאה: לוקחים קטע ישר, ומסירים ממנו את השליש האמצעי. מבצעים פעולה דומה בכל אחד משני הקטעים שנותרו, ונשארים עם ארבעה קטעים, שגם עליהם ממשיכים את התהליך, וכך הלאה עד אינסוף.

קבוצה זו תוארה בידי המתמטיקאי גאורג קנטור בשנת 1883. חשיבותה הרבה היא בתכונותיה המיוחדות, שסותרות את האינטואיציה ומציגות מעט ממורכבותו ומייחודו של האינסוף. תכונות אלה דחפו את קנטור לפתח את תורת הקבוצות. קרוב למאה שנים מאוחר יותר נמנתה קבוצת קנטור עם הקבוצות שעליהן ביסס בנואה מנדלברוט את רעיון הפרקטל.

לערך המלא

2

פלימפטון 322

פלימפטון 322 הוא שמו של לוח חרסית שמקורו בבבל והוא מתוארך בין השנים 1900 לפנה"ס עד 1600 לפנה"ס. הלוח, הכתוב בכתב יתדות, מכיל ארבע עמודות וחמש עשרה שורות של מספרים בספרות בבליות, כך שהמספרים בשתיים מן העמודות שייכים לשלשות פיתגוריות. מהות המספרים שבו שנויה במחלוקת - על פי חלק מהפרשנויות, הלוח שימש לייצור שלשות פיתגוריות או לחישוב ערכה של פונקציה טריגונומטרית ובכך הוא מעיד על רמה מתמטית גבוהה של התרבות הבבלית.

הלוח התגלה בעת חפירות ארכאולוגיות לא חוקיות, יחד עם עוד אלפי לוחות מסוגו, בשנות העשרים של המאה ה-20. ג.א. פלימפטון קנה את הלוח, ככל הנראה מבלי שהוא או המוכר יבחינו בייחוד שבו, ובשנות ה-30 תרם אותו יחד עם האוסף שלו לאוניברסיטת קולומביה, שם הוא שמור עד עצם היום הזה.

לערך המלא

3

האריתמטיקה והרטוריקה. פסלם של ניקולא וג'ובאני פיסאנו, פונטנה מאג'ורה, פראג

אריתמטיקה (מהמילה היוונית "אריתמוס" שמשמעותה מספר) היא הענף העתיק והבסיסי ביותר במתמטיקה. חוקי האריתמטיקה הבסיסיים משמשים כל אדם מודרני לצורך ביצוען של משימות יום-יומיות פשוטות כגון הכנת מזון ותכנון כלכלת הבית. לאריתמטיקה המתקדמת יותר ולתחומים הקרובים אליה, הכוללים פעולות מתמטיות מסובכות, יש שימוש רב בתחומי המדע, ההנדסה והטכנולוגיה השונים.

במובנה המצומצם, המילה מתייחסת לענף במתמטיקה העוסק בפעולות הקשורות במספרים, כגון ארבע פעולות החשבון או פעולות מורכבות יותר. מתמטיקאים משתמשים לעתים במונח "אריתמטיקה" כתחליף לתורת המספרים. גבולותיו של ענף מתמטי זה אינם תחומים באופן חד, והם השתנו במרוצת השנים. באופן עקרוני, עוסקת האריתמטיקה במספרים, ביצוע פעולות עליהם, חקירת המאפיינים שלהם וסוגיהם, ובאלגוריתמים ומושגים בעלי קרבה רעיונית או תוכנית לתחום זה. כך, למשל, משתמשים לעתים במונח "אריתמטיקה" גם לצורך חקירת מספרים ראשוניים או בעיות חישוביות שונות בגאומטריה אלגברית.

לערך המלא

4

חשבונייה סינית

האריתמטיקה היא הענף העתיק ביותר במתמטיקה ואחד השימושיים שבו לצורכי יום-יום. ההיסטוריה של האריתמטיקה משתרעת על פני תקופות שונות, תרבויות ומקומות שונים בהם התפתח ענף זה. בחלק מהמקרים היו אלה התפתחויות שנצברו על סמך ניסיון רב-שנים ובחלק מהמקרים היו אלה פירות מחקר של מתמטיקאים בודדים. עד לעת החדשה התפתחה האריתמטיקה באופן שונה באזורים גאופוליטיים שונים, ולפיכך כרוכה היסטוריה זו גם בהיסטוריה הדתית, החברתית והגאופוליטית של מקומות אלה. כך, למשל, עם כיבוש הבבלים את מסופוטמיה, ירשו אלה את השימוש בבסיס 60 מקודמיהם האשורים. כדוגמה נוספת, רוחבית, ניתן להסתכל על מושג האפס. פיתוחו, כפי שהוא מוכר היום, עבר שלבים רבים והושפע רבות מהקשיים התפיסתיים, הדתיים והפילוסופיים שעורר בתרבויות השונות.

לערך המלא

5

ארבע פעולות החשבון הן פעולות החשבון הבסיסיות ביותר, השימושיות בחיי היומיום של מרבית בני האדם. פעולות אלה נלמדות בתחילת לימודי המתמטיקה בבית הספר היסודי, וחרף פשטותן היחסית, נדרשת לביצוען מידה מסוימת של הפשטה.

ארבע פעולות החשבון הן חיבור, חיסור, כפל וחילוק. כל אחת מפעולות אלה היא פעולה בינארית, כלומר פונקציה הפועלת על שני מספרים, אך ניתן לכתוב ביטויים הכוללים מספרים רבים ופעולות רבות. במקרה זה נחוצים כללים לקביעת סדר ביצוע הפעולות (פעולה קרויה גם אופרטור, ומספרים שעליהם היא פועלת קרויים אופרנדים). הכלל הראשון קובע שפעולות כפל וחילוק קודמות לפעולות חיבור וחיסור. כדי לבצע את הפעולות בסדר שונה מהאמור בכלל זה יש להשתמש בסוגריים. לאחר שני כללים אלה, הפעולות מתבצעות משמאל לימין.

באלגברה מופשטת מעוניינים לחקור את תכונותיהן של פעולות שמוגדרות על קבוצות כלשהן, לא בהכרח של מספרים, אך שמזכירות את פעולות החשבון על המספרים.

לערך המלא

6

המלון של הילברט הוא סיפור שבו השתמש המתמטיקאי הנודע דויד הילברט בהרצאות פופולריות שנתן, והוא בא להמחיש בצורה נאה את התכונות המיוחדות של קבוצות אינסופיות, תכונות מפתיעות למדי למי שמורגל לעסוק רק בקבוצות סופיות.

הסיפור מדבר על בית מלון, שחדריו ממוספרים בסדר עולה: 1, 2, 3, וכו'. להבדיל ממלון רגיל, מספר החדרים במלון זה הוא אינסופי, כלומר לכל מספר טבעי קיים במלון חדר שזה מספרו (קבוצת המספרים הטבעיים היא קבוצה אינסופית אך בת מנייה, כלומר ניתן למנות את אבריה לפי סדרם).

הסיפור מתחיל כאשר כל החדרים במלון תפוסים ואורח חדש, ω, מגיע.

לערך המלא

7

השער להדפסה הראשונה של יסודות באנגלית, 1570

יסודות (ביוונית: Στοιχεῖα) הוא חיבור בן שלושה עשר חלקים, שנכתב על ידי המתמטיקאי ההלניסטי אוקלידס בראשית המאה השלישית לפנה"ס. בספר מאורגנים באופן שיטתי הגדרות, אקסיומות ומשפטים בגאומטריה, בתורת המספרים ובאלגברה בסיסית. "יסודות" הוא הספר הקדום ביותר מסוג זה ששרד עד ימינו, והייתה לו השפעה מכרעת על התפתחותם של הלוגיקה, המתמטיקה והמדע בכלל.

הספר נחשב לאחד הספרים המצליחים ביותר שנכתבו מאז ומעולם. עותקים של הספר הגיעו מביזנטיום לארצות ערב, ואז תורגמו מערבית ללטינית במאה ה-12. "יסודות" הודפס לראשונה בוונציה ב-1482, במהדורה המבוססת על עותק של ג'ובאני קמפנו משנת 1260, וזכה מאז ליותר מאלף מהדורות דפוס. בין המהדורות ראוי לציון תרגום לעברית שנעשה בעידודו של הגאון מווילנה (האג, תק"ם 1780). מספר עותקים של הטקסט היווני שרדו עד ימינו, ומצויים למשל בספריית הוותיקן ובאוקספורד. עותקים אלה אינם שלמים, ונדרשת עבודה רבה כדי לשחזר את המקור ברמת מהימנות גבוהה.

לערך המלא

8

משחק מגדלי האנוי עשוי עץ לבוד

מגדלי האנוי (באנגלית: Towers of Hanoi) הוא משחק חידה מתמטי, שמקורו בסוף המאה ה-19. המשחק הוא אמצעי הדגמה פופולרי לעקרון הרקורסיה ולמושגים בסיסיים אחרים בקומבינטוריקה ובמדעי המחשב.

המשחק כולל שלושה מוטות אנכיים ("המגדלים") ומספר דיסקיות בגדלים שונים שניתן להשחיל על המוטות. בתחילת המשחק, הדיסקיות מסודרות על פי הגודל על אחד המוטות, כשהגדולה ביותר למטה והקטנה ביותר למעלה.

מטרת המשחק היא להעביר את כל הדיסקיות למוט אחר, תחת שני החוקים הללו:

• מותר להזיז רק דיסקית אחת בכל פעם - כלומר להוציאה מהמוט שבו היא נמצאת, ולהשחיל אותה על מוט אחר.
• אסור לשים דיסקית על דיסקית שקטנה ממנה.

כאשר מקודדים כללים אלה בצורה גרפית, מתקבלת גרסה סופית של משולש סיירפינסקי.

לערך המלא

9

מערכות המספרים החשובות וקשרי ההכלה ביניהן

במתמטיקה, מערכת מספרים היא קבוצה של מספרים, או עצמים הדומים למספרים, שמוגדרות בה פעולות אריתמטיות כגון חיבור וכפל. המערכות החשובות ביותר הן קבוצת המספרים הטבעיים, חוג המספרים השלמים, שדה המספרים הרציונליים, שדה המספרים הממשיים ושדה המספרים המרוכבים. עם זאת לשאלה 'מהי מערכת מספרים' אין תשובה מדויקת, וקבוצות כלליות יותר עשויות להחשב למערכות מספרים בהקשר המתאים.

סביר להניח שבתחילה רק מספרים טבעיים נחשבו כ'מספרים'. אלו הם מונים של קבוצות סופיות: אחד, שניים, שלושה, ארבעה וכן הלאה. בבית הספר של פיתגורס 'מספר' היה תמיד יחס בין שני מספרים שלמים, כלומר (בשפה המודרנית) מספר רציונלי. מצד שני הפיתגוראים זיהו מספר עם האורך של קטע מתאים, והעדיפו בזה את הגישה הגאומטרית לשאלה 'מהו מספר'. הצורך של הפיתגוראים בהתאמה בין שתי ההגדרות האלה היה חזק כל-כך, עד שלפי האגדה הם זרקו לנהר תלמיד שגילה כי אורך האלכסון של ריבוע שצלעו יחידה אחת (שורש 2 על-פי משפט פיתגורס) אינו מספר רציונלי.

לערך המלא

10

המחשה של ערכו של פאי בקירוב

במתמטיקה, $\pi$ (האות היוונית פִּי, או פַּאי לפי ההיגוי האנגלי) מייצגת את היחס הקבוע (בגאומטריה האוקלידית) בין היקף המעגל לקוטרו. $\pi$ הוא קבוע מתמטי שמופיע בנוסחאות רבות במתמטיקה ובפיזיקה. הערך מסומן כ-π משום שהוא משמש לחישוב היקף מעגל: האות π היא הראשונה במילה היוונית περιφερεια (פריפריה) שמשמעותה היקף. האות $\pi$ נקראת במקור "פִּי", אך עקב הקריאה שלה באנגלית, מקובל בישראל לקרוא לה "פאי".

ארבעים הספרות הראשונות של $\pi$ הן: 3.1415926535897932384626433832795028841971

לערך המלא

11

משולש על משטח בגאומטריה היפרבולית. פיתוח הגאומטריה הלא אוקלידית העקבית במאה ה-19 הדגיש את חשיבותו של השימוש באקסיומות כנגד החשיבה האינטואיטיבית.

הפילוסופיה של המתמטיקה היא ענף של הפילוסופיה העוסק בהנחות היסוד של המתמטיקה ובמשמעותה של המתמטיקה. הפילוסופיה של המתמטיקה מנסה לתת תשובות לשאלות כגון:

• "האם המתמטיקה היא תגלית או המצאה?"
• "מדוע המתמטיקה שימושית בתיאור היקום?"
• "באיזה מובן, אם בכלל, ישויות בסיסיות של המתמטיקה, כמו מספרים, קיימות?"
• "האם משפטים מתמטיים נכונים ובאיזה אופן?"

לערך המלא

12

‏‏

הדגמת הטענה "סכומם של n המספרים האי-זוגיים הראשונים הוא המספר הריבועי העומד במקום n".

אינדוקציה מתמטית היא שיטה לוגית המאפשרת להוכיח שתכונה מסוימת משותפת לכל המספרים הטבעיים. האינדוקציה מורכבת משני טיעונים: ראשית, שהמספר 1 מקיים את התכונה, ושנית, שאם מספר טבעי n מקיים אותה, אז גם המספר n+1 מקיים אותה. עקרון האינדוקציה מחליף סדרה אינסופית של הוכחות סופיות (אחת לכל מספר טבעי), בהוכחה סופית אחת המספיקה לכל המקרים.

את המונח "אינדוקציה מתמטית" הציע הלוגיקן אוגוסטוס דה-מורגן, כשכתב את הערך "אינדוקציה (מתמטיקה)" בציקלופדיית פני ב-1838. השיטה עצמה הופיעה בצורתה המודרנית אצל בלז פסקל (1654), אם כי אפשר לזהות ניצנים של השיטה אצל מתמטיקאים שקדמו לו.

גמישותה של שיטת האינדוקציה הפכה אותה לאחד מכלי ההוכחה החזקים ביותר בארגז הכלים של כל מתמטיקאי.

לערך המלא

13

חידות חיתוך והרכבה הן חידות העוסקות בדרכים שבהן ניתן לחתוך צורה למספר צורות אחרות, לדרכים שבהן ניתן לקחת חלקים ולחבר אותם יחד לצורה חדשה, וכן בחידות המשלבות את שתי הפעולות: כיצד ניתן לחתוך צורה נתונה על מנת להרכיב צורה אחרת מחלקיה.

חידת חיתוך קלאסית

חידת חיתוך קלאסית היא כיצד ניתן לחלק את הצורה הנקראת L-tromino לשניים, שלושה וארבעה חלקים זהים (בתמונה נראה הפתרון לחלוקה ל-4 חלקים).

חידת ההרכבה המפורסמת ביותר היא הטנגרם, ובה ריבוע מחולק ל-7 חלקים שמהם ניתן להרכיב מגוון רב של צורות הכוללות אנשים, בעלי חיים וצמחים. חידה דומה מסוג זה, הנקראת 'סטומכיוון' נחקרה על ידי המדען והמתמטיקאי היווני ארכימדס. המתמטיקאי ההודי הגדול אריאבהטה השתמש בשיטות של חיתוך והרכבה על מנת להוכיח את משפט פיתגורס (הוכחה שנלמדת עד היום בבתי הספר) ולאחריו הופיעו הוכחות רבות נוספות המשתמשות גם הן בחיתוך והרכבה.

לערך המלא

14

באנליזה מתמטית, זהות אוילר, הקרויה על שמו של המתמטיקאי השווייצרי הידוע לאונרד אוילר, היא השוויון הבא:

$e^{\pi i}+1=0$

כל אברי הזהות הם מספרים קבועים:

• e הוא בסיס הלוגריתם הטבעי.
• π הוא היחס בין היקף המעגל לקוטרו.
• i הוא היחידה המדומה, מקיים: $i^{2}=-1$

זהות אוילר נחשבת בעיני רבים כזהות יוצאת דופן בשל יופיה המתמטי, הנובע מהפעולות הבסיסיות שהיא משלבת בתוכה (חיבור, כפל והעלאה בחזקה) ומהקבועים המתמטיים הבסיסיים שהיא מקשרת ביניהם.

לערך המלא

15

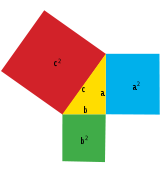
משפט פיתגורס הוא משפט גאומטרי, הנחשב לאחד המשפטים המתמטיים הנודעים ביותר. הוא קובע שסכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר (הניצבים הם שתי צלעות הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם $\ a$ ו-$\ b$, ואורך היתר הוא $\ c$, אז: $\ a^{2}+b^{2}=c^{2}$. המשפט ההפוך, הקובע שמשולש שבו ריבוע צלע אחת שווה לסכום ריבועי הצלעות האחרות הוא ישר-זווית, נכון גם הוא.

המשפט נקרא על שם המתמטיקאי והפילוסוף היווני פיתגורס, שחי במאה ה-6 לפנה"ס על אף שאת המשפט עצמו הכירו בתרבויות עתיקות מאות שנים לפני זמנו.

בעיה מפורסמת מתורת המספרים היא מציאת משולשים ישרי זווית שאורכי הצלעות שלהם הינם מספרים שלמים, כלומר למצוא פתרונות שלמים למשוואה הדיופנטית: $\ a^{2}+b^{2}=c^{2}$. שלשה של מספרים כאלה קרויה שלשה פיתגורית, וידוע שיש אינסוף שלשות מסוג זה. דוגמה לשלשה פיתגורית הם המספרים 3,4,5 שכן הם מקיימים את המשוואה: $\ (9+16=25)\quad 3^{2}+4^{2}=5^{2}\quad$.

לערך המלא

16

הנחות היסוד לציור בפרספקטיבה

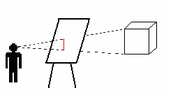
גאומטריה פרויקטיבית היא גאומטריה לא אוקלידית, שבה אקסיומת המקבילים מוחלפת באקסיומה אחרת: כל שני ישרים במישור נפגשים בנקודה.

הגאומטריה הפרויקטיבית נולדה מתוך הצרכים המעשיים של אמני הציור. לעומת הציור הרוחני והסמלי של ימי הביניים, לקראת הרנסאנס עלתה קרנו של הציור המדויק – הדומה לנראה בעין. החייאת הכתבים הקלאסיים והאמונה שבבסיס הטבע עומדים עקרונות מתמטיים, הובילה את הציירים והמתמטיקאים בני התקופה לנסות ולמצוא שיטה סדורה לציור העולם התלת-ממדי על בד ציור דו-ממדי.

האמנים הראשונים בתחום זה שמשנתם ידועה לנו היו פיליפו ברונלסקי ולאונה בטיסטה אלברטי, שחיבר את הטקסט הראשון (הידוע כיום) בנושא, שכותרתו "על הציור" – De pictura. אנשי מפתח מאוחרים יותר בתחום זה הם פיירו דלה פרנצ'סקה, לאונרדו דה וינצ'י, אלברכט דירר ואחרים.

המתמטיקאי ז'ראר דזרג (Gérard Desargues) היה ממניחי היסודות התאורטיים לגאומטריה הפרויקטיבית, ועסק בה יחד עם בלז פסקל.

לערך המלא

17

כתב החידה מתוך ספרו של ז'ול ורן "מסע אל בטן האדמה"

קריפטוגרפיה היא ענף במתמטיקה ובמדעי המחשב העוסק באלגוריתמים של אבטחת מידע על רבדיה השונים, ובביסוס המתמטי שלהם. תחום הקריפטוגרפיה מאגד תחתיו נושאים רבים ובהם: הצפנה של מידע חסוי ממי שלא הוסמך לראותו; אימות זהות (כמו באמצעות סיסמה) ובקרת הרשאות גישה; פרוטוקולים להוכחת ידיעה, כמו פרוטוקול אתגר מענה והוכחה באפס ידע; מנגנוני חתימה דיגיטלית לאימות זהות המקור ומניעת התכחשות, והבטחת שלמות המידע.

קריפטוגרפיה מודרנית נמצאת בשימוש ביישומים מעשיים רבים, החל מאבטחת רשתות תקשורת (גם אלחוטיות כמו רשת סלולרית), דרך דואר אלקטרוני, מסחר אלקטרוני, כרטיסי אשראי ואבטחת מסופי משיכת מזומנים.

לערך המלא

18

$\ \int _{C}\quad \oint _{C}$

אינטגרל קווי (לעתים גם אינטגרל לאורך עקום, אינטגרל מסלולי או אינטגרל מסילתי) הוא אינטגרל המחושב לאורך מסילה במרחב, ולאו דווקא לאורך קטע ממשי. כמו האינטגרל הרגיל, האינטגרל הקווי מסכם ערכים של פונקציה נתונה ומשקלל אותם לפי אורך המסילה, באופן המכליל סיכום של מספר סופי של ערכים. הפונקציה שאת האינטגרל שלה מחשבים עשויה לקבל ערכים ממשיים, או ערכים וקטוריים בכל מרחב בנך (ובכלל זה המרחב האוקלידי).

הצורך באינטגרל קווי עולה בעת ניתוח גדלים הקשורים בתנועה במסלול שאינו ישר, או בתכונות פיזיקליות של גוף עקום, כגון חוט דק. בדרך זו, ניתן לחשב גדלים כדוגמת אורך, מסה, או מטען חשמלי. האינטגרל הקווי מחשב כוח הפועל על גוף המיוצג על ידי עקום, או עבודה של כוח המניע מסה לאורכו, כמו גם התנהגות של שדות פיזיקליים (למשל, שדה חשמלי) על פני מסלולים.

לאינטגרלים קוויים של פונקציות אנליטיות או הרמוניות ישנן תכונות מתמטיות הקושרות אותם לערכי הפונקציה במשטח שאותו סוגר העקום. בקשרים אלה עוסקים כמה משפטים באנליזה מרוכבת, באנליזה וקטורית ובאנליזה הרמונית.

לערך המלא

19

$\ 2^{3}=8$ $\ e^{i\pi }=-1$ $\ 2^{\aleph _{0}}=\aleph$

חזקה היא פעולה מתמטית המתבצעת בין שני מספרים ומסומנת $\ a^{b}$. בצורתה הבסיסית ביותר, כאשר $\ n$ הוא מספר טבעי, החזקה $\ a^{n}$ שווה ל-$\ n$ מופעים של $\ a$ הנכפלים זה בזה. את ההגדרה הבסיסית הזו ניתן להרחיב למערכות מספרים רבות, ואף לעצמים מתמטיים שאינם בהכרח מספרים, תוך שמירה על תכונותיה הבסיסיות הייחודיות של הפעולה, הנקראות חוקי חזקות.

לחזקה תפקיד מרכזי בתחומים רבים במתמטיקה. השערות ומשפטים הקשורים בפעולה העסיקו מתמטיקאים במשך מאות שנים. פונקציות המבוססות על פעולת החזקה, כגון פולינומים ופונקציות מעריכיות, משמשות בכל תחומי המדעים. בשל כך פותחו שיטות המאפשרות חישוב חזקות באופן יעיל, במקום הכפלה חוזרת שעשויה לקחת זמן רב.

לערך המלא

20

גאורג קנטור

משפט קנטור הוא משפט מתמטי יסודי בתורת הקבוצות. באופן פורמלי, המשפט קובע שהעוצמה של כל קבוצה קטנה מהעוצמה של קבוצת התת-קבוצות שלה. משמעות המשפט היא שלכל קבוצה, אפילו אינסופית, יש קבוצה גדולה ממנה (במובן מדויק שיוגדר בהמשך). מסקנה מיידית היא שיש אינסוף גדלים אינסופיים השונים זה מזה, ואין אינסוף גדול ביותר.

את המשפט הגה והוכיח אבי תורת הקבוצות, גאורג קנטור, בשנת 1891. שיטת הלכסון אותה המציא כדי להוכיח את המשפט ותוצאות דומות, מנצלת את הסתירות שביסוד פרדוקס הסַפָּר ופרדוקס השקרן, ומשמשת בתחומים רבים החורגים מתורת הקבוצות.

לערך המלא

---

< בחזרה לפורטל