נוסחת אוילר (אנליזה מרוכבת)

נוסחת אוילר היא נוסחה יסודית באנליזה מרוכבת, הקושרת את הפונקציה המעריכית הטבעית המרוכבת לפונקציות הטריגונומטריות סינוס וקוסינוס. הנוסחה נקראת על-שמו של לאונרד אוילר.

הנוסחה קובעת כי: $e^{i\theta }=\cos \theta +i\sin \theta$ לכל $\theta$ ממשי, כאשר e הוא בסיס הלוגריתם הטבעי ו-i הוא היחידה המדומה. את $\cos \theta +i\sin \theta$ יש הנוהגים לסמן בצורה המקוצרת $cis\theta$.

לנוסחה שימושים רבים, בין היתר היא מסייעת בפתרון משוואות דפרנציאליות לינאריות עם מקדמים קבועים, שלהן יישומים רבים בפיזיקה ובהנדסה.

זהות אוילר

ערך מורחב – זהות אוילר

כאשר מציבים בנוסחה את $\pi$ כערכה של הזווית $\theta$, מתקבל: $e^{i\pi }=-1$ או $e^{i\pi }+1=0$, תוצאה הקרויה זהות אוילר ומקשרת בצורה פשוטה בין 5 קבועים מתמטיים בסיסיים.

הקשר להצגה קוטבית

הצגה גאומטרית של נוסחת אוילר

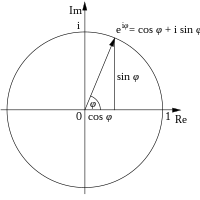
בהינתן מספר מרוכב $z$ השונה מאפס, ניתן למתוח קטע $l$ במישור המרוכב בין ראשית הצירים לנקודה $z$. האורך של $l$, $r$, מכונה הערך המוחלט של $z$, ואילו הזווית (ברדיאנים) בין הכיוון החיובי של הציר הממשי ל-$l$ (נגד כיוון השעון), $\theta$, מכונה הארגומנט של $z$. הזוג $(r,\theta )$ מכונה ההצגה הקוטבית של $z$.

אם נציג את $z$ בצורה $z=x+iy$, אז $x$ ו-$y$ הם אורכי הניצבים במשולש ישר-זווית שיתרו הוא $l$. לפי הגדרת הפונקציות הטריגונומטריות מתקיים $x=r\cos \theta$ ו-$y=r\sin \theta$. לכן לפי נוסחת אוילר:

$z=x+iy=r(\cos \theta +i\sin \theta )=r{e}^{i\theta }$

הצגה זו של מספר מרוכב נוחה לשימוש במקרים רבים. למשל כאשר כופלים אותם: $z_1\cdot z_2=r_1{e}^{i{\theta }_1}\cdot r_2{e}^{i{\theta }_2}=r_1{r}_2{e}^{i({\theta }_1+{\theta }_2)}$.

מסקנה מיידית מהצגה זו היא משפט דה-מואבר הקובע כי $(\cos x+i\sin x{)}^n=\cos (nx)+i\sin (nx)$ ל-n טבעי ו-x ממשי. לפי נוסחת אוילר זהו פשוט השוויון $(e^{ix}{)}^n=e^{i(nx)}$.

משמעות אלגברית

מנוסחת אוילר נובע שההעתקה $f(x)=e^{ix}=\cos x+i\sin x$ היא הומומורפיזם של חבורות מן הישר הממשי כחבורה ביחס לפעולת החיבור, אל מעגל היחידה במישור המרוכב כחבורה ביחס לפעולת הכפל. זהו אפימורפיזם שאיננו איזומורפיזם שכן $f(x)=f(x+2\pi )$.

הגרעין של $f$ הוא הקבוצה $2\pi \mathbb{\mathbb{Z}}$ ולכן לפי משפט האיזומורפיזם הראשון מעגל היחידה איזומורפי ל-$\mathbb{ℝ}/2\pi \mathbb{\mathbb{Z}}$, או אחרי נרמול $\mathbb{ℝ}/\mathbb{\mathbb{Z}}$.

הוכחות

קיימות מספר הוכחות לנוסחה, שמתבססות על ההגדרה של פונקציית האקספוננט המרוכבת לפי טור טיילור של הפונקציה הממשית או כפונקציה המקיימת את התכונות הידועות של הפונקציה הממשית.

באמצעות טור טיילור

זוהי הוכחה של נוסחת אוילר באמצעות פיתוח טור טיילור וכן העובדות הבסיסיות אודות החזקות של $i$:

$\begin{array}{rlrlrlrl}{i}^{4n}& =1,& i^{4n+1}& =i,& i^{4n+2}& =-1,& i^{4n+3}& =-i\end{array}$

לכל n שלם. אפשר לבטא את הפונקציות הממשיות $e^x$,‏ $\cos (x)$ ו-$\sin (x)$ באמצעות פיתוח טור טיילור שלהן סביב 0:

$\begin{array}{rl}{e}^x& =1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \\ \cos x& =1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots \\ \sin x& =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots .\end{array}$

עבור מספרים מרוכבים נגדיר את הפונקציות האלה באמצעות הטורים הללו, על ידי החלפת המספר הממשי $x$ במספר המדומה $i\theta$ (כאשר $\theta$עצמו ממשי).

לפי הגדרה זאת אפשר לראות ש:

$\begin{array}{rl}{e}^{i\theta }& =1+i\theta +\frac{(i\theta {)}^2}{2!}+\frac{(i\theta {)}^3}{3!}+\frac{(i\theta {)}^4}{4!}+\frac{(i\theta {)}^5}{5!}+\frac{(i\theta {)}^6}{6!}+\frac{(i\theta {)}^7}{7!}+\frac{(i\theta {)}^8}{8!}+\cdots \\ & =1+i\theta -\frac{{\theta }^2}{2!}-\frac{i{\theta }^3}{3!}+\frac{{\theta }^4}{4!}+\frac{i{\theta }^5}{5!}-\frac{{\theta }^6}{6!}-\frac{i{\theta }^7}{7!}+\frac{{\theta }^8}{8!}+\cdots \\ & =(1-\frac{{\theta }^2}{2!}+\frac{{\theta }^4}{4!}-\frac{{\theta }^6}{6!}+\frac{{\theta }^8}{8!}-\cdots )+i(\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}-\frac{{\theta }^7}{7!}+\cdots )\\ & =\cos \theta +i\sin \theta \end{array}$

(החלפת סדר האיברים מוצדקת משום שכל הטורים מתכנסים בהחלט).

באמצעות חשבון דיפרנציאלי

נגדיר את הפונקציה $f(x)$, במשתנה ממשי $x$, בתור:

$f(x)=(\cos x+i\sin x)\cdot e^{-ix}$

הנגזרת של (f(x, לפי חוק המכפלה, היא:

$\begin{array}{rl}\frac{d}{dx}f(x)& =(\cos x+i\sin x)\cdot \frac{d}{dx}{e}^{-ix}+\frac{d}{dx}(\cos x+i\sin x)\cdot e^{-ix}\\ & =(\cos x+i\sin x)(-i{e}^{-ix})+(-\sin x+i\cos x)\cdot e^{-ix}\\ & =(-i\cos x-i^2\sin x)\cdot e^{-ix}+(-\sin x+i\cos x)\cdot e^{-ix}(i^2=-1)\\ & =(-i\cos x+\sin x-\sin x+i\cos x)\cdot e^{-ix}\\ & =0\end{array}$

לכן, $f(x)$ חייבת להיות פונקציה קבועה ביחס ל-$x$. משום ש-$f(0)$ ידוע, הקבוע ש- $f(x)$ שווה אליו עבור כל $x$ ממשי גם ידוע. כלומר:

$(\cos x+i\sin x)\cdot e^{-ix}=f(x)=f(0)=(\cos 0+i\sin 0)\cdot e^0=1$.

על ידי הכפלת שני הצדדים ב-$e^{ix}$ ושימוש בשוויון

$(\cos x+i\sin x)\cdot e^{-ix}\cdot e^{ix}=1\cdot e^{ix}$

נקבל כי:

$e^{ix}=\cos x+i\sin x$.

הכללות

ניתן להכליל את נוסחת אוילר מהמספרים המרוכבים אל הקווטרניונים על ידי הנוסחה $\exp (xr)=\cos x+r\sin x,$ כאשר r הוא נקודה על כדור היחידה התלת-ממדי במרחב הקווטרניונים ה-4 ממדי הנקרא ורסור.

קישורים חיצוניים

מדיה וקבצים בנושא נוסחת אוילר בוויקישיתוף

• גדי אלכסנדרוביץ', נוסחת אוילר, ואיך היא קשורה למתנד הרמוני, באתר "לא מדויק", 6 באפריל 2010
• נוסחת אוילר (אנליזה מרוכבת), באתר אנציקלופדיה למתמטיקה (באנגלית)
• נוסחת אוילר, באתר MathWorld (באנגלית)
• נוסחת אוילר, באתר אנציקלופדיה בריטניקה (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

נוסחת אוילר (אנליזה מרוכבת)39441068Q184871