משפט הסיבובים של אוילר

סיבוב המיוצג על ידי ציר וזווית אוילר.

בגאומטריה, משפט הסיבובים של אוילר קובע שבמרחב תלת-ממדי, כל שינוי אוריינטציה של גוף קשיח שיש לו נקודת שבת (נקודה הנותרת קבועה במקומה), שקול לסיבוב יחיד מסביב לציר מסוים שעובר דרך נקודת השבת. פירוש הדבר הוא גם שכל הרכבה של שני סיבובים היא גם סיבוב, כאשר "סיבוב" מוגדר כאיזומטריה עם נקודת שבת בראשית הצירים. המשפט מראה לפיכך שכל האברים בחבורת הסיבובים התלת-ממדית הם סיבובים.

המשפט קרוי על שמו של לאונרד אוילר, אשר הוכיח אותו ב-1775 בשיטות של גאומטריה כדורית. ציר הסיבוב השקול נקרא ציר אוילר, והוא מיוצג בדרך כלל על ידי וקטור היחידה ê. ההרחבה של המשפט הזה לקינמטיקה מולידה את המושג של ציר סיבוב רגעי; ישר של נקודות שבת. משפט זה של אוילר הוא משפט נקודת השבת הראשון שנתגלה.

משפט זה נכון רק בכל מרחב מממד אי-זוגי, אבל לא בממדים זוגיים. בממד זוגי, כמו למשל במקרה של סיבוב במישור, הרכבה של שני סיבובים לא בהכרח מותירה כיוון קבוע מסוים. על כן, כיוון שהמשפט אינו כה מובן מאליו, עולה הצורך לספק לו הוכחה פורמלית וריגורוזית.

במונחים של אלגברה ליניארית, המשפט קובע, שבמרחב תלת-ממדי, כל שתי מערכות קואורדינטות קרטזיות בעלות ראשית משותפת מתקבלות זו מזו על ידי סיבוב מסביב לציר מקובע מסוים. פירוש הדבר הוא גם שמכפלת שתי מטריצות סיבוב היא גם מטריצת סיבוב, ושבעבור מטריצות סיבוב מתקיים שהערך העצמי הראשון שלהם הוא 1 ושהשניים האחרים הם מרוכבים וצמודים זה לזה. הוקטור העצמי המתאים לערך העצמי 1 הוא ציר הסיבוב המקשר בין שתי מערכות הקואורדינטות.

משפט אוילר (1776)

אוילר ניסח את המשפט שלו כדלהלן:

"כאשר ספירה מוסטת מסביב למרכז שלה זה תמיד אפשרי למצוא קוטר אשר כיוונו במיקום המוסט זהה לכיוונו המקורי"

הוכחה

ההוכחה המקורית של אוילר נעזרת בשיטות בנייה מתחום הגאומטריה הכדורית.

איור 1: המעגל הגדול הכחול הופך למעגל הגדול האדום כאשר מסובבים את הכדור בזווית מסוימת מסביב לציר סיבוב שעובר דרך O.

אנליזה מכינה

כדי להוכיח את המשפט, אוילר מנתח תחילה כיצד ייראו הדברים אילו המשפט היה נכון. בהנחה שהקו הצהוב באיור 1 עובר דרך מרכז הכדור והוא ציר הסיבוב שאנו מחפשים, ואילו נקודה O היא אחת משתי נקודות החיתוך של הציר הזה עם הכדור. לאחר מכן הוא מתייחס למעגל גדול שרירותי שלא מכיל את O (המעגל הכחול) ולתמונה שלו תחת הסיבוב (המעגל האדום), שהינה מעגל גדול אחר שלא מכיל את O. הוא מסמן את נקודת החיתוך שלהם כ-A (אם המעגלים מתלכדים, אז A יכולה להיבחר ככל נקודה אחרת; אחרת יש שתי נקודות חיתוך).

איור 2: קשתות שמחברות את הקדם-תמונה α והתמונה a של A. האיור מראה גם את חוצה הזווית AO של הזווית בקודקוד A.

כעת A היא על המעגל ההתחלתי (המעגל הכחול), כך שהתמונה שלה תהיה על מעגל התמונה (המעגל האדום). הוא מסמן את התמונה הזו כ-a, כיוון ש-A היא נקודת החיתוך של שני המעגלים, ועל כן היא גם על מעגל התמונה, המיקום שלה הוא גם התמונה של נקודה אחרת שהייתה על המעגל ההתחלתי (המעגל הכחול) - נקודה זו "תופסת את מקומה" של A, והוא מסמן אותה באות α (ראו איור 2). לאחר מכן הוא מתייחס לשתי הקשתות המחברות את α ו-a עם A. לקשתות הללו יש אותו האורך כיוון שקשת αA מועתקת לקשת Aa. בנוסף, כיוון ש-O היא נקודת שבת, משולש αOA מועתק למשולש AOa, כך שהמשולשים הללו שווי-שוקיים, והקשת AO חוצה את הזווית αAa∠.

בנייה של הנקודה המתאימה ביותר

איור 3: O עוברת ל-O′, אבל O′ חייבת להתלכד עם O.

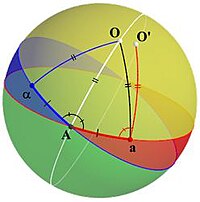
כעת נבנה את הנקודה שתהיה אינווריאנטית תחת הפעולות שתוארו מקודם. נתחיל עם המעגל הגדול הכחול והתמונה שלו תחת הטרנספורמציה, שהוא המעגל האדום הגדול שהופיע באיור 1. תהי A נקודת החיתוך של שני המעגלים הללו. אם התמונה של A תחת סיבוב היא אותה הנקודה אז A היא נקודת שבת של הטרנספורמציה, והקוטר של הכדור שמכיל את A הוא ציר הסיבוב, כך שהמשפט מוכח.

אחרת נסמן את התמונה של A כ-a ואת הקדם-תמונה שלו כ-α, ונחבר את שתי הנקודות הללו עם A באמצעות הקשתות αA ו-Aa. לשתי הקשתות הללו יש אותו אורך. נבנה את המעגל הגדול שחוצה את הזווית αAa∠ ונמקם נקודה O על המעגל הגדול הזה כך שקשתות AO ו-aO יהיו בעלות אותו אורך, כשלאחר מכן נקרא לאזור של הספירה המכיל את O ותחום על ידי המעגל האדום והמעגל הכחול "הפנים של αAa∠ (זהו האזור הצהוב באיור 3). מכיוון ש-αA = Aa ו-O היא על החוצה זווית של αAa∠, אז נקבל גם αO = aO.

הוכחה לאינווריאנטיות של הנקודה תחת הטרנספורמציה

כעת נניח בשלילה שנקודה O אינה הנקודה המבוקשת, כך שקיימת נקודה אחרת ′O שהיא התמונה שלה. אז אנו יודעים ש-αAO′ = ∠AaO∠ ושהאוריינטציה נשמרת כך ש-′O חייבת להיות פנימית ל-αAa∠. כעת AO מועתקת ל-′aO, כך ש-′AO = aO. כיוון ש-AO היא באותו אורך כמו aO, מתקיים AaO = ∠aAO∠. אולם aAO′ = ∠AaO∠, כך ש-∠AaO′ = ∠AaO, ולפיכך ′O היא אותה נקודה כמו O. במילים אחרות, O היא נקודת שבת של הטרנספורמציה, וכיוון שמרכז הכדור הוא גם נקודת שבת, הקוטר של הכדור שמכיל את O הוא ציר הסיבוב.

הערות כלליות על הבנייה

השרטוט המקורי של אוילר.

אוילר מצביע גם על כך ש-O ניתנת לבנייה באמצעות חיתוך האנך האמצעי לקשת Aa עם חוצה הזווית αAO∠, דרך בנייה שעשויה להיות קלה יותר מבחינה מעשית. הוא גם הציע להיעזר בחיתוך של שני מישורים:

• מישור הסימטריה של הזווית αAa∠ (אשר עובר דרך המרכז C), ו-
• מישור הסימטריה של הקשת Aa (שגם עובר דרך C).

טענה: שני המישורים הללו נחתכים לאורך קוטר. קוטר זה הוא זה שאנו מחפשים.

הוכחה: נקרא לאחת משתי נקודות החיתוך של הקוטר עם משטח הספירה O. כיוון ש- αA מועתקת ל-Aa ולמשולשים יש אותן הזוויות, נובע מכך שמשולש OαA מועתק למשולש OAa. לפיכך הנקודה O חייבת להישאר קבועה במקומה תחת הטרנספורמציה.

מסקנות: בנייה זו מראה גם שכל סיבוב של הספירה ניתן להבנה כשני שיקופים עוקבים ביחס לשני המישורים שתוארו לעיל. נקודות במישור הראי הן קבועות תחת שיקוף, ולכן נקודות על החיתוך שלהם (ישר: זהו ציר החיתוך) נשמרות תחת שני השיקופים, ולכן תחת סיבוב.

דרך פשוטה אחרת למצוא את ציר הסיבוב היא להתייחס למישור שעליו נמצאות הנקודות α, A, a. ציר הסיבוב הוא בבירור ניצב למישור הזה, ועובר דרך המרכז C של הספירה.

הוכחה מטריציונית

סיבוב מרחבי הוא העתקה ליניארית שנמצאת בהתאמה חד-חד ערכית עם מטריצת סיבוב R מסדר 3 × 3 אשר מעבירה וקטור קואורדינטות x לוקטור קואורדינטות אחר X, כלומר Rx = X. לפיכך, ניסוח אחר של משפט אוילר הוא שבעבור כל סיבוב R ישנו וקטור שונה מאפס n כך ש-Rn = n; כלומר, זוהי בדיוק הטענה ש-n הוא וקטור עצמי של R השייך לערך העצמי 1. לכן מספיק להוכיח ש-1 הוא ערך עצמי של R; ציר הסיבוב יהיה הישר μn, כאשר n הוא הווקטור העצמי עם ערך עצמי 1.

מטריצות סיבוב הן בעלות התכונה היסודית שהמטריצה ההופכית שלהן היא המטריצה המשוחלפת שלהן, כלומר:

$\mathbf {R} ^{\mathsf {T}}\mathbf {R} =\mathbf {R} \mathbf {R} ^{\mathsf {T}}=\mathbf {I} ,$

כאשר I היא מטריצת היחידה מסדר 3 × 3 והכתיב העליון T מסמל את המטריצה המשוחלפת.

כעת נחשב את הדטרמיננטה של מטריצות הסיבוב הללו כדי לגלות שהן שוות ±1. מתקיים:

$1=\det(\mathbf {I} )=\det \left(\mathbf {R} ^{\mathsf {T}}\mathbf {R} \right)=\det \left(\mathbf {R} ^{\mathsf {T}}\right)\det(\mathbf {R} )=\det(\mathbf {R} )^{2}\quad \Longrightarrow \quad \det(\mathbf {R} )=\pm 1.$

כעת נראה שלמטריצת סיבוב R יש לפחות וקטור אינווריאנטי אחד n, כלומר Rn = n. כיוון שזה מצריך ש-R − I)n = 0), יש להראות det(R − I) = 0. ניעזר בקשר:

$\det(-\mathbf {A} )=(-1)^{n}\det(\mathbf {A} )=-\det(\mathbf {A} )\quad$

בעבור כל מטריצה A מסדר n × n כאשר n אי-זוגי; כיוון שאנו עוסקים בסיבובים תלת-ממדיים, n = 3 והתנאי מתקיים. כמו כן ניעזר בקשר:

$\det \left(\mathbf {R} ^{-1}\right)=1\quad$

(הנובע מכך ש-det(R) = 1 ומהעובדה שהדטרמיננטה היא כפלית) ונקבל:

${\begin{aligned}\det(\mathbf {R} -\mathbf {I} )=\det \left((\mathbf {R} -\mathbf {I} )^{\mathsf {T}}\right)&=\det \left(\mathbf {R} ^{\mathsf {T}}-\mathbf {I} \right)=\det \left(\mathbf {R} ^{-1}-\mathbf {R} ^{-1}\mathbf {R} \right)\\&=\det \left(\mathbf {R} ^{-1}(\mathbf {I} -\mathbf {R} )\right)=\det \left(\mathbf {R} ^{-1}\right)\,\det(-(\mathbf {R} -\mathbf {I} ))=-\det(\mathbf {R} -\mathbf {I} )\quad \Longrightarrow \quad \det(\mathbf {R} -\mathbf {I} )=0.\end{aligned}}$

זה מראה ש-λ = 1 הוא שורש (פתרון) של הפולינום האופייני של R, כלומר ש-:

$\det(\mathbf {R} -\lambda \mathbf {I} )=0\quad {\hbox{for}}\quad \lambda =1.$.

הישר λn הוא אינווריאנטי תחת הפעולה של R, כלומר, λn הוא ציר הסיבוב. זה מוכיח את משפט אוילר.

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

23332081משפט הסיבובים של אוילר