נקודת אמצע קטע

בגאומטריה אוקלידית, נקודת אמצע קטע היא נקודה על קטע, אשר חוצה אותו לשני קטעים שווים.^[1]

נקודת אמצע קטע משמשת בבניות גאומטריות חשובות כגון התיכון, קטע האמצעים ומרכז הכובד.

נקודת אמצע קטע באה לידי שימוש בתחומים שונים כגון פיזיקה, הנדסה, אדריכלות ועוד.

הגדרה מתמטית

בהינתן זוג נקודות $A$ ו- $B$ , הנקודה $M$ תקרא אמצע הקטע $A B$ אם ורק אם מתקיימים שני התנאים הבאים:

הנקודות $A$ ,‏ $B$ ו- $M$ הן קו-ליניאריות (כלומר, שלושתן על ישר אחד משותף).
$A M = B M$ . כלומר, $M$ חוצה את $A B$ לשני קטעים שווים.

ניתן להוכיח שנקודה $M$ זו תמיד קיימת ושהיא יחידה.

תכונות חשובות

משולש

קטע העובר דרך קודקוד המשולש לאמצע הצלע הנגדית לו נקרא תיכון. כל שלושת התיכונים במשולש נפגשים בנקודה משותפת שהיא מרכז הכובד של המשולש, וחותכים זה את זה ביחס של $2 : 1$ , כאשר החלק הארוך יותר קרוב לקודקוד.
משפט התיכון: בהינתן משולש בעל צלעות $a$ ,‏ $b$ ו- $c$ , ותיכון ל- $c$ בעל אורך $m$ , מתקיים השוויון $a^{2} + b^{2} = 2 m^{2} - \frac{1}{2} c^{2}$ .
לכל משולש קיימת אליפסה הנמצאת בתוך המשולש ומשיקה לו בנקודות האמצע של הצלעות שלו. אליפסה זו נקראת אליפסת שטיינר הפנימית.^[2]
קטע העובר דרך זוג נקודות אמצע קטע של צלעות משולש נקרא קטע אמצעים. ניתן להוכיח כי קטע זה מקביל לצלע שמולו ושווה למחצית אורכה.
נקודת אמצע הקטע בין מרכז המעגל החוסם של משולש למפגש הגבהים שלו הוא מרכז מעגל תשע הנקודות.
עבור משולש ישר-זווית, מרכז המעגל החוסם של המשולש היא נקודת אמצע היתר.
עבור משולש שווה-שוקיים, הקטע היוצא מקודקוד הראש למרכז הצלע שמולו מהווה תיכון, חוצה-זווית וגובה לצלע זו.

מרובע

במקבילית, שני האלכסונים נחתכים בנקודת אמצע הקטע שלהם. כלומר, יש להם נקודת אמצע משותפת.
משפט וריניון: אם מחברים את נקודות אמצע הקטע של כל זוג צלעות צמודות במרובע, מתקבלת מקבילית.
ישר ניוטון: לכל מרובע קמור, הישר העובר דרך אמצעי האלכסונים נקרא ישר ניוטון.^[3] ניתן להוכיח כי כל נקודה על קטע זה מחלקת את המרובע לארבעה משולשים כך שסכום השטחים של זוג משולשים הנמצאים זה מול זה שווה לסכום השטחים של זוג המשולשים הנוספים (משפט אן).^[4]

מעגל

נקודת אמצע הקטע של קוטר במעגל היא מרכז המעגל.
לכל מיתר במעגל, הקטע היוצא ממרכז למעגל לאמצע המיתר, מאונך למיתר. קטע זה נקרא אפותם.
אורך הקטע מאמצע מיתר לאמצע הקשת שלו נקרא סגיטה.

חישוב בקואורדינטות קרטזיות

במישור

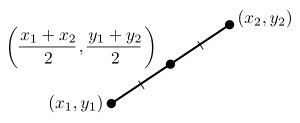
מציאת נקודת האמצע בין שתי נקודות בקואורדינטות קרטזיות

בהינתן מישור אוקלידי בקואורדינטות קרטזיות וזוג נקודות $A = (x_{1}, y_{1})$ ו- $B = (x_{2}, y_{2})$ , ניתן לחשב את נקודות אמצע הקטע בין שתיהן להיות:

$M = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

ניתן להראות כי שלושת הנקודות $A$ ,‏ $B$ ו- $M$ נמצאות על הישר $(x_{2} - x_{1}) y - (y_{2} - y_{1}) x - (x_{2} y_{1} - x_{1} y_{2}) = 0$ . בנוסף:

$\begin{aligned} | A M | = \sqrt{{(x_{1} - \frac{x_{1} + x_{2}}{2})}^{2} + {(y_{1} - \frac{y_{1} + y_{2}}{2})}^{2}} \\ = \sqrt{{(\frac{x_{1} - x_{2}}{2})}^{2} + {(\frac{y_{1} - y_{2}}{2})}^{2}} \\ = \frac{1}{2} \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}} = \frac{1}{2} | A B | \end{aligned}$

באופן זהה, $| M B | = \frac{1}{2} | A B |$ ואכן $M$ חוצה את הקטע $A B$ לשני קטעים שווים.

במרחב כללי

עבור מרחב כללי $n$ ממדי ( $n$ מספר טבעי), בהינתן זוג נקודות $A = (a_{1}, a_{2}, \dots, a_{n})$ ו- $B = (b_{1}, b_{2}, \dots, b_{n})$ , ניתן לחשב את נקודות אמצע הקטע בין שניהם להיות:

$M = (\frac{a_{1} + b_{1}}{2}, \frac{a_{2} + b_{2}}{2}, \dots, \frac{a_{n} + b_{n}}{2})$

חישוב דומה למקרה הדו-ממדי יראה כי אכן $M$ היא מרכז הקטע $A B$ .

בנייה בסרגל ומחוגה

מציאת נקודת מרכז קטע

בהינתן זוג נקודות $A$ ו- $B$ , ניתן לבנות באמצעות סרגל ומחוגה את נקודת אמצע הקטע $M$ :

בונים באמצעות המחוגה מעגל שמרכזו ב- $A$ ועובר דרך $B$ .
בונים באמצעות המחוגה מעגל שמרכזו ב- $B$ ועובר דרך $A$ .
מסמנים ב- $T_{1}$ ו- $T_{2}$ את נקודות החיתוך של שני המעגלים הללו.
מותחים באמצעות הסרגל את הישר $A B$ .
מותחים באמצעות הסרגל את הישר $T_{1} T_{2}$ .
מסמנים את נקודת החיתוך של שני הישרים ב- $M$ .
נקודה $M$ זו היא מרכז הקטע $A B$ .

ניתן להוכיח באמצעות משפט מור-מסקרוני שאפשר למצוא את נקודה $M$ זו גם באמצעות מחוגה בלבד. עם זאת, הדבר דורש שלבים רבים יותר מאשר הבנייה לעיל.

הכפלת קטע

במסגרת בעיות בנייה בסרגל ומחוגה, בהינתן זוג נקודות $A$ ו- $B$ , ניתן למצוא נקודה $C$ כך ש- $B$ היא נקודת אמצע הקטע בין $A$ ל- $C$ .

ניתן לעשות זאת בשתי דרכים:

באמצעות סרגל ומחוגה

להלן אופן מציאת $C$ באמצעות סרגל ומחוגה:

בונים באמצעות המחוגה מעגל שמרכזו ב- $B$ ועובר דרך $A$ .
מותחים באמצעות הסרגל את הישר $A B$ .
מסמנים ב- $C$ את נקודת החיתוך של הישר עם המעגל שאינה הנקודה $A$ .
נקודה $C$ זו היא הכפלת הקטע $A B$ .

באמצעות מחוגה בלבד

להלן אופן מציאת $C$ באמצעות מחוגה בלבד:

בונים באמצעות המחוגה מעגל שמרכזו ב- $A$ ועובר דרך $B$ .
בונים באמצעות המחוגה מעגל שמרכזו ב- $B$ ועובר דרך $A$ .
מסמנים ב- $D$ את אחת מנקודות החיתוך של שני המעגלים.
בונים באמצעות המחוגה מעגל שמרכזו ב- $D$ ועובר דרך $B$ .
מסמנים ב- $E$ את נקודת החיתוך של מעגל זה עם המעגל שמרכזו ב- $B$ שאינה הנקודה $A$ .
בונים באמצעות המחוגה מעגל שמרכזו ב- $E$ ועובר דרך $B$ .
מסמנים ב- $C$ את נקודת החיתוך של מעגל זה עם המעגל שמרכזו ב- $B$ שאינה הנקודה $D$ .
נקודה $C$ זו היא הכפלת הקטע $A B$ .

הכפלת קטע באמצעות מחוגה בלבד היא שלב קריטי בהוכחת משפט מור-מסקרוני. לכל זוג נקודות $A$ ו- $B$ , ולכל מספר טבעי $n$ , ניתן לחזור על בניה זו $n$ פעמים כדי לבנות באמצעות מחוגה בלבד את הנקודה $C_{n}$ על הקרן $\vec{A B}$ כך ש- $\overline{A C_{n}} = n \overline{A B}$ . כלומר, הקטע $A C_{n}$ גדול פי $n$ מהקטע $A B$ .

ראו גם

קישורים חיצוניים

נקודת אמצע קטע, באתר MathWorld (באנגלית)

מחשבון נקודת אמצע קטע של וולפרם אלפא.

הערות שוליים

↑ Eric W. Weisstein, Midpoint, mathworld.wolfram.com (באנגלית)
↑ u/stevephelps, Steiner Inellipse, GeoGebra (באנגלית)
↑ Bimedians in a Quadrilateral, www.cut-the-knot.org
↑ Newton's Theorem and Leon Anne's Theorem, www.cut-the-knot.org

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

נקודת אמצע קטע41949019Q1645406

[1] Eric W. Weisstein, Midpoint, mathworld.wolfram.com (באנגלית)

[2] u/stevephelps, Steiner Inellipse, GeoGebra (באנגלית)

[3] Bimedians in a Quadrilateral, www.cut-the-knot.org

[4] Newton's Theorem and Leon Anne's Theorem, www.cut-the-knot.org

[1]

[2]

[3]

[4]