אפותם

אַפּוֹתֶם של משושה משוכלל

אַפּוֹתֶם (לפעמים מכונה בקיצור אַפּוֹ, ביוונית תמה=להניח) הוא:

במצולע משוכלל

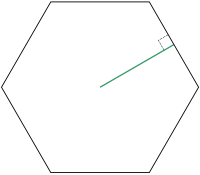
• קטע (או אורכו) ממרכז המצולע לנקודה התיכונה (האמצעית) של אחת הצלעות.
• או באופן שקול, הוא קטע (או אורכו) ממרכז המצולע האנכי לאחת הצלעות. כיוון שהמצולע הוא משוכלל הרי שכל האפותמים שלו חופפים.

במעגל:

• קטע ישר (או אורכו) בין מרכז המעגל לאמצע מיתר על המעגל.
• או באופן שקול, קטע (או אורכו) בין מרכז המעגל האנכי למיתר על המעגל.

בפרמידה משוכללת (פרמידה בעלת בסיס בצורת מצולע משוכלל):

• הקטע הישר (או אורכו) הקצר ביותר בין קודקוד הפרמידה לנקודה על היקף הבסיס (העובר על פני אחת הפאות).

בפירמידה משוכללת קטומה (פירמידה רגולרית שפסגתה נקטמה על ידי מישור המקביל לבסיס):

• האפותם או אורך גובהה של כל פאה טרפזית בצידי הפירמידה הקטומה.

תכונות האפותם

האפותם a יכול לשמש לחישוב השטח של מצולע משוכלל בעל n צלעות באורך s: $A=\frac{nsa}{2}$ אפשר לראות את נכונות הנוסחה אם מחלקים את המצולע ל-n משולשים שווי שוקיים חופפים (עם קודקודי המשולשים במרכז המצולע ועם הבסיסים על צלעות המצולע). שטח משולש הוא מחצית הבסיס כפול הגובה ולכן שטח כל אחד מ-n המשולשים הוא $\frac{sa}{2}$.

$p=ns$ הוא היקף המצולע ולכן ניתן גם לכתוב: $A=\frac{pa}{2}$

האפותם של מצולע משוכלל שווה לרדיוס של המעגל החסום במצולע. לכן הוא גם שווה למרחק המינימלי בין צלע למרכז המעגל. ככל שלמצולע יש יותר צלעות כך שטחו שואף לשטח המעגל החסום, והיקף המצולע p שואף להיקף המעגל החסום $2\pi r$. מכל אלה נובעת הנוסחה לחישוב שטח העיגול: $A=\frac{pa}{2}=\frac{(2\pi r)r}{2}=\pi r^2$

מציאת האפותם

ניתן למצוא את האפותם של מצולע משוכלל במספר דרכים.
האפותם a של מצולע משוכלל בעל n צלעות באורך s ועם רדיוס R למעגל החוסם את המצולע שווה:

$a=\frac{s}{2tan(\frac{\pi }{n})}=Rcos(\frac{\pi }{n})$

ניתן להשתכנע בכך אם מעיינים ב-n המשולשים שווי השוקיים שהוזכרו בדיון למעלה. אם חוצים כל משולש כזה לרוחב מתקבל משולש ישר-זווית בו אורכי הניצבים הם $\frac{s}{2}$ ו- a (האפותם), היתר הוא R והזווית בקודקוד היא $\frac{\pi }{n}$.
האפותם גם שווה ל

$a=\frac{s}{2}tan(\frac{\pi (n-2)}{2n})$

נוסחאות אלו שימושיות גם אם ידועים רק היקף המצולע p ומספר הצלעות n כיוון ש $s=\frac{p}{n}$.

ראו גם

• מצולע משוכלל
• מעגל
• סגיטה

קישורים חיצוניים

מדיה וקבצים בנושא אפותם בוויקישיתוף

• אפותם, באתר MathWorld (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

אפותם41614248Q508490