משוואת ברנולי
משוואת ברנולי היא משוואה בהידרודינמיקה ובאווירודינמיקה המתארת את צורת הזרימה של נוזל או גז ניוטוני. המשוואה פותחה על ידי המתמטיקאי השווייצרי דניאל ברנולי אשר פרסם אותה בשנת 1738 בספרו הידרודינמיקה.
בפשטות, העיקרון מאחורי הנוסחה, הידוע בשם עקרון ברנולי, קובע כי ככל שמהירות זרימתו של זורם (נוזל או גז) על גבי משטח גבוהה יותר, הזורם יפעיל פחות לחץ על המשטח. העיקרון נובע למעשה מחוק שימור האנרגיה, מאחר שסכום האנרגיה הקינטית (שהיא פונקציה של מהירות הזרימה) והאנרגיה הפוטנציאלית הוא קבוע.
משוואת ברנולי קובעת כי:
כאשר:
- – הלחץ בנקודה
- – צפיפות הזורם בנקודה
- – תאוצת הכובד, ערכו בכדור הארץ הוא כ-9.81 מטר לשנייה בריבוע
- – מהירות הזורם בנקודה
- – גובה הזורם בנקודה (ביחס למישור ייחוס שנקבע מראש)
משמעותה של המשוואה היא כי בכל נקודה בזורם סכום ערכי הפרמטרים הוא קבוע. לצורך העניין, לו נבצע שתי מדידות בין הנקודות שהאינדקסים שלהן הם 1 ו־2, אזי יתקבל:
תוקף
נוסחה זו נכונה במסגרת ההנחות הבאות:
- הזורם איננו צמיג, כלומר אין חיכוך פנימי ואין איבוד אנרגיה עקב חיכוך פנימי בין שכבות הזורם.
- הזרימה היא זרימה לוחית יציבה.
- הנוזל הוא אי-דחיס, כלומר צפיפותו קבועה, אך לא בהכרח. כאשר הזורם המדובר הוא כן דחיס, ניתן להכליל את משוואת ברנולי באמצעות שימוש באנתלפיה תרמודינמית.
- המשוואה תקפה לגבי קו הזרימה של הנוזל.
שימושים
בתעופה
עקרון ברנולי הוא למעשה העיקרון החשוב ביותר בהנדסה אווירונאוטית, מאחר שהוא העיקרון שמאפשר למטוס להתרומם מעל פני הקרקע: זרימת האוויר מעל כנף המטוס מהירה יותר מהזרימה מתחת לכנף, ובגלל הפרש המהירויות פועל על כנף המטוס יותר כוח בכיוון מעלה (שמפעיל האוויר מתחת לכנף) מאשר בכיוון מטה (שמפעיל האוויר מעל הכנף), ולכן המטוס מתרומם מהקרקע.
בשיט
עקרון ברנולי הוא הבסיס לתפעול המפרשים המשולשים. על ידי יצירת זרם אוויר מהיר בין שני מפרשים משולשים, ניתן לנצל את עקרון ברנולי ולהניע ספינות מפרש בכיוונים שונים. השימוש במפרשים משולשים שיפר בצורה משמעותית את יכולת הניווט של ספינות, ואיפשר להן לשוט קרוב יותר לכיוון הרוח. החוק התאורטי קובע גבול של עד 45 מעלות אל הרוח, אם כי בעזרת חוקים נוספים ניתן לחדד אל הרוח גם יותר מכך.
בתעשייה
אוחז ברנולי משמש לאחיזה של אובייקטים, ונמצא בשימוש במגוון תחומים בתעשייה.
הוכחת הנוסחה
משוואת ברנולי היא ביטוי לחוק שימור האנרגיה בנוזל אי-צמיג. ניתן להסיקה באמצעות חישוב האנרגיה והעבודה של הנוזל בכל נקודה בקו הזרימה (ראו הוכחה בהמשך). כמו כן, ניתן להסיק את הנוסחה באמצעות פורמליזם של מכניקה אנליטית על משוואות אוילר של זורם.
הוכחת הנוסחה אשר תובא להלן מתבססת על חוק שימור עבודה-אנרגיה הקובע כי עבודת הכוחות הלא משמרים שווה לשינוי בסכום האנרגיה הכוללת. בניסוח מתמטי:
כלומר:
במכניקה הניוטונית מוצג קשר זה בצורה הבאה:
כאשר, בהקשר של זורמים שנפחם הנעים מתנאי לחץ לתנאי לחץ , העבודה היא:
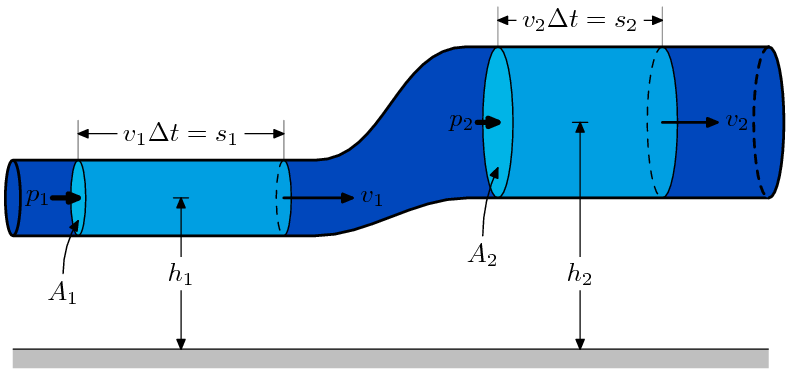
הסבר לטענה האחרונה: לפי השרטוט נתן לראות כי הכח הפועל בכל נקודה הוא כאשר הוא שטח החתך ו- הוא הלחץ באותה הנקודה. האלמנט עובר בזמן נתון העתק של . כמוזכר למעלה, המכפלה של הכח בהעתק נותנת לנו את העבודה. במקרה זה: . היות שמתקיים עבור כל אלמנט והיות והעבודה נעשית במעבר מתנאי לחץ לתנאי לחץ ובניגוד לווקטור הזרימה, שווה העבודה ל־. כאשר לצינור אין צורה המתחלקת בבירור לצורות מנסריות (או בפרט: גליל), ניתן להגיע להצגה זו על ידי מיצוי: חלוקת הצינור לחלקים אינפיניטסימליים אשר צורת כל אחד מהם, בקירוב טוב מאוד, דמוית מנסרה.
ניתן לעשות שימוש בהגדרת הצפיפות כיחס בין מסת הגוף לנפחו – – כדי להציג את השינויים האנרגטיים לפי הצורה
מכאן, מתקבלת הנוסחה:
אחרי צמצום ב- נקבל:
ניתן להציג נוסחה זו בצורה:
או, באופן כללי:
משוואת ברנולי לזרימה פוטנציאלית בלתי יציבה
קיימת וריאציה על משוואת ברנולי שמשמשת במקרים של זרימה לא תמידית; כלומר בזרימה בה וקטור המהירות בנקודה קבועה מסוימת במרחב משתנה בזמן. גרסה זאת של המשוואה משמשת בתאוריה המתמטית של גלי ים ובאקוסטיקה (ניתן לגזור את מהירות הקול על בסיס המשוואה).
בעבור זרימה אי-רוטציונית, מהירות הזורם ניתנת לתיאור כגרדיאנט של פוטנציאל מהירות . במקרה זה, ובעבור צפיפות קבועה , ניתן לעשות אינטגרציה על משוואות התנע והאנרגיה של משוואות אוילר במכניקת הזורמים ולקבל את המשוואה:
שתקפה גם לזרימות לא יציבות. כאן רכיבי המשוואה מסמלים את הנגזרת החלקית של פוטנציאל המהירות לפי הזמן, את האנרגיה הקינטית הסגולית בנקודה (ליחידת מסה), ובאופן דומה שני האיברים האחרונים אנלוגיים ללחץ הזורם ולאנרגיה הפוטנציאלית שלו. הפונקציה תלויה רק בזמן ולא במקום. כתוצאה, משוואת ברנולי ברגע מסוים לא תקפה רק לאורך קו זרם מסוים, אלא בכל תחום הזורם. ניתן גם להציב כביכול את הפונקציה על אפס באמצעות שילובה בפונקציית הפוטנציאל באמצעות הטרנספורמציה:
מה שמניב את הצורה הבאה של המשוואה:
צורה זאת של המשוואה, שכללית יותר מהגרסה היציבה הנפוצה יותר, שימושית מאוד בניתוח בעיות רבות (המקרה הפרטי של זרימה יציבה מתקיים כאשר פוטנציאל המהירות לא משתנה בזמן).
גזירת המשוואה
מבחינה היסטורית, משוואת ברנולי לזרימה פוטנציאלית בלתי יציבה קדמה לניסוח של משוואות אוילר הכלליות יותר, על כן לא מפתיע שמנקודת מבט מודרנית היא נובעת בנקל ממנה. המשוואה נובעת מהמשוואה השנייה בשלוש משוואות אוילר לזורמים (שמייצגת שימור תנע). כדי להוכיח זאת נראה את השקילות בין המשוואות במקרה של זרימה דו-ממדית במישור אנכי. נכתוב את משוואת אוילר לשימור תנע בזורמים:
משוואה זאת חלה על זרימה חד-ממדית. כדי שתהיה ישימה לזרימה דו-ממדית בשדה כבידתי, יש ליישם אותה לקו זרם מסוים, תוך התחשבות בעובדה שהכוחות שפועלים על אלמנט זורם אינם נובעים רק מהפרשי לחצים אלא גם מרכיב כוח הכובד המשיק לקו הזרם. לשם כך נתייחס לקו זרם בפרמטריזציה טבעית; קואורדינטת ה־ של נקודה עליו תהיה אורך העקום מנקודת ההתייחסות עד אליה. בנוסף, כדי לחשב את התאוצה של הזורם בנקודה מסוימת במרחב, נוסיף את האיבר לאיבר התאוצה. כעת, נבצע אינטגרל קווי לפי על משוואת אוילר המתוקנת ונקבל את הקשר:
כאשר הוא הגובה של נקודה ביחס לגובה הייחוס, והמעבר האחרון נובע מההגדרה של פוטנציאל הזרימה:
יישום המשוואה להרחבת חוק טוריצ'לי

 ערך מורחב – חוק טוריצ'לי
ערך מורחב – חוק טוריצ'לי
משוואת ברנולי לזרימה יציבה מאפשרת להסיק את חוק טוריצ'לי, הקובע שמהירות היציאה של המים שווה למהירות הנפילה של גוף הנופל נפילה חופשית מגובה ששווה לעומק הפיה של המכל יחסית למפלס המים במכל: . אולם בפועל, לוקח לתהליך הפריצה של המים זמן סופי להתייצב על מהירות הזרימה שחוזה חוק טוריצ'לי. בסעיף זה נבצע אנליזה כללית יותר, שמאפשרת לחשב גם את הזמן האופייני שחולף עד לקבלת זרימה יציבה. נניח שהפיה היא בעלת אורך , עומק מתחת לפני המים, שטח חתך קטן בהרבה משטח המכל, ונניח שהיא סגורה על ידי מגופה, אשר פותחים אותה ברגע
משוואת ברנולי לזרימה פוטנציאלית בלתי יציבה מאפשרת לקחת בחשבון את האינרציה הסופית של הזורם בפיה. נתייחס לפוטנציאל הזרימה בנקודה על החתך של הפיה. הנגזרת הזמנית שלו שווה לתאוצת המים בפיה כפול אורך הפיה , שכן הזרימה בתוך המכל עצמו זניחה. כיוון שהזרימה מתרחשת בגובה אחיד, משוואת ברנולי לזרימה פוטנציאלית בלתי יציבה מקבלת את הצורה:
פתרון משוואה זאת הוא:
ניתן לכתוב אותו גם כך:
- ,
כאשר הוא הזמן האופייני להתייצבות הזרימה. כאשר מנקבים את דופן הבקבוק (כלומר כאשר אין לו "פיה"), הוא עובי הדופן של הבקבוק.
ראו גם
קישורים חיצוניים
- ד"ר אבי סאייג, עקרון ברנולי: האמת והתפיסות השגויות, במדור "שאל את המומחה" באתר של מכון דוידסון לחינוך מדעי, 15 בפברואר 2017
- משוואת ברנולי, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים
משוואת ברנולי40805853Q181328


