חיכוך

דיאגרמה המתארת את כוח החיכוך הפועל בין שני גופים

במכניקה, חיכוך הוא כוח הפועל באזור המגע של שני גופים הנמצאים במגע זה עם זה, ופועל באופן שמתנגד לתנועה יחסית בין הגופים, או לנטייה לתנועה כזו. הכוח נוצר כאשר על שני הגופים פועלת מערכת של שני כוחות ניצבים זה לזה: כוח ניצב לשטח המגע, הלוחץ את הגופים זה לזה (כוח שנוצר בדרך כלל כתגובה לכוח הכובד), וכוח נוסף, הפועל על אחד הגופים במקביל לאזור המגע. כוח החיכוך הוא למעשה כוח תגובה לכוח המקביל, והפוך לכיוון תנועת הגוף. גודלו המרבי של כוח החיכוך תלוי בגודל הכוח הניצב ובסוג החומר ממנו עשויים שני הגופים. לחיכוך יש השלכות טכנולוגיות רבות, והמדע העוסק בחקר החיכוך, השחיקה והשימון נקרא טריבולוגיה (Tribology).

סימון

באופן כללי כוח החיכוך מסומן כך: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_\mathrm{f}\,} כאשר האות F הגדולה מציינת שמדובר בכוח והאות f הקטנה היא קיצור של המילה חיכוך באנגלית - Friction.

ישנם מספר סוגים של כוחות חיכוך. כאשר רוצים להתייחס לכוח חיכוך ספציפי, מחליפים את האות הקטנה f, באות אחרת המייצגת את אותו הסוג.

לדוגמה: חיכוך סטטי - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_s\,} , חיכוך קינטי - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_k\,} .

מאפיינים

מטאורים נשרפים בשל החיכוך בכניסתם לאטמוספירת כדור הארץ, משום שהעבודה שכוח החיכוך עושה הופכת לחום.

כוח החיכוך הקינטי אינו כוח משמר, כלומר במערכת בה יש חיכוך קינטי אין שימור אנרגיה, והעבודה שכוח החיכוך עושה הופכת לחום או לשינוי צורה של המשטח (דפורמציה פלסטית).

לכך יש היבטים טכנולוגיים רצויים וגם לא רצויים.

• היבטים לא רצויים - החום הנוצר מחיכוך בוכנה של מנוע יכול לגרום להתכה חלקית שלה, השחיקה היא הגורמת לבלאי של חלקי מכונות ולסתימת צינורות.
• היבטים רצויים - החום הנוצר מחיכוך ראש הגפרור גורם להצתתו. למעשה, חיכוך הוא הדרך הפרימיטיבית המקובלת ביותר להצתת אש. דרכים שונות להצתת אש באמצעות חיכוך היו ידועות עוד בתקופת האבן הקדומה, ועודן משמשות בימינו. בנוסף, השחיקה הנגרמת על ידי חיכוך מנוצלת לליטוש של עדשות, החיכוך שהרצפה מפעילה על הרגל שלנו דוחפת אותה קדימה ובעצם מאפשרת לנו ללכת.

מקדם החיכוך

הכוח הנורמלי הוא כוח שמפעיל המשטח בתגובה לכוח שהגוף מפעיל עליו. בתרשים ניתן לראות כיצד שיפוע המשטח משפיע על כמות כוח הכבידה שהגוף מפעיל על המשטח ואת ההשפעה שלו על הכוח הנורמלי.

מקדם החיכוך מתאר את היחס בין כוח החיכוך הפועל בין שני גופים לבין הכוח המצמיד אותם אחד לשני.

באופן כללי מקדם החיכוך מיוצג על ידי האות היוונית μ. כאשר רוצים להתייחס למקדם החיכוך של סוג מסוים נהוג לצרף אות קטנה המייצגת את הסוג הספציפי. לדוגמה:

• מקדם חיכוך קינטי - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_k \,}
• מקדם חיכוך סטטי - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_s \,}

הכוח הנורמלי הוא כוח שמפעיל משטח בתגובה לכוח שמופעל עליו. על כן הוא שווה בגודלו לכוח הפועל בין שני הגופים (או בין גוף למשטח). הוא מסומן באופן מסורתי באות $\ N$, או כ- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_\mathrm{n}\,} .

על כן: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = \frac{F_\mathrm{f}}{N}}

משום שהוא מבטא יחס בין שני כוחות, מקדם החיכוך הוא גודל חסר ממד, כלומר גודל ללא יחידות פיזיקליות - מספר טהור.

השפעת מקדם החיכוך על עצמת כוח החיכוך

מתוך משוואת מקדם החיכוך ניתן לראות ש:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_f = \mu N\,}

כלומר, כוח החיכוך מושפע מגודל מקדם החיכוך, כך שככל שמקדם החיכוך גדל כך גדל גם כוח החיכוך.

השפעת סוג החומר על מקדם החיכוך

שימוש בחומר סיכה להפחתת מקדם החיכוך כחלק מהתחזוקה השוטפת של ציוד מכני

גודלו של מקדם החיכוך משתנה בהתאם לחומרים שמהם עשויים הגופים.

בעקבות זאת, ניתן לשנות את גודלו של כוח החיכוך בין גוף למשטח על ידי הוספה של חומר חוצץ ביניהם המשפיע על גודלו של מקדם החיכוך. שינוי זה יכול להוביל להפחתה או הגברה של כוח החיכוך בהתאם לצורך.

הפחתת כוח החיכוך

חומר סיכה הוא חומר שנועד להפחית את מקדמי החיכוך הסטטים והדינאמים שבין שני משטחים שלפחות אחד מהם נע ונוגעים אחד בשני. להלן מספר דוגמאות:

• אחד השימושים הנפוצים ביותר לשמן סיכה הוא כשמן מנוע. חומר זה מגן על המרכיבים הפנימיים של המנוע מפני שחיקה והתחממות יתר.
• ציפוי של כלי בישול כמו מחבתות וסירים בטפלון מונע את הידבקות המזון אל הכלי.

הגברת כוח החיכוך

ניתן לעשות שימוש בחומרים בעל מקדם חיכוך גבוה לצורך מניעת החלקה. פעולה זו יכולה להגביר את הבטיחות במקומות בהם אנשים עלולים להיפצע כתוצאה מהחלקה. להלן מספר דוגמאות:

• ריצוף רצפת האמבטיה או המקלחת במרצפות מונעות החלקה.
• הוספה של חומר בעל מקדם חיכוך גבוה לתחתית הגרביים כדי למנוע החלקה על הרצפה של הבית.
• קרצוף הכביש באזורים של סיבובים מסוכנים, כדי להעלות את מקדם החיכוך ובכך למנוע החלקת כלי הרכב אל מחוץ לכביש.

סוגי חיכוך

מבדילים בין סוגים שונים של תצורות בהן כוח החיכוך מופיע: חיכוך סטטי, חיכוך קינטי, חיכוך גלגול, גרר.

חיכוך קינטי

שגיאה ביצירת תמונה ממוזערת:

כוח החיכוך הקינטי תמיד מנוגד לכיוון התנועה ביחס למשטח.

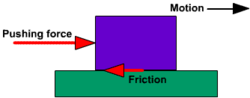
חיכוך קינטי (Kinetic friction) הוא כוח החיכוך בין גופים הנמצאים בתנועה אחד ביחס לשני. כוח החיכוך הקינטי מקביל למשטח שמפעיל אותו על הגוף ומנוגד לכיוון התנועה.

גודלו של כוח החיכוך הקינטי שווה למקדם החיכוך הקינטי כפול הכוח הנורמלי שהמשטח מפעיל על הגוף. כלומר:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_k = \mu_k N\,}

כתוצאה מכך, עצמתו של כוח החיכוך הקינטי קבועה לכל אורך תנועתו של הגוף על אותו המשטח (או על משטח אחר בעל מקדם חיכוך זהה), כל עוד אין שינוי בשיפוע (אשר יכול להשפיע על גודלו של הכוח הנורמלי).

חיכוך סטטי

כוח החיכוך הסטטי אינו קבוע בגודלו. הוא גדל בתגובה לכוח חיצוני המופעל על הגוף. כאשר הכוח הגורר גדול מהערך המקסימלי של כוח החיכוך הסטטי, הגוף יחל בתנועה בכיוון הכוח והחיכוך יהפוך לחיכוך קינטי.

שגיאה ביצירת תמונה ממוזערת:

רגע לפני התנועה - מצב בו הכוח החיצוני המופעל על הגוף שווה בעצמתו לכוח החיכוך המקסימלי (במקרה זה - ההעתק של כוח הכבידה על ציר התנועה המקביל למשטח). אם הכוח החיצוני שפועל על הגוף יגדל במידה כלשהי - הגוף יתחיל לנוע.

חיכוך סטטי (Static friction) הוא כוח החיכוך בין שני גופים שאינם בתנועה זה יחסית לזה. החיכוך הסטטי גורם לגוף להישאר במקומו ומונע את החלקתו על המשטח.

כיוונו של כוח החיכוך הסטטי הוא בניגוד לכיוון של התנועה הפוטנציאלית ובמקביל למשטח.

גודלו של כוח החיכוך הסטטי אינו קבוע, משום שהוא תלוי בגודלו של הכוח החיצוני המופעל על הגוף.

עקרון ההתמד המבוסס על חוקי התנועה של ניוטון, קובע שכאשר שקול הכוחות על גוף שווה לאפס לגוף לא תהיה תאוצה. כלומר: אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum \vec F = 0} אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a}=0} .

כאשר אין תאוצה אין שינוי במהירות. כאשר הגוף נמצא במנוחה המהירות הראשונית שלו היא אפס ואם אין שינוי במהירות כך היא תישאר. כלומר, כל עוד שקול הכוחות הפועל על הגוף הוא אפס הגוף הנח לא יזוז ממקומו. מכך אפשר להסיק גם שאם הגוף לא זז שקול הכוחות הפועלים עליו הוא אפס. לכן אם ידוע שפועל כוח חיצוני על הגוף שגודלו שונה מאפס והגוף אינו זז, ניתן להסיק שכוח החיכוך הסטטי פועל בעצמה שווה ובכיוון מנוגד, כך ש: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F - F_s = 0}

כדי שהגוף יישאר במנוחה כוח החיכוך הסטטי חייב להיות שווה בעצמתו לכוח החיצוני שאליו הוא יתנגד, אחרת סכום הכוחות לא יהיה אפס והגוף יזוז. משום שעל הגוף יכולים לפעול כוחות חיצוניים בעוצמות שונות, גודלו של כוח החיכוך הסטטי אינו קבוע.

$F_{s}\leq \mu _{s}N$

ערכו המקסימלי של כוח החיכוך הסטטי הוא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_s{max} = \mu_s N\,}

כל עוד הכוח החיצוני המופעל על הגוף קטן או שווה לכוח החיכוך הסטטי המקסימלי, הוא לא יוכל לגרום לתנועה והגוף יישאר במקום. במצב זה גודלו של כוח החיכוך הסטטי יהיה שווה לגודלו של הכוח החיצוני. אם הכוח החיצוני יהיה גדול יותר מכוח החיכוך הסטטי המקסימלי, הגוף יתחיל לנוע וכוח החיכוך שיופעל עליו במהלך התנועה יהיה קינטי (ולא סטטי).

כוח החיכוך הסטטי המקסימלי תמיד גבוה יותר מהחיכוך הקינטי. לכך שתי סיבות מכניות. אחת היא שבמהלך תזוזה בחיכוך, כלומר תחת חיכוך קינטי, קיימת שחיקה של החלקים הנוגעים של שני הגופים, מה שהופך אותם לחלקים יותר ומקטין את החיכוך, לעומת חיכוך סטטי, שבו אין שחיקה של הגופים. סיבה שנייה היא שבמהלך חיכוך קינטי אין זמן לכל השקיעות והבליטות בשני הגופים להתאים, כיוון שהגופים יתרחקו אחד מהשני לפעמים בהתאם לשקיעות והבליטות בהם, והכוח שלוחץ אותם לא יקרב אותם לגמרי אחד לשני מיידית אלא אם הוא אינסופי. בזמן שבו הגופים לא לחוצים לגמרי אחד לשני יפעל עליהם פחות חיכוך. בניגוד לכך, בחיכוך סטטי, לשני הגופים כנראה יהיה זמן להתאים את השקיעות והבליטות בהם. זוהי הסיבה לכך שיותר קשה להתחיל להזיז גוף העומד על משטח לא חלק מאשר להמשיך את תנועתו מרגע שהחל בה.

חיכוך בגלגול - חיכוך ללא החלקה וחיכוך עם החלקה

חיכוך גלגול הוא כוח החיכוך בין משטח ובין גוף עגול המתגלגל עליו. ישנם שני סוגי חיכוך בגלגול. חיכוך עם החלקה, וחיכוך ללא החלקה.

חיכוך ללא החלקה אינו מאבד אנרגיה מהמערכת, זהו החיכוך של גלגלי הרכב שלנו כשאנו מאיצים או מאטים בנהיגה רגילה. כאשר האוטו מחליק (למשל בעצירה פתאומית או בשחרור קלאץ' מהיר מדי) אז החיכוך יהיה חיכוך עם החלקה. בחיכוך עם החלקה אובדת אנרגיה.

אפשר להסתכל על הליכתנו כעל גלגול ללא החלקה. גופנו מתקדם, אך המגע בין כף הרגל לרצפה אינו מחליק (ולכן אינו מאבד אנרגיה).

גרר

גרר הוא כוח החיכוך הפועל על גוף הנמצא בתנועה בתוך נוזל או גז. בדרך כלל כוח הגרר פרופורציוני למהירות או למהירות בריבוע, ותלוי בגורמים כמו הצורה של המסה הנעה בזורם, צמיגות הזורם וכדומה.

במקרה הראשון, כוח הגרר פרופורציוני למהירות (תיאור זה מתאים לזורמים בצפיפות מסוימת) הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{f}_d=-\beta\vec{v}} , כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} מהירות הגוף כפונקציה של הזמן, ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} הוא קבוע. במקרה כזה, משוואת התנועה של גוף הנופל נפילה חופשית תחת השפעת כוח החיכוך עם האוויר (חשוב לציין שלעיתים החיכוך עם האוויר פרופורציוני לריבוע המהירות, וזה תלוי בגובה ממנו נזרק הגוף) היא: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle mg-\beta v=ma} . ניתן להציג את המשוואה כמשוואה דיפרנציאלית התלויה במהירות: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta v-m\dot{v}=mg} . ניתן למצוא את פתרון המשוואה בשיטת גורם האינטגרציה, והוא נתון על ידי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\frac{gm}{\beta}+ce^{-\frac{\beta}{m}t}} , כאשר $c$ מתקבל מהצבת תנאי התחלה. כמו כן, על ידי אינטגרציה פעם אחת, נוכל למצוא גם את המיקום של הגוף: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{gm}{\beta}t-\frac{m}{\beta}c_1e^{-\frac{\beta}{m}t}+c_2} כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_2} מתקבלים מהצבת תנאי התחלה.

כוח זה הוא גם אחד הכוחות שעלולים לשבש אוסצילטור הרמוני.

היסטוריה ומחקר

סימולציה של שני משטחים, בעלי פני שטח פרקטליים, המדגימים אינטראקציה היוצרת חיכוך סטטי

תופעות הקשורות בחיכוך ידועות לאנושות עוד מהתקופה הפרהיסטורית, כשאנשים השתמשו בחיכוך כדי להדליק אש, למשל. גם המצרים הקדמונים הכירו בתופעות הקשורות בחיכוך. ישנם ציורי קיר מצריים המראים כיצד משמנים את המסלול לאורכו סוחבים אבנים גדולות ופסלים, וכן נמצאו שרידי שמן על צירי עגלות מצריות.

בעת החדשה, לאונרדו דה וינצ'י ערך ניסויים מדעיים ראשוניים בחיכוך. בשנת 1699 ניסח פיזיקאי צרפתי בשם גיום אמונטון (Guillaume Amontons) את חוקי החיכוך הסטטי כפי שהם ידועים היום, עליהם הוסיף שארל-אוגוסטן דה קולון (Charles-Augustin de Coulomb) את חוקי החיכוך הקינטי בשנת 1785.

ואלו הם חוקי החיכוך כפי שהציגו אותם אמונטון וקולון:

1. כוח החיכוך הקינטי וערכו המרבי של כוח החיכוך הסטטי, שניהם מתכונתיים לכוח הנורמלי F=µN (הכוח הנורמלי הוא הכוח שמשטח אחד מפעיל על השני, בהינתן שיש ביניהם מגע. כוח זה תמיד ניצב למשטח המגע). עם זאת, קבוע הפרופורציה, µ, הנקרא מקדם החיכוך, הוא, ברוב המקרים, שונה. במילים אחרות, על פי רוב, החיכוך הסטטי גדול יותר מאשר הקינטי. הביטוי F=µN מציין ערך מרבי עבור חיכוך סטטי, משום שמתחת לערך זה הגופים אינם נעים זה ביחס לזה, והחיכוך מאזן את הכוח החיצוני הפועל להנעת אחד הגופים ביחס לשני.
2. כוח החיכוך אינו תלוי בשטח או בצורה הגאומטרית של הגופים.
3. כוח החיכוך אינו תלוי באיכות פני השטח של הגופים.
4. כוח החיכוך תלוי בסוגי החומרים מהם עשויים פני השטח של הגופים.
5. כוח החיכוך הקינטי הוא קבוע, וכמעט אינו תלוי במהירות ההחלקה.

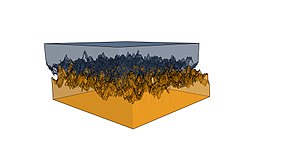
חוקים אלו הם חוקים אמפיריים (כלומר המבוססים ניסיונית) והם מתקיימים באופן כללי עבור מגוון רחב של חומרים. חוקים אמפיריים אלה, אינם מבוססים על עקרונות יסוד, להוציא כמה מקרים יוצאים מן הכלל. כדי להסביר את תופעת החיכוך מתוך עקרונות יסודיים דרוש מודל. במהלך שנות החמישים פותח מודל כזה על ידי פרנק בוודן ודוד טבור (F.P. Bowden and D. Tabor) המסביר את החוקים האמפריים הללו וכן עוד תכונות רבות של כוח החיכוך. על פי המודל שלהם ההתנהגות של כוח החיכוך נובעת מן העובדה שלמשטחים יש חספוס ומן העובדה ששטח המגע בין המשטחים קטן בהרבה מהשטח הגאומטרי שלהם.

במבט מיקרוסקופי, המשטח כבר לא נראה חלק אלא גבשושי. כאשר שני משטחים באים במגע, הבליטות על פני שני המשטחים פוגשות אלו את אלו ראשונות והן נושאות בעומס. שטח המגע האקטיבי הנדרש כדי להחזיק את העומס (הכוח הנורמלי) מורכב מנקודות מגע ספורות בלבד ולפיכך הוא קטן מאד. בנקודות אלו הלחץ הוא עצום (בגלל השטח הקטן) ולכן המשטחים ניתכים אחד לתוך השני בנקודות הללו. העומס מתכונתי לשטח האפקטיבי וגם כוח החיכוך מתכונתי לשטח האפקטיבי. לכן כוח החיכוך מתכונתי לעומס.

דוגמאות נוספות לשימוש בחיכוך

יש פעמים בהם החיכוך הוא גורם נצרך המאפשר את השימוש במכשיר כלשהו, ויש פעמים בהם אנו רוצים להימנע מהחיכוך.

• אמצעי חיכוך שונים בפעילויות של סנפלינג או טיפוס הרים, עוזרים, מאפשרים וגורמים לבטיחות הפעולה. למשל טבעת טיפוס יוצרת חיכוך מאוד גבוה על החבל העובר בתוכה, וזה מה שמאפשר לנו לרדת בבטחה, ובפחות מאמץ.
• החיכוך הרב שיוצרות טביעות אצבע עם החפץ אותו הן באות במגע, מאפשר לנו להחזיק דברים ביתר קלות.
• לעיתים מדביקים על שפתן של מדרגות, פסים המגבירים את החיכוך, ומונעים החלקה.
• אחד הגורמים שאינם מאפשרים קיום של "פרפטום מובילה" הוא החיכוך שגורם לאיבוד אנרגיה בתוך המערכת.
• מגדל בורג' ח'ליפה בדובאי נבנה בשטח חולי, ללא מצע אדמה סלעי או יציב עליו ניתן לבנות ללא תנועת המצע. על כן, נבנו 194 עמודי יסודות עבור הבניין, בעומק של 15 מטרים בלבד. מערך זה של יסודות נסמך על החיכוך הרב שהם יצרו יחד עם החול, ובכך מהווים יסוד יציב למגדל.

ראו גם

• משוואת קולברוק

לקריאה נוספת

• The Friction and Lubrication of Solids / by F.P. Bowden and D. Tabor Oxford : Clarendon Press, 1954
• Sliding friction : physical principles and applications / Bo N.J. PerssonBerlin : Springer, c2000

קישורים חיצוניים

מדיה וקבצים בנושא חיכוך בוויקישיתוף

• כוח החיכוך, באתר המרכז הארצי למורי מוט"ב
• האוניברסיטה העברית, ‏האם דה' וינצ'י טעה?, באתר "הידען", 8 ביולי 2014
• דוגמאות לחיכוך גלגול
• דוגמאות לחיכוך קינטי
• חיכוך, באתר אנציקלופדיה בריטניקה (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

29567003חיכוך