מחומש

מחומש (מְחֻמָּשׁ; בלועזית, מיוונית: פֶּנְטַגוֹן) הוא מצולע בעל חמש צלעות. סכום זוויותיו הפנימיות של מחומש הוא 540 מעלות, ויש בו 5 אלכסונים.
מחומש משוכלל
מחומש משוכלל הוא מחומש שכל צלעותיו שוות זו לזו וכל הזוויות שוות זו לזו. גודל כל אחת מהזוויות הוא 108°. מספר זה אינו מחלק את 360, ולכן לא ניתן לרצף את המישור במחומשים משוכללים.
שטח מחומש משוכלל שאורך צלעו a מחושב על פי הנוסחה:
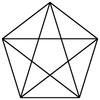
כל אלכסוני המחומש שווים באורכם זה לזה, וכל אחד מקביל לצלע איתה הוא לא חולק קודקוד משותף. אלכסון עם שתי צלעות יוצרים משולש זהב רחב (משולש שווה-שוקיים שהיחס בין הבסיס לשוק הוא יחס הזהב), ואילו שני אלכסונים עם צלע יוצרים משולש זהב צר (שהיחס בין שוק לבסיס הוא יחס הזהב). גם המשולשים הקטנים, שנוצרו בתוך המחומש, הם משולשי זהב. כל האלכסונים יוצרים פנטגרם.
בנייה בסרגל ומחוגה

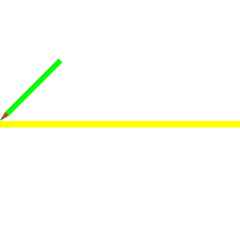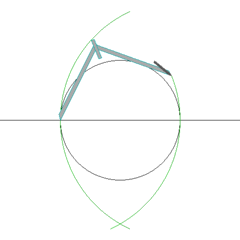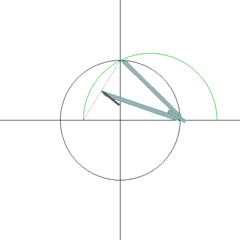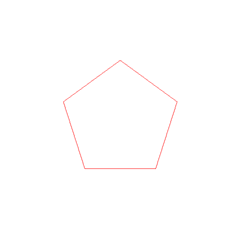
ניתן לבנות מחומש משוכלל על ידי שימוש במחוגה ובסרגל בלבד, על ידי חסימתו במעגל. דרך זו תוארה על ידי אוקלידס בספרו יסודות (ספר רביעי, טענה 11) לפני כאלפיים וארבע מאות שנה. הבניה מבוססת על כך ש- ו- .
אחת הדרכים לכך היא:
- משרטטים מעגל, מרכזו יהיה O (המעגל הירוק שבסרטוט משמאל). נניח שרדיוסו של מעגל זה - יחידה אחת.
- בוחרים על ההיקף נקודה, A, שתהווה אחד מקודקודי המחומש. מעבירים ישר מ-A דרך המרכז, O.
- בונים אנך לקוטר AO, דרך מרכז המעגל, ומסמנים את אחד החיתוכים שלו עם המעגל כ-B.
- מסמנים את הנקודה C במרכז הקטע OB. (המרחק ).
- מעבירים מעגל שמרכזו הנקודה C דרך הנקודה A, מסמנים את נקודת החיתוך בין המעגל לקו OB כ-D. (המרחק , וזהו אורך צלע המחומש החסום במעגל המקורי).
- מעבירים מעגל שמרכזו A דרך הנקודה D; מסמנים את חיתוכיו עם המעגל המקורי (הירוק) באותיות E ו-F.
- מעבירים מעגלים שמרכזם E ו-F דרך הנקודה A, מסמנים את חיתוכיהם עם המעגל המקורי כ-G ו-H בהתאמה.
- הנקודות AEFGH מהוות את קודקודי המחומש המשוכלל.
דרך אחרת מתוארת באנימציה שמשמאל.
תכונות של מחומשים
תכונת פונסלה
כל מחומש חוסם חתך חרוט וחסום בחתך חרוט. מצולע המקיים תכונה זו נקרא מצולע פונסלה (Poncelet).
משפט קלבש
חמשת האלכסונים של מחומש נפגשים בחמש נקודות, ויוצרים כך מחומש פנימי. Clebsch הוכיח (ב-1871) שהמחומש הפנימי דומה פרויקטיבית למחומש המקורי. ב-2007 הראה Schwartz שתכונה זו נכונה לכל מצולע פונסלה בעל מספר אי-זוגי של קודקודים.
שטח
למחומש יש תכונה מעניינת, והיא שניתן לחשב את שטחו ללא טריאנגולציה (ללא חלוקה של שטחו למשולשים), אלא רק על ידי "הליכה מסביבו" וחישוב שטחיהם של משולשים קודקודיים. המתמטיקאי הידוע קרל פרידריך גאוס הוא זה שגילה[1] תכונה זו, ומצא ביטוי המתאר את שטחו של מחומש משטחיהם של משולשים קודקודיים (משולש קודקודי הוא משולש שקודקודיו הם שלושה קודקודים עוקבים של המחומש): אם נסמן ב- את שטח המשולש שקודקודיו הם אז שטח המחומש מקיים את המשוואה הריבועית , כאשר ו- הם הפונקציות הסימטריות הציקליות ממעלה ראשונה ושנייה במשתנים : .
ריצוף של המישור
בין משפחות המצולעים, משפחת המחומשים מציבה בעיות ייחודיות בתחום ריצוף של המישור. המתמטיקאית דוריס שאטשניידר חקרה מהו סימן ההיכר של מחומשים שניתן ליצור מהם ריצוף לעומת אלו שלא. היא אפיינה מספר מחומשים רלוונטיים, אך בעיית המחומשים בכללותה נותרה עדין לא פתורה, וייתכן וקיימים מחומשים נוספים הניתנים לשימוש במישור וטרם התגלו. כיום ידועים 13 דפוסים של מחומשים זהים שמאפשרים ריצוף מלא של המישור ללא חללים, בדומה לפסיפס או כוורת דבורים. המתמטיקאית החובבת מרג'ורי רייס גלתה ארבעה מהם.
קישורים חיצוניים
הערות שוליים
| מצולעים ופאונים | ||
|---|---|---|
| מושגים | מצולע • פאון • קודקוד • צלע • מקצוע • פאה • זווית חיצונית • אלכסון | |
| מצולעים | ||
| לפי מספר צלעות | משולש • מרובע • מחומש • משושה • משובע • מתומן | |
| משולשים | משולש ישר-זווית • משולש שווה-שוקיים • משולש שווה-צלעות | |
| מרובעים | מקבילית • טרפז • טרפז שווה-שוקיים • מרובע ציקלי • דלתון • דלתון ריצוף • מעוין • מלבן • ריבוע | |
| כוכבים | פנטגרם • מגן דוד • אניאגרם | |
| תכונות | מצולע משוכלל • מצולע שווה-צלעות • מצולע קמור • כוכב | |
| פאונים | ||
| פאונים משוכללים | ארבעון • קובייה • תמניון • תריסרון • עשרימון | |
| פאונים ארכימדיים | ארבעון קטום • קובוקטהדרון • קובייה קטומה • תמניון קטום • רומביקובוקטהדרון • קובוקטהדרון קטום • קובייה מסותתת • איקוסידודקהדרון • דודקהדרון קטום • איקוסהדרון קטום • רומביקוסידודקהדרון • איקוסידודקהדרון קטום • דודקהדרון מסותת | |
| פאונים אחרים | פירמידה • מנסרה • אנטי-מנסרה • מקבילון • מעוינון • תיבה • איקוסיטטרהדרון | |
| תכונות | פאון משוכלל • פאון משוכלל למחצה • פאון ארכימדי | |
| הכללות | ||
| הכללות | סימפלקס • היפרקובייה • טסרקט | |
מחומש39455812Q127840


