שכבת גבול

תרשים של שכבת גבול, המציג את המעבר משכבה למינרית לתנאים טורבלנטים

שכבת גבול בפיזיקה ובמכניקת זורמים היא שכבת זורם הנמצאת בקרבה למשטח בה צמיגות הזורם משמעותית. הצמיגות מקטינה את התכונה (מהירות / ריכוז/ טמפרטורה) המקומית של הזורם (עד כדי עצירה) ואחראית ליצור החיכוך (מאמצי גזירה) במשטח.

שכבת הגבול בכנף של כלי טיס היא חלק מהזרימה הצמודה לכנף. באטמוספירת כדור הארץ, "שכבת הגבול האטמוספירית" היא שכבת האוויר הקרובה לקרקע המושפעת מחום, לחות או ממומנטום המועבר אל הקרקע או מהקרקע.

יש שני סוגי שכבות גבול של זרימה:

• שכבת גבול למינרית - בתוכה הזרימה חלקה ושכבתית ללא מערבולות. עקב חיכוך הזרימה הלמינרית יוצרת פחות גרר לעומת הזרימה הטורבלנטית, אך היא פחות יציבה. בזרימה על גבי משטח כנף שכבת הגבול מתחילה כלמינרית, וככל שמתקדמת לאורך הכנף עובייה הולך וגדל. שכבת גבול למינרית נוטה יותר להתנתק באופן פתאומי מאשר זרימה טורבלנטית, דוגמה אינטואיטיבית: לזרימה הלמינרית מומנטום גדול יותר להמשיך בתנועתה לעומת הזרימה הטורבולנטית אשר לוקחת אנרגיה משכבות עליונות ומעבירה לשכבות זרימה תחתונות, ניתן לדמיין זאת כאופנוען המגיע במהירות גדולה לרמפה, מאחר שקיים מומנטום גדול האופנוע יתנתק מהמשטח לעומת המקרה בו לאופנוען קיימת אותה כמות אנרגיה אך זו לא מסודרת ולכן עם הגיעו לרמפה הוא יתרומם מעט ויחזור יותר מהר למשטח מאחר שהמומנטום שלו לא בכיוון אחד.

• שכבת גבול טורבולנטית - במרחק מסוים מתחילת המשטח, הזרימה הלמינרית החלקה מתחילה להתפרק (כוחות הצמיגות לא מתגברים על כוחות האינרציה עקב הפרעות בזרימה). לאחר אזור "מעבר" הופכת לזרימה טורבלנטית. קיימים חלקי מכונות שבהם גורמים לזרימה טורבולנטית על מנת לדחות את הניתוקים בזרימה.

ישנן שכבות גבול המפורסמות הנסיבות שבגללן הן נוצרו. לדוגמה: שכבת גבול סטוקס - שכבת הגזירה הדקה המתפתחת בגופים תונדים, שכבת גבול בלזיוס - מתייחסת לפתרון הדמיות של זרימה מציפה אחידה הזורמת על פני משטח ישר, שכבת גבול אקמן - מתקבלת כאשר זורם מסתובב וכוחות הצמיגות מתאזנים על ידי אפקט קוריוליס (ולא על ידי כוחות אינרציה). שכבת גבול תרמית המתפתחת כתוצאה ממעבר חום.

רקע

לודוויק פרנטל

משוואת הגבול האווירודינמיות הוגדרו לראשונה על ידי לודוויק פרנטל במאמר שהוצג בקיץ 1904 בקונגרס העולמי השלישי למתמטיקאים בהיידלברג שבגרמניה. המודל של לודוויק מפשט את משוואות הזרימה של הנוזל על ידי פיצול שדה הזרימה לשני תחומים. האחד בתוך שכבת הגבול בו האיבר הדומיננטי הוא הצמיגות, הגורם העיקרי ליצירת כוח גרר חיכוך (skin friction) הפועל על הגוף. התחום השני הוא מחוץ לשכבת הגבול בו ניתן להזניח את איבר הצמיגות במשוואה, והזנחה זאת לא פוגעת בפתרון המשוואה. גישה זו נותנת פתרון אנליטי לזרימה בשני התחומים, פישוט משמעותי למשוואות נאוויה-סטוקס. החלק הגדול של מעבר החום מגוף לסביבה ולהפך קורה גם הוא בתוך שכבת הגבול. גרדיאנט הלחץ לאורך שכבת הגבול בכיוון נורמל למשטח נשמר קבוע לאורך שכבת הגבול והוא זהה על המשטח עצמו. עובי של שכבת הגבול מוגדרת כמרחק מהגוף המוצק עד למקום שבו המהירות של הזרימה הצמיגה שווה בערכה ל־99% ממהירות של הזרימה החופשית. הגדרה נוספת לעובי שכבת הגבול, מתייחסת לשטף מעבר מסה. במקרה זה עובי שכבת הגבול הוא העובי אשר ייתן מעבר מסה זהה בין שני המקרים הבאים. האחד, החלקה על הגוף וזורם לא צמיג אל מול המצב השני, זורם צמיג ואי-החלקה על הגוף. מצב אי-החלקה משמעותו שמהירות הזורם בשטח המגע על הגוף היא אפס ביחס למהירות הגוף, וטמפרטורת הזורם שווה לטמפרטורת המשטח של הגוף.

משוואת שכבת הגבול

תמונה מספר 2, פרופיל מהירות של שכבת גבול למינרית

משוואת שכבת הגבול עבור המקרה של זרימה מציפה מעל לפלטה שטוחה וחצי אינסופית. במקרה זה ניתן להשתמש בהנחות המפשטות את הבעיה והן:

• נוזל ניוטוני
• נוזל בלתי דחיס
• בעיה דו־ממדית
• בעיה ללא כוחות גוף

נפתח את משוואות נאוויה-סטוקס ומשוואת שימור המסה :

$\frac{\partial u}{\partial x}+\frac{\partial \upsilon }{\partial y}=0$

$u\frac{\partial u}{\partial x}+\upsilon \frac{\partial u}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\nu (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2})$

$u\frac{\partial \upsilon }{\partial x}+\upsilon \frac{\partial \upsilon }{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+\nu (\frac{{\partial }^2\upsilon }{\partial x^2}+\frac{{\partial }^2\upsilon }{\partial y^2})$

נעזר באנליזת סדרי גודל. נגדיר משתנים מנורמלים.

$U=u/u^{*}$

$V=v/v^{*}$

$P=p/p^{*}$

$X=x/l$

$l$ אורך אופייני

$Y=y/\delta$

$\delta$ עובי אופייני של שכבת הגבול

$T=t/(l/u^{*})$

שכבת הגבול דקה ולכן ניתן לרשום:

$ϵ=\frac{\delta }{l}<<1$

נציב למשוואת שימור המסה ונקבל:

${\displaystyle }$

$=0$ $\frac{v^{*}\partial (V)}{\delta \partial (Y)}$ $+$ $\frac{u^{*}\partial (U)}{l\partial (X))}$ $=$ $\frac{v^{*}\partial (v/v^{*})}{\delta \partial (y/\delta )}$ $+$ $\frac{u^{*}\partial (u/u^{*})}{l\partial (x/l)}$ $\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=$

${\displaystyle }$

$\frac{\partial (V)}{\partial (Y)}\approx o(1)$ $\frac{\partial (U)}{\partial (X)}\approx$

${\displaystyle }$

נקבל

${\displaystyle }$

$\frac{v^{*}}{u^{*}}=\frac{\delta }{l}=ϵ<<1$

נירמול משוואת שימור המומנטום בכיוון ציר $\hat{x}:$

${\displaystyle }$

$)$ $+\frac{{\partial }^{2}U}{\partial Y^2}$ $\frac{{\partial }^{2}U}{\partial X^2}$ ${ϵ}^2$ $($ $+\frac{\mu u^{*}}{{\delta }^2}$ $\frac{\partial P}{\partial X}$ $-\frac{p^{*}}{l}$ $=$ $)$ $+V\frac{\partial U}{\partial Y}$ $+U\frac{\partial U}{\partial X}$ $\frac{\partial U}{\partial T}$ $($ $\frac{\rho (u^{*}{)}^2}{l}$

${\displaystyle }$

$=\sqrt{l^2\frac{\mu }{\rho u^{*}l}}$ $\sqrt{\frac{\mu u^{*}l}{\rho (u^{*}{)}^2}}$ $\delta =$ $\Rightarrow$ $=\frac{\mu u^{*}}{{\delta }^2}$ $$ $\frac{\rho (u^{*}{)}^2}{l}$ $\Rightarrow$

${\displaystyle }$

$=\sqrt{\frac{1}{Re}}$ $=\sqrt{\frac{\mu }{\rho u^{*}l}}$ $=\frac{\delta }{l}$ $ϵ$

${\displaystyle }$

$=\rho (u^{*}{)}^2$ $p^{*}$ $\Rightarrow$ $\frac{\rho (u^{*}{)}^2}{l}$ $\sim$ $\frac{p^{*}}{l}$

${\displaystyle }$

$+\frac{{\partial }^{2}U}{\partial Y^2}$ $\frac{{\partial }^{2}U}{\partial X^2}$ $+\frac{1}{Re}$ $\frac{\partial P}{\partial X}$ $-$ $=$ $+V\frac{\partial U}{\partial Y}$ $+U\frac{\partial U}{\partial X}$ $\frac{\partial U}{\partial T}$ $\hat{x}:$

${\displaystyle }$

$)$ $+\frac{{\partial }^{2}V}{\partial Y^2}$ $\frac{{\partial }^{2}V}{\partial X^2}$ $($ $+\frac{1}{R{e}^2}$ $\frac{\partial P}{\partial Y}$ $-$ $=$ $)$ $+V\frac{\partial v}{\partial Y}$ $+U\frac{\partial v}{\partial X}$ $\frac{\partial V}{\partial T}$ $($ $\frac{1}{Re}$ $\hat{y}:$

מאחר ש $Re>>1$ נקבל את משוואת שכבת הגבול המנורמלות:

משוואות הגבול המנורמלות

${\displaystyle }$

$+\frac{{\partial }^{2}U}{\partial Y^2}$ $\frac{\partial P}{\partial X}$ $-$ $=$ $+V\frac{\partial U}{\partial Y}$ $+U\frac{\partial U}{\partial X}$ $\frac{\partial U}{\partial T}$

${\displaystyle }$

$0$ $=$ $\frac{\partial P}{\partial Y}$

${\displaystyle }$

$0$ $=$ $+\frac{\partial V}{\partial Y}$ $\frac{\partial U}{\partial X}$

${\displaystyle }$

משוואות הגבול הממדיות

${\displaystyle }$

$\frac{{\partial }^{2}u}{\partial y^2}$ $+\frac{\mu }{\rho }$ $\frac{\partial p}{\partial x}$ $\frac{\partial 1}{\partial \rho }$ $-$ $=$ $+v\frac{\partial u}{\partial y}$ $+u\frac{\partial u}{\partial x}$ $\frac{\partial u}{\partial t}$

${\displaystyle }$

${\displaystyle }$

$0$ $=$ $\frac{\partial p}{\partial y}$

${\displaystyle }$

$0$ $=$ $+\frac{\partial v}{\partial y}$ $\frac{\partial u}{\partial x}$

${\displaystyle }$

הלחץ נקבע מהבעיה הפוטנציאלית.

סכימה לאנליזה /נומריקה של חיבור הבעיה החיצונית (זרימה פוטנציאלית) לבעיה הפנימית (זרימה צמיגה)

זרימה מחוץ לשכבת הגבול:

${\displaystyle }$

$+viscosity$ $\frac{\partial p}{\partial x}$ $-$ $=$ $)$ $+v_0\frac{\partial u_0}{\partial y}$ $+u_0\frac{\partial u_0}{\partial x}$ $\frac{\partial u_0}{\partial t}$ $($ $\rho$

באיבר הימיני ה-viscosity מתבטל מחוץ לשכבת הגבול

${\displaystyle }$

ו-$v_0\frac{\partial u_0}{\partial y}$ גם הוא מתבטל מתנאי אי-חדירה

זרימה בשכבת הגבול:

${\displaystyle }$

$\frac{{\partial }^{2}u}{\partial y^2}$ $\mu$ $+$ $\frac{\partial p}{\partial x}$ $-$ $=$ $)$ $+v\frac{\partial u}{\partial y}$ $+u\frac{\partial u}{\partial x}$ $\frac{\partial u}{\partial t}$ $($ $\rho$

${\displaystyle }$

$0$ $=$ $\frac{\partial p}{\partial y}$

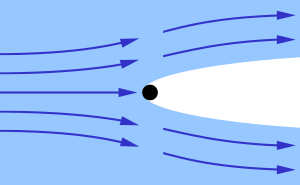
לאורך הקן של שכבת הגבול, הקן המקווקו בתמונה מספר 2, גרדיאנט הלחץ שווה מרציפות, נקבל:

${\displaystyle }$

$\frac{{\partial }^{2}u}{\partial y^2}$ $+\mu$ $u_0\frac{\partial u_0}{\partial x}$ $+\rho$ $\frac{\partial u_0}{\partial t}$ $\rho$ $=$ $)$ $+v\frac{\partial u}{\partial y}$ $+u\frac{\partial u}{\partial x}$ $\frac{\partial u}{\partial t}$ $($ $\rho$

עובי שכבת הגבול

עובי שכבת הגבול הוא הגובה מעל למשטח עליו מתפתחת שכבת גבול בו מתקיים תנאי אי החדירה בעבור הזרימה שמחוץ לשכבת הגבול. נהוג לסמן עובי זה באות $\delta$. עובי זה מוגדר כנקודה בה המהירות מגיעה לכדי 99% מהמהירות של הזרימה החיצונית. בעבור זרימה קבועה מעל לפלטה שטוחה מתקבל:

$u\left(y\right)=0.99u_0$

הפיזיקאי הגרמני בלזיוס (Paul Richard Heinrich Blasius ) פתר את משוואות שכבת הגבול בעזרת דמיות תוך הגדרת משתנה חסר מימד: $\eta =\frac{y}{\delta \left(x\right)}=y{\left(\frac{u_0}{\nu x}\right)}^{1/2}$. שבעזרתו הוא קיבל פתרון בעבור עובי שכבת הגבול:

$\delta \approx 4.91\sqrt{\frac{\nu x}{u_0}}$

משוואת שכבת הגבול האינטגרלית

את משוואת שכבת הגבול הקושרת את הזרימה החיצונית אל הפנימית ניתן לפתור באופן הבא:

נבצע אינטגרציה על המשוואה ונקבל:

$\frac{1}{2}\frac{\partial }{\partial x}\underset{0}{\overset{\mathrm{\infty }}{\int }}{u}^{2}dy+\underset{0}{\overset{\mathrm{\infty }}{\int }}v\frac{\partial u}{\partial y}dy-\underset{0}{\overset{\mathrm{\infty }}{\int }}{u}_0\frac{\partial u_0}{\partial x}dy=\nu \left({\frac{\partial u}{\partial y}|}_0^{\mathrm{\infty }}\right)$

נבצע אינטגרציה על משוואת שימור המסה ונקבל:

$v\left(y\right)-v\left(0\right)=-\underset{0}{\overset{y}{\int }}\frac{\partial u}{\partial x}dy$

מכאן נציב את $v\left(y\right)$ שקיבלנו את תוך משוואת שכבת הגבול ונקבל:

$\frac{1}{2}\frac{\partial }{\partial x}\underset{0}{\overset{\mathrm{\infty }}{\int }}{u}^{2}dy+v\left(0\right)\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\partial u}{\partial y}dy-\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\partial u}{\partial y}\left(\underset{0}{\overset{y}{\int }}\frac{\partial u}{\partial x}dy\right)dy-\underset{0}{\overset{\mathrm{\infty }}{\int }}{u}_0\frac{\partial u_0}{\partial x}dy=-\frac{{\tau }_w}{\rho }$

לאחר פתרון נקבל את משוואת שכבת הגבול האינטגרלית:

$\frac{\partial }{\partial x}\left[{u_0}^2\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{u}{u_0}(1-\frac{u}{u_0})dy\right]+u_0\frac{\partial u_0}{\partial x}\underset{0}{\overset{\mathrm{\infty }}{\int }}(1-\frac{u}{u_0})dy-v\left(0\right)u_0=\frac{{\tau }_w}{\rho }$

ניתן כעת להגדיר מספר גדלים אופייניים לשכבת הגבול:

עובי הזזה- גודל הספיקה של הפתרון לזרימה החיצונית אשר יעלם עקב שכבת הגבול.

${\delta }_1=\underset{0}{\overset{\mathrm{\infty }}{\int }}(1-\frac{u}{u_0})dy$

עובי מומנטום- גודל המומנטום של הפתרון לזרימה החיצונית אשר יעלם עקב שכבת הגבול.

${\delta }_2=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{u}{u_0}(1-\frac{u}{u_0})dy$

עובי אנרגיה- כמות האנרגיה אשר אובדת מהפתרון של הזרימה החיצונית עקב שכבת הגבול.

${\delta }_3=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{u}{u_0}(1-{\left(\frac{u}{u_0}\right)}^2)dy$

וכעת המשוואה לתראה כך:

$\frac{\partial }{\partial x}\left({u_0}^2{\delta }_2\right)+u_0\frac{\partial u_0}{\partial x}{\delta }_1=\frac{{\tau }_w}{\rho }+u_{0}v\left(0\right)$

שכבת גבול תרמית

שכבת גבול תרמית מתפתחת במידה וקיים שוני בין טמפרטורת הזורם לבין המשטח עליו הוא זורם. בקצה השמאלי של הפלטה בתמונה מספר 2, ב-0=x, פרופיל הטמפרטורה אחיד

${\displaystyle }$

$T(y)=T_0$

חלקיקי הזורם אשר באים במגע עם המשטח מגיעים לשיווי משקל תרמי, ומכך לאותה טמפרטורה, חלקיקים אילו מחליפים אנרגיה עם שכבת הזורם הנמצאת מעליהם וכתוצאה מתפתח גרדיאנט טמפטורה בזורם. התחום בו קיים גרדיאנט טמפרטורה הוא שכבת הגבול התרמית, עובי זה ${\delta }_t$ מוגדר כאשר הערך של $y$ נותן את היחס הבא: $=0.99$ $\frac{T_s-T}{T_s-T_0}$ עם התרחקות מהקצה השמאלי של הפלטה, ההשפעה של מעבר החום גדלה וחודרת עמוק יותר לתוך הזרימה החופשית ושכבת הגבול התרמית גדלה. על ידי שימוש בחוק פורייה נקבל את שטף החום מהמשטח אל הזורם

${\displaystyle }$

${}_0$ ${}_{=}$ ${}_y$ $\mid$ $\frac{\partial T}{\partial y}$ $-k_f$ $=$ $q^{\prime }{\text{'}}_s$

במשטח, ב-$y=0$ לא קיימת תנועת נוזל ומעבר אנרגיה מתבצע על ידי מנגנון ההולכה. על ידי הוספת חוק ניוטון לקירור

${\displaystyle }$

$h(T_s-T_0)$ $=$ $q^{\prime }{\text{'}}_s$

והשוואת שטף החום נקבל את מקדם הסעת החום

${\displaystyle }$

$\frac{1}{T_s-T_0}$ $)$ ${}_0$ ${}_{=}$ ${}_y$ $\mid$ $\frac{\partial T}{\partial y}$ $-k_f$ $($ $=$ $h$

בנוסחה האחרונה ניתן לראות כי למצב בשכבת הגבול התרמית יש השפעה גדולה על גרדיאנט הטמפרטורה, וזה משפיע על קצב מעבר החום לאורך שכבת הגבול התרמית. מאחר שהערך-$T_s-T_0$ קבוע, בלתי תלוי ב-$x$

${\displaystyle }$

ו-${\delta }_t$ גדלה עם עליית הערך של $x$

ו-גרדיאנט הטמפרטורה נחלש עם עליית הערך של $x$

${\displaystyle }$

נובע מכך ששטף החום ומקדם הסעת החום בהסעה קטנים גם הם עם עליית הערך של $x$

שכבת גבול של הריכוז

אוויר הזורם מעל בריכת מים, יגרום לחלק מהנוזל להתאדות, אדי מים אילו יכנסו לזרימת האוויר. זוהי דוגמה למעבר של חומר A לחומר B. שכבת הגבול של הריכוז היא התחום בו קיים בזורם גרדיאנטים של ריכוז. עובי שכבת הגבול ${\delta }_c$ מוגדר על ידי

${\displaystyle }$

$=0.99$ $\frac{C_{As}-C_A}{C_{As}-C_{A0}}$

${\displaystyle }$

ריכוז מולרי של חומר A במשטח $C_{As}$

${\displaystyle }$

ריכוז מולרי של חומר A זורם $C_{A0}$

עם ההתרחקות מהקצה השמאלי בתמונה מספר 2, 0=x, אפקט מעבר הריכוז מתחזק ונכנס אל שכבות יותר עמוקות בזרימה ושכבת הגבול של הריכוז גדלה.

דוגמאות

אובייקט (בשחור) נמצא בזרימת נוזל שמהירותו גבוהה, לחץ הנוזל אחרי האובייקט נמוך מהלחץ הקריטי של הנוזל וכתוצאה נוצרת בועת אד המכילה את האובייקט.

טיל טורפדו מדגם VA-111 Shkval נע במים במהירות של כ-370 קמ"ש (100 מטר לשנייה) על ידי שימוש בעיקרון ה-קוויטציה, כך שהוא נע בבועת גז הנוצרת על ידי חרטום הטיל יחד עם גזים מהמנוע. כתוצאה משתנה הזורם (שקודם לכן היה מים) בשכבת הגבול, וכוח הגרר יורד משמעותית ומאפשר לטיל הטורפדו לנוע במהירות מאוד גבוהה במים.

ראו גם

• מספר ריינולדס
• תנאי גבול בדינמיקה של זורמים
• צמיגות
• זרימה טורבולנטית

לקריאה נוספת

• Schlichting, H. (1979). Boundary-Layer Theory (7 ed.). New York (USA): McGraw-Hill

• ׁINCROPERA. . FUNDAMENTALS OF HEAT AND MASS TRANSFER (7 ed.).

קישורים חיצוניים

מדיה וקבצים בנושא שכבת גבול בוויקישיתוף

• שכבת גבול, באתר אנציקלופדיה בריטניקה (באנגלית)

• THE NATIONAL COMMITTEE FOR FLUID MECHANICS FILMS, סרטון באתר יוטיוב

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

שכבת גבול40490205Q752193