שיטת החצייה
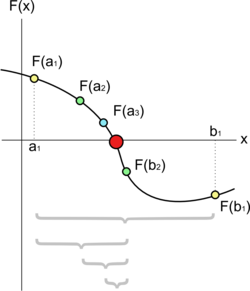

באנליזה נומרית, שיטת החצייה (באנגלית: bisection method) היא אלגוריתם למציאת שורש של פונקציה, אשר עושה שימוש איטרטיבי בחלוקת המרווח לשורש בשניים וכך לבחור מרווח קטן יותר שבו השורש נמצא. תהליך זה נמשך עד שהפער מספיק קטן.
תיאור
נניח שאנו רוצים לפתור את המשוואה , כאשר היא פונקציה רציפה. בהינתן שתי נקודות ו-, שלערכי הפונקציה בהן יש סימנים הפוכים, ממשפט ערך הביניים נובע שלפונקציה יש לפחות שורש אחד במרווח זה . שיטה זו מחלקת את המרווח בשתיים בכל איטרציה:
אחר כך, ישנן שלוש אפשרויות: באפשרות הראשונה ובכך מצאנו את מבוקשנו. שתי האפשרויות האחרות הן של- ול- יש ערכים הפוכים בסימנם, או של- ול- יש ערכים הפוכים בסימנם. האלגוריתם ימשיך לאיטרציה הבאה למרווח בין שני הערכים, שבהם הסימנים של הפונקציות שלהם הפוכים.
אם היא פונקציה רציפה במרווח ו-, אזי שיטת החצייה מתכנסת. למעשה, ניתן לחשב שגיאה מוחלטת לשיטה החצייה ברוב המקרים:
לאחר צעדים. במילים אחרות, השגיאה מתחלקת בשתיים בכל איטרציה, לכן השיטה מתכנסת באופן ליניארי (סדר ההתכנסות הוא 1). אבל השיטה מתכנסת באופן ודאי אם ל- ול- יש ערכים הופכיים. מכאן, שיטת החצייה יעילה פחות משיטת ניוטון-רפסון (מתכנסת לאט יותר), אולם בניגוד לשיטת ניוטון-רפסון, ההתכנסות בה מובטחת.
פסאדו-קוד
להלן הצגה של שיטה החצייה בקוד פייתון. הערכים ההתחלתיים של
ו-
חייבים להיות כך ש-
(כמו שנדרש למעלה). המשתנה epsilon מגדיר כמה מדויקת תהיה התוצאה.
# שיטת החצייה
while (b - a) > epsilon:
#חישוב הערך האמצעי
c = (a + b) / 2.
if f(a)*f(c) > 0:
#התעלם מהחצי השמאלי
a = c
else:
#התעלם מהחצי הימני
b = c
קישורים חיצוניים
- שיטת החצייה ב-MathCad.
- שיטת החצייה, באתר MathWorld (באנגלית)
שיטת החצייה37988536Q866300


