בעיית אוסף הקופונים

מספר הקופונים (בציר האנכי) כנגד מספר הדגימות הנדרש בתוחלת (בציר האופקי)

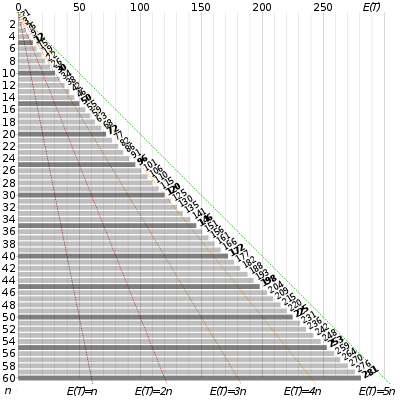
בתורת ההסתברות, בעיית אוסף הקופונים היא בעיה קלאסית הדנה במשחק שבו נאספים קופונים מתוך תיבה עם n קופונים שונים, בהסתברות שווה עם החזרה, והמטרה היא לאסוף את כל הקופונים. מהי ההסתברות שנדרשים לפחות t דגימות כדי לצפות בכל n הקופונים לפחות פעם אחת? ניתוח מתמטי מראה שתוחלת מספר הדגימות הנדרש כדי לצפות בכל קופון לפחות פעם אחת גדלה כתלות ב-n לפי $\Theta (n\log(n))$ (לדוגמה כאשר מספר הקופונים הוא n = 50, נדרשות כ-225 דגימות).

עיקרון חשוב להבנת הבעיה הוא שנדרש מספר דגימות מועט מאד כדי לאסוף את הקופונים הראשונים, ואילו כדי לצפות בקופונים האחרונים (אלו שלא נצפו קודם לאחר שכמעט כל הקופונים נצפו) נדרש מספר גדול של דגימות. למשל כאשר יש 50 קופונים ו-49 מהם כבר נצפו, ידרשו בממוצע כ-50 דגימות כדי לצפות בקופון האחרון.

פתרון הבעיה

נסמן T כזמן הנדרש (או מספר הדגימות) לאיסוף n קופונים, נסמן ב$t_{i}$ את הזמן הנדרש לאיסוף הקופון ה-i לאחר שנאספו i-1 קופונים. נתייחס אל T ו-$t_{i}$ כאל משתנים מקריים. נשים לב שההסתברות לאיסוף קופון חדש (לא אחד מתוך ה-i-1 שכבר נצפו) היא $p_{i}={\frac {n-(i-1)}{n}}$. הזמן הנדרש לאיסוף הקופון ה-i ($t_{i}$) מתפלג לפי התפלגות גאומטרית עם תוחלת של ${\frac {1}{p_{i}}}$. באמצעות לינאריות התוחלת ניתן לשערך את התוחלת לאיסוף כל הקופונים:

$${\begin{aligned}\operatorname {E} (T)&=\operatorname {E} (\sum _{i=1}^{n}t_{i})=\operatorname {E} (t_{1})+\operatorname {E} (t_{2})+\cdots +\operatorname {E} (t_{n})={\frac {1}{p_{1}}}+{\frac {1}{p_{2}}}+\cdots +{\frac {1}{p_{n}}}\\&={\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{1}}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n}}\right)\,=\,n\cdot H_{n}.\end{aligned}}$$

כאשר $H_{n}$ הוא המספר ההרמוני ה-n. בניתוח אסימפטוטי מקבלים שכאשר $n\to \infty$:

$\operatorname {E} (T)=n\cdot H_{n}=n\log n+\gamma n+{\frac {1}{2}}+o(1)$

כאשר $\gamma \approx 0.5772156649$ הוא קבוע אוילר-מסקרוני. באמצעות אי-שוויון מרקוב ניתן לחסום את ההסתברות שהזמן הנדרש לאיסוף כל הקלפים יעלה על $\ c\,nH_{n}$:

$\operatorname {P} (T\geq c\,nH_{n})\leq {\frac {1}{c}}.$

חישוב השונות

ניתן לקבל חסם למספר התצפיות הנדרש לפי השונות. תוך שימוש בכך שהמשתנים המקרים $t_{i}$ בלתי תלויים:

$${\begin{aligned}\operatorname {Var} (T)&=\operatorname {Var} (t_{1})+\operatorname {Var} (t_{2})+\cdots +\operatorname {Var} (t_{n})\\&={\frac {1-p_{1}}{p_{1}^{2}}}+{\frac {1-p_{2}}{p_{2}^{2}}}+\cdots +{\frac {1-p_{n}}{p_{n}^{2}}}\\&=\left({\frac {n^{2}}{n^{2}}}+{\frac {n^{2}}{(n-1)^{2}}}+\cdots +{\frac {n^{2}}{1^{2}}}\right)-\left({\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{1}}\right)\\&=n^{2}\cdot \left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)-n\cdot H_{n}\\&=n^{2}\cdot \left({\frac {\pi ^{2}}{6}}-{\frac {1}{n}}+{\frac {1}{2n^{2}}}\right)-\left(n\log n+\gamma n+{\frac {1}{2}}\right)+o(1)\\&<{\frac {\pi ^{2}}{6}}n^{2}.\end{aligned}}$$

כאשר $\pi ^{2}/6$ הוא ערך של פונקציית זטא של רימן. (ראו בעיית בזל). באמצעות אי-שוויון צ'בישב מתקבל החסם:

$\operatorname {P} \left(|T-nH_{n}|\geq c\,n\right)\leq {\frac {\pi ^{2}}{6c^{2}}}.$