לדלג לתוכן

מקטב

מתוך המכלול, האנציקלופדיה היהודית
הדגמת פעולתו של של מקטב שמסנן את האור המקוטב חלקית המוחזר מפני שלולית. משמאל: צילום בו הענן שנראה בהחזרה מפני המים מפריע לצילום הקרקעית. מימין: צילום בשימוש במקטב המכוון כדי לצמצם את ההחזרה ולאפשר תמונה ברורה של הקרקעית דרך פני המים.
במחצית העליונה של התמונה: מסנן מקטב מצמצם את ההחזרה ממראת הרכב ומאפשר לראות את הצלם דרך זכוכית החלון. ההחזרות מהחלון האחורי של המכונית אינן מסוננות כיוון שכפי שחוזות משוואות פרנל, הן פחות מקוטבות. במחצית התמונה התחתונה: צילום ללא מקטב מדגים את ההחזרה המתקבלת מהמראה ללא התערבות.

מְקַטֵּב (בלועזית: פולרייזר) הוא מסנן המאפשר לגלים אלקטרומגנטיים בעלי קיטוב מסוים לעבור דרכו תוך שהוא מונע מגלים בעלי קיטובים אחרים לעבור.[1] מקטבים משמשים בטכניקות ובמכשירים אופטיים רבים. השימוש במקטבים נפוץ בצילום ובטכנולוגיית גבישים נוזליים (LCD). כפי שרואים בתמונות משמאל, ניתן להשתמש במקטב המורכב על מצלמה כדי לסנן החזרות לא רצויות. מקטבים נמצאים בשימוש נפוץ גם עבור סוגים אחרים של גלים אלקטרומגנטיים מלבד אור נראה, כגון גלי רדיו, גלי מיקרו וקרני רנטגן.

במציאות, מקטבים אינם חוסמים באופן מושלם את הקיטוב הניצב לציר הקיטוב שלהם; היחס בין העברת הרכיב הלא רצוי להעברת הרכיב הרצוי נקרא "יחס הכחדה", כאשר ערכים גבוהים יותר מיצגים ביצועים טובים יותר, דהיינו הנחתה גבוהה יותר של רכיב הקיטוב הבלתי רצוי. ערכים אופייניים הם בין כ-1:500 או 1:1000 עבור פולארויד לכ- 1:1,000,000 עבור פריזמת גלן-טיילור.[1][2]

כל מנגנוני הקיטוב (בליעה סלקטיבית, החזרה, פיזור ושבירה כפולה) מבוססים על צורה כלשהי של חוסר סימטריה, הנחוצה כדי להעדיף קיטוב מסוים.[3] חוסר הסימטריה יכול להיות מינורי, כמו שוני בזווית הפגיעה, אבל בדרך כלל הוא קשור באנאיזוטרופיות ברורה בחומר עצמו.[3]

סוגי המקטבים העיקריים הם מקטבים קוויים ומקטבים מעגליים.

מקטבים קוויים

מקובל כי אם מתייחסים ל"מקטב", ללא תיאור הכיווניות שלו, הכוונה היא למקטב קווי.[1]

ניתן לחלק מקטבים קוויים לשתי קטגוריות כלליות: מקטבים בולעים הנקראים גם מקטבים דיכרואים, שבהם מצבי הקיטוב הלא רצויים נבלעים על ידי ההתקן, ומקטבים מפצלי קרניים, שבהם הקרן הלא מקוטבת מפוצלת לשתי קרניים עם מצבי קיטוב ניצבים.

חוק מאלוס

ערך מורחב – חוק מאלוס

כאשר מקטב קווי אידיאלי ממוקם בקרן אור מקוטבת ליניארית, עוצמת הקרינה (I) של האור שעובר דרכו ניתנת על ידי I=I0cos2θi

כאשר I0 היא העוצמה ההתחלתית ו-θi היא הזווית בין כיוון הקיטוב ההתחלתי של האור לציר המקטב.[4][5]

הדרך למדוד אם התקן כלשהו הוא אכן מקטב קווי היא בדיקה האם הוא מציית לחוק מאלוס: כאשר ממקמים מקטב נוסף, המכונה אנאליזר, אחרי המקטב הנבדק, לפי חוק מאלוס יתקבל מקסימום העברה כאשר הזווית בניהם היא אפס, ומינימום כאשר הזווית בניהם היא 90°.[3]

מקטבים דיכרואיים (בעלי בליעה סלקטיבית)

מקטבים דיכרואיים (אנ')[א], בולעים אור המקוטב בכיוון מסוים יותר מאשר אור המקוטב בניצב לו. מקטב מסוג זה הוא אנאיזוטרופי באופן בולט ומציג בליעה משמעותית של קיטוב קווי בכוון מסוים בעוד הוא כמעט שקוף לקיטוב בכוון ניצב לו.[3]

מקטבי רשת תיל

מקטב רשת תיל ממיר אלומה לא מקוטבת לאלומה בעלת קיטוב קווי מוגדר. החיצים האדומים מתארים את וקטור השדה החשמלי. אור המקוטב ב"אלכסון" מגיע מצד שמאל באיור. הרכיב האנכי שלו מועבר (מוצג מימין לסריג), בעוד שהרכיב האופקי נבלע או מוחזר.

אחד המקטבים הקוויים הפשוטים ביותר הוא מקטב רשת תיל (באנגלית: wire-grid polarizer, WGP).[3] זה אינו מקטב דיכרואי על פי הגדרתו כי אינו בולע את אחד מכווני הקיטוב אלא מחזיר אותו, אך הוא נכלל בקטגוריה זו מסיבות פדגוגיות כיוון שעקרון הפעולה שלו משותף עם מקטבים דיכרואים נפוצים אחרים.[3]

מקטב זה מורכב ממערך חוטים מתכתיים מקבילים במישור הניצב לכוון התקדמות האלומה. הקיטוב שאינו מועבר אינו נבלע אלא מוחזר ולכן מקטבים מסוג זה יכולים לשמש כמקטבים מפצלי קרן. הבליעה השיורית גבוהה יחסית בהשוואה לרוב המקטבים הדיאלקטריים, אם כי נמוכה בהרבה מאשר במקטבים בולעים. יתרונם בביצועי קיטוב טובים בתחום אורכי גל רחב, בתפקוד טוב גם באלומות מתכנסות (תוך שמירה על ביצועי קיטוב בתחום של אפילו 0-45°) ובהיותם קומפקטיים וקלים לסיבוב.[7] המגבלה באורכי הגל הארוכים נובעת מבליעה על ידי המצע ולא מאבדן ביצועי קיטוב של הרשת, והמגבלה באורכי הגל הקצרים נובעת מהמרחק בין התיילים.[7] כמה סוגים של מקטבי רשת תיל מקטבים היטב בתחום ספקטראלי רחב של 450 עד 2000 ננומטר, עומדים בטמפרטורות של מאות מעלות צלזיוס ובעצמות קרינה של 50 קילוואט לסנטימטר רבוע ללא נזק (אך הם יקרים בהרבה ממקטבי יריעה דיכרואיים).[8]

כאשר רכיב השדה החשמלי של גל אלקטרומגנטי מקביל לחוטים המוליכים, הוא יגרום לתנועת אלקטרונים לאורך החוטים, מה שיוצר זרם חשמלי וכתוצאה גם חום כתוצאה מהתנגשות אלקטרונים.[3] מכיוון שהאלקטרונים חופשיים לנוע בכיוון זה, המקטב מתנהג באופן דומה לפני השטח של מתכת בעת החזרת אור, והגל מוחזר לאחור, מלבד כמות קטנה של אנרגיה שאובדת לחימום החוט.[9][7]

כאשר רכיב השדה החשמלי של הגל הפוגע ניצב לחוטים, האלקטרונים אינם יכולים לנוע מעבר לתנועה לרוחב כל חוט, וכמעט ואין אינטראקציה בין הגל הפוגע לחוטים, הוא עובר ללא הפרעה ולכן רק מעט אנרגיה מוחזרת והגל הפוגע עובר ברובו דרך הרשת.[3][7] במקרה זה הרשת מתנהגת כמו חומר דיאלקטרי.[9]

התנהגות זו גורמת לגל המועבר להיות מקוטב באופן קווי כך שרכיב השדה חשמלי שלו ניצב לחוטים.[7] ההשערה שהגלים "חומקים" דרך הפערים בין החוטים אינה נכונה.[3]

כאשר אורך הגל שווה למרווח בין התיילים, שני רכיבי הקיטוב מועברים.[7] לשימושים מעשיים, המרחק בין החוטים חייב להיות קטן מאורך הגל של הקרינה הפוגעת כדי לתפקד כמקטב, והרשת תתנהג כמקטב יעיל כאשר המרחק בין התיילים קטן מחצי אורך הגל, בקירוב.[7] בנוסף, רוחבו של כל חוט צריך להיות קטן בהשוואה למרחק בין החוטים. לכן, קל יחסית לבנות מקטבי רשת תיל עבור גלי רדיו[7] (כולל גלי מיקרו),[3] ועבור קרינה תת אדומה באורכי גל ארוכים ובינוניים. עבור אופטיקה בתת-אדום הרחוק, ניתן לייצר את המקטב אפילו כרשת עצמאית. באור נראה, יותר קשה לממש מקטב כזה. ב-1960 פורסם ההישג של רשת בצפיפות של 2160 תיילים למילימטר ששימשה כמקטב בתחום התת-אדום.[3] בעזרת טכניקות ליתוגרפיות מתקדמות ניתן גם לבנות רשתות מתכתיות צפופות מאוד (מרווחים טיפוסים בין מרכזים בשיעור של 50–100 ננומטר), מה שמאפשר מימוש מקטב אף באור נראה.[9] מכיוון שמידת הקיטוב תלויה אך מעט באורך הגל ובזווית הפגיעה, מקטבי רשת תיל משמשים ליישומים כגון מקרנים.

גם למקדם השבירה של המצע הנושא את החוטים יש משמעות, והמקטב יתפקד טוב יותר עבור מקדמי שבירה נמוכים יותר.[7] במקרים בהם נחוץ להשתמש במצע בעל מקדם שבירה גבוה, כמו סיליקון או גרמניום, מומלץ להשתמש בציפוי נגד החזרה על המצע לפני נידוף התילים המוליכים, כיוון שמצע המצופה בציפוי מושלם נגד החזרה מתפקד כאילו הרשת תלויה באוויר.[7]

ניתן להשתמש במקטב רשת תיל כמקטב מפצל קרניים יעיל, על ידי הצבתו בזווית לקרן הפוגעת, ומקטב כזה מתפקד היטב גם במפתח נומרי גבוה.[9] מסיבות אלו, משתמשים בו כתחליף למקטב מפצל קרניים מבוסס מנסרה (פריזמה) במקרנים.[9]

גבישים דיכרואיים

גבישים מסוימים הם דיכרואיים, בולעים קיטוב בכוון מסוים אך מעבירים קיטוב ניצב ולכן ניתן להשתמש בהם כמקטבים קוויים.[10] הגביש הידוע ביותר מסוג זה הוא טורמלין.[3] עם זאת, גביש זה משמש לעיתים רחוקות כמקטב, מכיוון שהאפקט הדיכרואי שלו תלוי מאוד באורך הגל, מה שגורם לגביש להראות צבעוני.[10] הרפתיט (אנ') גם הוא דיכרואי, אינו צבעוני מאוד אך עדיין יכול להראות ורוד כשהוא מואר באור לבן בקיטוב מסוים וירוק כשהוא מואר בקיטוב אחר.[10][3] את שני סוגי הגבישים הללו (הרפטיט וטורמלין) קשה לגדל לגבישים גדולים.[10][3] גבישים אלו מתנהגים כמקטבים דיכרואיים כיוון שהכוחות האלסטיים שקושרים את האלקטרונים בחומר אינם סימטריים.[3]

מקטבי יריעה דיכרואיים

סוג המקטב הנפוץ ביותר הוא מקטב יריעה דיכרואי (dichroic sheet polarizer), העשוי לרוב ממצע פולימר ובו מולקולות צבע או גבישים הבולעים אור המקוטב לאורך הציר הארוך של המולקולות.[8]

הגרסה הראשונה של מקטב פולארויד פותחה על ידי אדווין לאנד (אנ') (מייסד פולארויד) וצוותו בשנת 1930 ונקרא יריעת-J.[7] מקטב זה הכיל גבישי הרפתיט סב-מיקרוסקופיים ומקבילים זה לזה, מוטמעים ביריעת צלולוז-אצטט, ותפקדה כגביש דיכרואי שטוח.[3][7] חסרונו של פתרון זה היה בנטייתו לפזר את האור העובר, בגלל הפיזור מהגבישים הזעירים, ולכן נראה מעורפל.[7][3] צורתו הנוכחית של הפולארויד הומצאה ב-1938 על ידי אותה קבוצה, נקראה יריעת-H והיא עשויה מפלסטיק פוליוויניל אלכוהול (PVA) עם כמויות זעירות של יוד.[7][10] מקטב זה מתפקד באופן דומה בקנה מידה אטומי למקטב רשת-תיל וניתן לחשוב עליו בתור הגרסה הכימית שלו.[1][3] חימום ומתיחת היריעה בכוון מסוים במהלך הייצור גורמת לשרשראות ה-PVA הארוכות להתיישר בכיוון המתיחה.[10] בשלב זה טובלים את היריעה בתמיסת יוד, מולקולות היוד מתחברות למולקולות ה-PVA והופכות אותן למוליכות לאורכן.[10] אלקטרונים ערכיים מאטומי היוד מסוגלים לנוע באופן ליניארי לאורך שרשראות הפולימר, אך לא לרוחבן ולכן, אור פוגע המקוטב במקביל לשרשראות נבלע על ידי היריעה; אור המקוטב בניצב לשרשראות מועבר דרכה.[10]

העמידות והפרקטיות של פולארויד הופכות אותו לסוג המקטב הקווי הנפוץ והזול ביותר בשימוש, למשל עבור משקפי שמש, מסנני צילום וצגי גביש נוזלי (למשל מסכי מחשב), והם זמינים בממדים של מעל מטר רבוע.[1][10][8] למקטבים אלו סף נזק[ב] נמוך של כ-1 ואט לסנטימטר רבוע כיוון שהם בולעים את הקיטוב שאינו רצוי והם אינם סובלים כלל מהפיזור המוגבר של יריעת ה-J כיוון שממדי המולקולות קטנים מכדי לגרום פיזור.[8][7][3]

ישנן ווריאציות נוספות של מקטבים כאלו המתוכננות לעמידות גבוהה יותר ללחות ולטמפרטורות גבוהות, לתחומים ספקטראלים שונים ולביצועים שונים, ומגוון מקטבים כאלו מיוצרים על ידי יצרנים שונים.[7] למולקולות הצבע יש תחום אורכי גל מוגבל בו הן מקטבות היטב, וישנן שתי קטגוריות עיקריות: 400 עד 750 ננומטר, כאשר הן בולעות את כל הקיטובים מתחת ל-400 ננומטר ומעבירות את כל הקיטובים מעל 750 ננומטר, ובתחום של 800 עד 2000 ננומטר כאשר באופן דומה לתחום אורכי הגל הנמוך יותר, רוב האור מתחת ל-800 ננומטר נבלע ומעל 2000 ננומטר כולו נבלע, ללא תלות בקיטוב.[8] יחס ההכחדה נחשב טוב באופן מפתיע ביחס למחיר.[8] ניתן לשפר את עיוותי חזית הגל (wavefront distortion) על ידי שימוש בזכוכית כחומר מצע במקום פולימר, אך מימוש זה מעלה את מחיר המקטב.[8]

חסרונו של פולארויד הוא בעמידות בקרינה על סגולה.[7] דוגמה אחת להתמודדות עם חיסרון זה היא טכנולוגיה דומה של מקטב מולקולרי, בשם פולאקואט (Polacoat), שממומשת על מצע של פלסטיק או זכוכית, ומתפקדת היטב בתחום רחב בין על סגול ועד תת-אדום קרוב.[11][7]

סוג מודרני של מקטב בליעה בשם פולרקור (Polarcor) עשוי מננו-חלקיקי כסף מוארכים המוטבעים בשכבת זכוכית דקה של פחות מחצי מילימטר.[12] מקטבים אלה עמידים יותר, יכולים לקטב אור טוב בהרבה ממסנן פולארויד פלסטי, ומשיגים יחסי קיטוב של עד 1:100,000 ובליעת אור מקוטב נמוכה עד כדי 1.5% (בתת אדום), כאשר הוא מקוטב בכוון הנכון עבור תפקוד הפילטר.[12] מקטבי זכוכית כאלה מתפקדים בצורה הטובה ביותר עבור אור באורכי הגל הארוכים יותר של האינפרא אדום, ונמצאים בשימוש נרחב בתקשורת סיבים אופטיים.

מקטבים מפצלי קרניים

מקטבים מפצלי קרניים מפצלים את הקרן הפוגעת לשתי אלומות בעלות קיטוב ליניארי שונה. עבור מפצל אלומה אידיאלי, שתי האלומות הללו תהיינה מקוטבות באופן מושלם, עם קיטובים ניצבים. אולם במקרים רבים מפצלי אלומה נפוצים אינם מושלמים ורק אחת משתי האלומות מקוטבת באופן מושלם, והשנייה מכילה תערובת של מצבי קיטוב.

בניגוד למקטבים בולעים, מקטבים מפצלי אלומה אינם צריכים לבלוע ולפזר (אנ') את האנרגיה של מצב הקיטוב הלא רצוי, ולכן הם מתאימים יותר לשימוש עם אלומות בעלות עוצמה גבוהה כמו אור לייזר. מפצלי אלומה הקרובים לשלמות שימושיים גם כאשר יש לנתח מערכת או להשתמש בשני רכיבי הקיטוב בו זמנית.

קיטוב על ידי החזרת פרנל - "ערימה של לוחות"

ערכים מורחבים – חוקי פרנל, זווית ברוסטר
גרפים של החזרה כפונקציה של זווית פגיעה. קיטוב p מסומן באדום, קיטוב s מסומן בכחול.
הגרף השמאלי מראה החזרה בתווך בין אוויר לחומר (כמו זכוכית) בעל מקדם שבירה של 1.5. הזווית בה ההחזרה של רכיב ה-p מתאפסת היא זווית ברוסטר.
הגרף הימני מראה החזרה בתווך בין חומר (זכוכית) בעל מקדם שבירה של 1.5 לאוויר. הגרף מדגים כי זווית ברוסטר בחומר נמוכה מבאוויר. הזווית הקריטית, בה (ומעליה) מתרחשת החזרה פנימית מלאה מסומנת בקו אופקי.

ניתן לייצר מקטב ליניארי פשוט על ידי מערך לוחיות שקופות המוטות בזווית ברוסטר ביחס לאלומה הפוגעת. מערך זה מכונה "ערימה של לוחות" ("pile of plates"). זו היא קטגורית המקטבים הגדולה ביותר הנמצאת בשימוש בתת-אדום ובעל-סגול (כאשר אי אפשר להשתמש במקטבי יריעה דיכרואים או במנסרות קלציט), ונמצאת בשימוש גם באור נראה.[13] בתחום התת-אדום משתמשים בלוחיות העשויות מהמוליכים למחצה סיליקון, גרמניום וסלניום.[13] האור פוגע בערימת הלוחות בזווית שאינה זווית ישרה ויש שימוש בשיטה זו גם בהחזרה וגם בהעברה.[13] כיוון שמרבית המקטבים הללו מתפקדים בזוויות קרובות לזווית ברוסטר, הם נקראים גם מקטבי זווית ברוסטר.[13]

על פי נוסחאות החזרת פרנל, כאשר אור מוחזר מממשק בין שני חומרים שקופים, ההחזרה שונה עבור אור המקוטב במישור הפגיעה (אנ') מאשר עבור אור המקוטב בניצב לו. אור המקוטב במישור הפגיעה נקרא מקוטב ב-p, בעוד שאור המקוטב בניצב לכך נקרא מקוטב ב-s. בזווית מיוחדת המכונה זווית ברוסטר, לא מוחזר כל אור בקיטוב p מהממשק, ולכן כל האור המוחזר חייב להיות מקוטב ב-s. אור זה הוא בעל שדה חשמלי ניצב למישור הפגיעה.

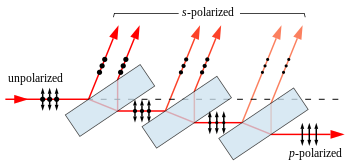
"ערימה של לוחות" המונחים כך שאלומת אור תפגע בכל אחת מהן בזווית ברוסטר. כיוון שפגיעה בזווית זו גורמת להחזרה של חלק מהאור בקיטוב s מלא מכל מממשק, היא משאירה אלומת אור מקוטבת חלקית ב-p. החיצים האדומים מיצגים את אלומת האור המתקדמת משמאל לימין ומתפצלת בכל מכל מממשק לרכיב מוחזר ולרכיב מועבר. החיצים השחורים מצביעים על כיוון השדה החשמלי. עיגול מסמל חץ הניצב למישור המסך, שהוא קיטוב s בדוגמה זו. קיטוב p מלא בזווית ברוסטר דורש הרבה יותר לוחות מהמוצג באיור.

האור שאינו מוחזר מכל ממשק, מועבר דרכו (בהנחה של אפס בליעה).

בזווית מיוחדת זו, חלק מהאור המקוטב ב-s מוחזר מכל ממשק של כל לוח, אך ההחזרה לא מכילה אף לא שביב אור המקוטב ב-p.[14] עבור מערך לוחיות כזה, כל החזרה מדללת את האור העובר דרכן מאור המקוטב ב-s ולכן משאירה באלומה המועברת חלק גדל והולך של אור מקוטב ב-p. עבור אור נראה באוויר ומערך העשוי מזכוכית טיפוסית, זווית ברוסטר היא כ-56°, ועבור כל ממשק אוויר-זכוכית או זכוכית-אוויר, מוחזר כ־15% מקיטוב s הקיים באלומה.[15][16] בשיטה זו נדרשות לוחיות רבות כדי להשיג אפילו קיטוב p בינוני של האלומה המועברת. עבור מערך של 10 לוחיות מתקיימות 20 החזרות ולכן מועבר רק כ-4% (1−15/100)20= של האור המקוטב ב־s. ככל שמקדם השבירה גבוה יותר, ידרשו פחות לוחיות לאותה רמת קיטוב בהעברה.[13]

ככל שהזווית בה פועל המקטב גדלה, כך גדל גם גודלו הפיזי של המקטב.[ג]

הקרן המוחזרת, אף על פי שהיא מקוטבת s במלואה, משתרעת על פני שטח גדול ועשויה לא להיות שימושית במיוחד. דוגמה לכך הוא גרמניום בתת-אדום למשל, עבורו זווית ברוסטר היא 76°, גבוהה משמעותית משל זכוכית באור נראה.[13] לכן במקרה בו קוטר האלומה הוא 25 מילימטר תצטרך כל לוחית גרמניום להיות לפחות בגודל של 25 על 100 מילימטר, ואם מדובר בשימוש ברכיב s, בהחזרה, שלוש לוחיות כאלו ידרשו מקטב באורך של מעל 200 מילימטר.[13]

ניתן להשיג קרן מקוטבת שימושית יותר על ידי הטיית מערך הלוחיות בזווית תלולה יותר ביחס לקרן הפוגעת. באופן לא אינטואיטיבי, שימוש בזוויות פגיעה גדולות מזווית ברוסטר מניב דרגת קיטוב גבוהה יותר של הקרן המועברת, על חשבון העברה כוללת מופחתת. עבור זוויות פגיעה תלולות מ-80°, הקיטוב של הקרן המועברת יכול להתקרב ל-100% עם ארבע לוחיות בלבד, אם כי עוצמת ההעברה נמוכה מאוד במקרה זה. הוספת לוחות נוספים והפחתת הזווית מאפשרות השגת פשרה טובה יותר בין העברה לאיכות קיטוב.

מקטבים בעלי שבירה כפולה

ערך מורחב – שבירה כפולה

בראשית המאה ה-19 הדרך הידועה היחידה ליצירת אור מקוטב הייתה באמצעות גביש קלציט, ששימש אז לפיתוח חוק מאלוס.[17] לגבישים כמו קוורץ וקלציט תכונות שבירה הכפולה המאפשרות לנצלם כמקטבים. בגבישים אלה, קרן אור לא מקוטב הפוגעת בפני השטח שלהם מתפצלת על ידי שבירה לשתי קרניים, קרן רגילה (קרן o), וקרן המכונה יוצאת דופן (קרן e). חוק סנל מתקיים כרגיל עבור שתי הקרניים הללו, כאשר שבירה כפולה משמעותה כי מקדם השבירה שונה לכל קרן. באופן כללי שתי הקרניים תהיינה במצבי קיטוב שונים, אם כי לא במצבי קיטוב קוויים למעט כאשר הן מתקדמות בכיווני התפשטות מסוימים יחסית לציר הגביש. ישנן דרכים רבות לנצל את העובדה שישנם שני מקדמי שבירה שונים בגביש כדי להפריד את גלי ה-o מגלי ה-e.[3] כמעט כל המנסרות המקטבות המשמשות לאור נראה, על-סגול קרוב ותת-אדום קרוב עשויות מקלציט, שלו שבירה כפולה חזקה בתחום אורכי גל רחב, ומגבישים אחרים עבור תחומים ספקטראליים אותם קלציט אינו מעביר.[18]

פריזמת ניקול: הזווית בין שני חלקיה נבחרת כך שהקרן בקיטוב שניצב למישור האיור תחווה החזרה פנימית מלאה בממשק הדבק, ולכן תוסט לצד הגביש (בכוון מעלה באיור), בעוד הקרן בעלת הקיטוב הניצב תמשיך בדרכה כיוון שמקדם השבירה שלה אינו מקיים את תנאי ההחזרה הפנימית המלאה.

פריזמת ניקול הייתה סוג מוקדם ונפוץ של מקטב שבירה כפולה, שהורכב מגביש קלציט אשר נחצה וחובר מחדש עם בלסם קנדי (אנ') אשר שימש כדבק אופטי בעל מקדם שבירה המצוי בין מקדמי השבירה של o ו-e.[3][18] הגביש נחתך כך שקרני ה־o וה- e נמצאות במצבי קיטוב ליניאריים ניצבים זה לזה. קרן פוגעת בגביש נשברת לפי חוק סנל ומתפצלת לקרן o ולקרן e, כפי שרואים באיור משמאל. קרן ה־o חווה החזרה פנימית מלאה בממשק הבלסם, מכיוון שהיא מגיעה אליו בזווית גדולה מהזווית הקריטית עבורה, והיא מוסטת לצד הגביש ונבלעת על ידי שכבה של צבע שחור על צד הגביש.[3] באותה דוגמה קרן ה־e חווה מקדם שבירה קטן יותר, פוגעת בממשק בזווית קטנה יותר ולכן לא חווה החזרה פנימית מלאה אלא מועברת דרך הממשק.[3] פריזמות ניקול הוחלפו לאורך השנים במקטבים אפקטיביים יותר.[3]

פריזמות ניקול מייצרות אור מקוטב ברמה גבוהה, והיו בשימוש נרחב במיקרוסקופיה, אם כי עקב חסרונות כמו קיטוב משתנה לרוחב שדה הראייה וחסרונות נוספים, הן הוחלפו בעיקר בחלופות טובות יותר אופטית כגון פריזמת גלן-תומפסון (אנ'), פריזמת גלן-פוקו (אנ') ופריזמת גלן-טיילור (אנ').[18]

פריזמת וולסטון

יחס ההכחדה הטוב ביותר שניתן להשגה עם פריזמת גלן-תומפסון הוא הטוב מכל המקטבים ועומד על 5:100,000 ואפילו 1:1,000,000 ואף יותר.[18]

כאמור למעלה, ישנן ווריאציות רבות של פריזמות מקטבות. הבלסם הקנדי (כמו סוגי דבק אחרים) בולע בעל-סגול, ולכן מגביל את השימוש, אבל הקלציט עצמו שקוף בתחום אורכי הגל מ-230 ננומטר בעל סגול עד 5000 ננומטר בתת-אדום, לכן פריזמות בעלות מרווח אוויר טובות לשימוש גם באורכי הגל הקצרים.[3][18] פריזמת ניקול שעשויה מקלציט בלבד, עם מרווח אוויר במקום הבלסם הקנדי נקראת פריזמת פוקו.[18] פריזמת גלן-פוקו עשויה מקלציט בלבד, עם מרווח אוויר במקום הבלסם הקנדי אבל מורכבת בחיתוך שונה של ציר הגביש.[3][18]

ישנן גם פריזמות מפצלות קרניים, שמאפשרות לשתי קרניים בקיטובים ניצבים לצאת מהמקטב כשהן מופרדות במרחב.[18] זו אינה הבחנה מוחלטת כיוון שכל פריזמה מקטבת ניתנת להפיכה לפריזמה מקטבת מפצלת קרניים על ידי שינוי הזווית של אחת מפיאותיה או על ידי הסרת הצבע הבולע ממנה.[18]

פריזמת וולסטון (אנ') היא דוגמה למקטב מפצל קרניים מבוסס שבירה כפולה המקטב היטב גם על-סגול של ריק.[ד][18] היא מורכבת משתי מנסרות קלציט משולשות עם צירי גביש ניצבים המחוברות יחד. בממשק הפנימי, קרן לא מקוטבת מתפצלת לשתי קרניים מקוטבות קווית אשר יוצאות מהפריזמה בזווית סטייה סימטרית של בין 15° ל-45°. פריזמת נומרסקי היא גרסה של פריזמת וולסטון, הנמצאת בשימוש נרחב במיקרוסקופיית ניגודיות התאבכות דיפרנציאלית.[19]

מקטבי שכבות דקות

ערך מורחב – התאבכות משכבות דקות

מקטבים קוויים שיוצרו בטכנולוגיית שכבות דקות (הידועים גם בשם TFPN) הם מצעים מזכוכית עליהם ציפוי שכבות דקות שמקדמי השבירה והעובי שלהן נבחרו בקפידה כדי ליצור התאבכות בונה (או הורסת).[13] מקטבים אלו משמשים בדרך כלל בזויות פגיעה שאינה זווית ישרה[13] ומתפקדים כמקטב "ערימה של לוחות" בעל ביצועים משופרים עקב ההתאבכות.[8] הם תמיד יעבירו קיטוב p ויחזירו קיטוב s.[8] בזווית ברוסטר עדיין ההחזרה בקיטוב p היא אפס (הכל מועבר) אבל הציפוי יכול לשנות את עצמת ההחזרה (וההעברה) בקיטוב s, וכך לשפר את ביצועי המקטב או לצמצם את כמות הלוחות הנדרשים ביחס למקטב דומה שאינו מנצל התאבכות.[13] עם זאת, יש חיסרון והוא רגישות מוגברת לשינויים בזווית הפגיעה.[13]

דוגמה למקטב מפצל קרניים המורכב משתי מנסרות של 45°-90°-45° מודבקות זו לזו ליצירת קובייה. לצורך הדוגמה, האילוסטרציה מסמנת ב-V את קיטוב ה-s וב-H את קיטוב ה-p.

המצע יכול להיות לוחית, הממוקמת בזווית מסוימת לקרן, או מנסרת זכוכית המודבקת למנסרה שנייה ליצירת קובייה כאשר הציפוי מצוי על האלכסון (היתר).[13] האור פוגע בניצב לפאת הקובייה אך בזווית למישור הציפוי (שהוא היתר של המנסרה). הקרן המועברת היא מקוטבת p כמעט לחלוטין והקרן המוחזרת (אשר בגלל הגאומטריה, יוצאת מצד הקובייה) מקוטבת s כמעט במלואה[ה].[13] במימוש בו צופו משטחי שתי המנסרות, משני צידי הדבק, בחמש שכבות כל אחת, באור לבן, התקבל קיטוב טוב מ-98% על פני תחום זוויות של מעל 5° הן לרכיב המועבר והן למוחזר.[13] בדרך כלל מצפים רק את היתר של אחת המנסרות בשכבות בעובי רבע גל של חומרים בעלי מקדם שבירה גבוה ונמוך לחליפין.[8] קוביות כאלו יכולות לעמוד בצפיפות קרינה 500 ואט לסנטימטר רבוע, כאשר המגבלה היא בדרך כלל עמידות הדבק, ולא הציפוי, ולכן שימוש בהדבקת מגע אופטית (אנ') ישפר את העמידות.[8]

בדרך כלל מקטבים מפצלי קרניים מתוכננים כך שיוציאו את שני רכיבי הקיטוב בזווית ישרה זה לזה.[13]

מקטבים מבוססי שכבות דקות בדרך כלל אינם מתפקדים טוב כמו מקטבים מסוג גלן, אך הם זולים ומספקים שתי אלומות מקוטבות טוב, פחות או יותר באותה מידה. מקטבים מסוג קובייה בדרך כלל מתפקדים טוב יותר ממקטבי לוחית. למקטב קובייה יחס הכחדה של מעל ל-1:1000 עבור הקרן המועברת, אבל פחות מ-1:100 לקרן המוחזרת.[8] דרך פשוטה לשיפור היא על ידי הוספת מקטב ניקוי: מקטב יריעה דיכרואי, לאחר שקרן ה-s המוחזרת יוצאת מהקובייה.[8]

בגלל צורתם החיצונית, קל לבלבל בין מקטבי קובייה מבוססי שכבות דקות ומקטבי קובייה מבוססי שבירה כפולה.

מקטבים מעגליים

מקטבים מעגליים ( CPL - circular polarizing filters) יכולים לשמש ליצירת אור מקוטב בקיטוב מעגלי או לחלופין לבליעה סלקטיבית או להעברה סלקטיבית של אור מקוטב מעגלית, אם זה בכיוון השעון או נגד כיוון השעון.

מקטב מעגלי הומוגני

מימוש מקטב מעגלי הומוגני באמצעות לוחית רבע גל שאחריה מקטב קווי ולוחית רבע גל מסובבת ב-90° ביחס לראשונה.

אלמנט קיטוב הומוגני הוא אלמנט שבו מצבי מינימום ומקסימום ההעברה הם ניצבים.[20] רכיב כזה יכול להיות ליניארי, מעגלי או אליפטי.[20]

מקטב מעגלי הומוגני מעביר קיטוב מעגלי מסוים (למשל: שמאלי) ללא שינוי וחוסם את הקיטוב ההפוך (למשל: ימני). התנהגות זו דומה לאופן שבו מקטב קווי יעביר במלואה זווית אחת של אור מקוטב קווית ללא שינוי, אך יחסום לחלוטין כל אור מקוטב ליניארי שניצב לכוון זה. ניתן ליצור מקטב מעגלי הומוגני על ידי הצבת מקטב קווי בין שתי לוחיות רבע גל.[21] כאשר פוגע אור מקוטב מעגלית בלוחית רבע הגל הראשונה, אחד מרכיבי השדה החשמלי שלו מעוכב ברבע אורך גל יחסית לרכיב הניצב לו, מה שיוצר קיטוב קווי. המקטב הקווי המונח בין לוחיות רבע הגל מכוון כך שיעביר קיטוב קווי אחד וייחסום את הניצב לו. לוחית רבע הגל השנייה מקבלת את האור המקוטב קווית שעבר את ההתקן ומעכבת את הרכיב הניצב, זה שלא עוכב על ידי הלוחית הקודמת. דבר זה מחזיר את שני הרכיבים ליחסי הפאזה הראשוניים שלהם, ומחזיר את הקיטוב המעגלי שנבחר. הכנסת קיטוב מעגלי הפוך (ימני בדוגמה שבאיור) תפיק לאחר לוחית הגל הראשונה קיטוב קווי ניצב לזה שמתואר באיור, שיחסם לחלוטין על ידי המקטב הקווי שבאמצע ההתקן.

מקטבים טבעיים: החזרה ופיזור

ערך מורחב – פיזור
הקרינה המפוזרת בשמיים היא מקוטבת: התמונה מימין צולמה דרך מקטב שסובב כדי להגיע למינימום עוצמה.

רוב הקרינה האלקטרומגנטית בטבע אינה מקוטבת[22] אבל יש קיטוב של אור המופיע בטבע בעיקר דרך תהליכי החזרה ופיזור. כפי שהוסבר בפרק קודם, כאשר אור פוגע במשטח לא־מתכתי, כמו מים, ההחזרה גורמת לכך שהאור המוחזר מקוטב חלקית (ומקוטב לחלוטין אם ההחזרה היא בזווית ברוסטר).[3]

בנוסף, פיזור של אור השמש באטמוספירה על־ידי מולקולות או חלקיקים קטנים (פיזור ריילי) גורם לכך שהאור בשמים מקוטב קווית, בעיקר בכיוון ניצב לקרן השמש, ותופעה זו תוארה לראשונה בסוף המאה ה־19 על־ידי לורד ריילי.[3][23] האור שמגיע מהשמש הוא במקורו בלתי-מקוטב. כלומר, כוון השדה החשמלי הוא אקראי (אך ניצב לכיוון התקדמות האור, בהיותו גל רוחבי). כאשר אור זה פוגע במולקולות באטמוספירה, מתרחש פיזור: הפוטונים גורמים לאלקטרונים במולקולות להתנודד ולפלוט קרינה משנית בכוון השדה החשמלי, בעיקר בניצב לכיוון התנודה של האלקטרון. לכן כדי שהקרינה תגיע לצופה מהצד היא חייבת להגיע ממולקולות שמתנודדות בכוון שפולט אנרגיה לכוונו ולא מאלו הניצבות, לכן היא מקוטבת.[24][25]

ישנם מקטבים טבעיים בבעלי חיים, כמו החיפושית נחושתית הוורדים שהשריון שלה הוא מקטב אליפטי[ו] שמאלי.[26]

שימושים למקטבים

משקפי שמש ומסכים

אנימציה של העברת אור דרך מקטב קווי המחזק מול צג מחשב מסוג מסך גביש נוזלי. מסכים אלו פולטים אור מקוטב קווית כך שכאשר ציר המקטב ניצב לקיטוב האור מהמסך, האור נחסם והמקטב נראה שחור. כאשר הוא מקביל לקיטוב האור מהמסך, המקטב מאפשר לאור לעבור והמסך הלבן נראה גם דרך המקטב.

מכיוון שאור המוחזר ממשטחים אופקיים מקוטב אופקית, כדי להקטין את עצמת האור המסנוור מומלץ לנהגים להרכיב משקפי שמש עם מקטב (פולרואיד) המכוון אנכית.[27]

מסכי גביש נוזלי נפוצים כמו מסכי מחשב, טלוויזיות וטלפונים חכמים משתמשים בדרך כלל בזוג מקטבי יריעה שטוחים כחלק חיוני בפעילותם.[28] למשל, הגבישים הנוזליים ממוקמים בין זוג מקטבים ניצבים. כל פיקסל בגביש הנוזלי שולט במידת סיבוב השדה כך שאם הוא לא משנה את קיטוב האור העובר דרכו, הוא יחסם במקטב הניצב, סיבוב חלקי יעביר עצמת אור חלקית (לפי חוק מאלוס) וסיבוב ב-90° יאפשר למלוא העצמה של אותו פיקסל לעבור.[29]

משקפי תלת־ממד

מקטבים מעגליים משמשים כעדשות של משקפי תלת-ממד לצפייה בסרטים סטריאוסקופיים מסוימים (בעיקר, גרסה תלת-ממדית של RealD 3D (אנ')), שבהם הקיטוב של האור משמש להבחנה איזו תמונה צריכה להיראות על ידי עין שמאל ואיזו על ידי עין ימין.

לייזרים

מראות המהוד של ליזר גאזי מוצבות בזווית ברוסטר, לכן הן מחזירות ומשמרות את קיטוב p בתוך המהוד.[30]

מיקרוסקופיה

מיקרוסקופ מקטב הוא מיקרוסקופ המשלב מקטב ועובד בהחזרה או בהעברה.[31] הוא משמש בתחומים כמחקר מינרלים, ביולוגיה, רפואה, כימיה פולימרית, גבישים נוזליים, זיכרון מגנטי ועוד.[31]

מדידת מאמצים בחומר

מאמצים פנימיים במד-זווית מפלסטיק מתגלים בבדיקה בין מקטבים.

בהתאם לחוק מאלוס, על ידי הנחת דגימה מזכוכית או פלסטיק בין מקטבים קווים ניצבים ניתן לצפות במאמצים שיוריים בחומר כיוון שחומרים אלו משנים את קיטוב האור תחת מאמץ.[32] התופעה תלויה באורך הגל, ולכן התמונה המתקבלת צבעונית למדי.[32]

צילום

בצילום משתמשים במקטב המותקן לפני העדשה כדי לצמצם את השפעות ההחזרות ממשטחים מבריקים ולצלם עצמים המצויים מאחרי חלון זכוכית (כמו חלון ראווה או שמשת רכב) או או שקועים במים (כמו קרקעית של שלולית) ללא ההשתקפויות מהסביבה או להפך, כדי לצלם רק את ההשתקפויות, בתלות בכוונון זווית המקטב.[33] מסנני קיטוב קוויים היו סוגי המקטבים הראשונים ששימשו בצילום, ועדיין ניתן להשתמש בהם בחלק ממצלמות הרפלקס (SLR). עם זאת, מצלמות בעלות מערכות מדידה דרך העדשה (TTL) ומערכות מיקוד אוטומטי - כלומר, כל מצלמות ה-SLR וה- DSLR המודרניות - מסתמכות על אלמנטים אופטיים המעבירים אור מקוטב קווית. אם האור הנכנס למצלמה כבר מקוטב קווית, הוא עלול לשבש את פעילות מערכות החשיפה או המיקוד האוטומטי. לכן עלתה הפופולריות של מסנני קיטוב מעגליים, כיוון שהם מנחיתים אור מקוטב קווית ובכך יכולים לשמש כדי להחשיך שמיים, לשפר את הרוויה ולהסיר החזרות לא רצויות, אך האור המקוטב מעגלית שהם מעבירים אינו משבש את פעולת המערכות הללו.[34]

פולרימטרייה במכ"ם

במדידת קיטוב (פולרימטרייה) לצורך מיפוי בתחומים כמו חקלאות, יערות, גאולוגיה, הידרולוגיה או אוקיינוגרפיה משתמשים בגלי מיקרוגל ששודרו ונקלטו בקיטובים שונים.[35] גם אורך הגל וגם הקיטוב משפיעים על האופן שבו מערכת מכ"ם "רואה" את האלמנטים בזירה ולכן, תמונות מכ"ם שנאספו באמצעות שילובי מקטבים קוויים (הן מקבילים והן מוצלבים) עם אורכי גל שונים מספקים מידע מפורט על פני השטח.[35]

לוחמה אלקטרונית

מקטבים מסוגים שונים, גם קוויים וגם מעגליים, משמשים בלוחמה אלקטרונית החל משנות ה-80 של המאה העשרים.[36][37][38] התאמת הקיטוב של המערכת הקולטת לקיטוב המטרה משפרת את טווח הגילוי ואת תפקוד המערכת.[38] מערכות המשתמשות במקטבים מאפשרות קליטה של אותות המשודרים מקיטובים מגוונים. כמו כן המקטבים מאפשרים שיבוש של מכמ"ים בקיטובים שונים (שאלמלא כן, יכלו לשבש רק מכ"מים בקיטוב תואם).[39][40]

ראו גם

לקריאה נוספת

Eugene HECHT, Alfred ZAJAC, 8.2 Polarizers, OPTICS, 4th edition, Addisin-Wesley, 1974, מסת"ב 0-201-02835-2

קישורים חיצוניים

ביאורים

  1. ↑ המילה "דיכרואי" משמשת גם בשלוש דרכים נוספות: (1) כדי לציין את השינוי בצבע של תמיסת צבע עם שינוי בריכוז, (2) כדי לציין מסנן צבע בעל שני פסי העברה בחלקים שונים מאוד של התחום הנראה ולכן הוא משנה צבע כאשר ההתפלגות הספקטרלית של מקור האור משתנה ו-(3) כדי לציין מסנן התאבכות שנראה בצבע שונה כאשר הוא מוצג באור מוחזר או מועבר.[6]
  2. ↑ סף נזק מתאר את עצמת הקרינה המקסימלית לפני היווצרות נזק בלתי הפיך בהתקן. בדרך כלל בשימוש לקרינת לייזר.
  3. ↑ זאת כיוון שהיטל האלומה על הלוחית גדל עם קוסינוס הזווית
  4. ↑ vacuum ultraviolet, אורכי גל מאוד קצרים
  5. ↑ הקיטובים s, p מוגדרים על פי משטח המגע בין המנסרות.[8]
  6. ↑ המצב הכללי של קיטוב הוא קיטוב אליפטי. קיטוב מעגלי וקווי הם מקרים פרטיים שלו.

הערות שוליים

  1. ^ 1.0 1.1 1.2 1.3 1.4 Gåsvik, Kjell J. (2003). Optical Metrology (3rd ed.). John Wiley and Sons. pp. 219–221. ISBN 0470846704.
  2. ↑ Sönke Johnsen, The Optics of Life: A Biologist's Guide to Light in Nature, Princeton University Press, 2012, עמ' 208, מסת"ב 978-0-691-13991-3
  3. ^ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 3.18 3.19 3.20 3.21 3.22 3.23 3.24 3.25 3.26 3.27 Eugene HECHT, Alfred ZAJAC, 8.2 Polarizers, OPTICS, 4th edition, Addisin-Wesley, 1974, עמ' 225-229, 237-238, 242, מסת"ב 0-201-02835-2
  4. ↑ Malus's Law | Optipedia, spie.org, Excerpt from Field Guide to Polarization
  5. ↑ Kjell J. Gåsvik, Optical Metrology, John Wiley & Sons, 2003-04-11, עמ' 219-221, מסת"ב 978-0-470-84670-4
  6. ↑ Handbook of Optics, Volume II - Devices, Measurements, and Properties, עמוד 3.26
  7. ^ 7.00 7.01 7.02 7.03 7.04 7.05 7.06 7.07 7.08 7.09 7.10 7.11 7.12 7.13 7.14 7.15 7.16 7.17 MICHAEL BASS, Editor in Chief, Handbook of Optics, Volume II - Devices, Measurements, and Properties (עמ' 3.27-3.28, 3.30, 3.32), Sponsored by the OPTICAL SOCIETY OF AMERICA, ‏1995
  8. ^ 8.00 8.01 8.02 8.03 8.04 8.05 8.06 8.07 8.08 8.09 8.10 8.11 8.12 8.13 Robert E. Fischer, Biljana Tadic-Galeb, Paul R. Yoder, Polarization Issues in Opical Design (19), Optics System Design, 2, United States of America: McGrew-Hull, 2008, עמ' 535-538, מסת"ב 978-0-07-147248-7
  9. ^ 9.0 9.1 9.2 9.3 9.4 X. J. Yu, H. S. Kwok, Optical wire-grid polarizers at oblique angles of incidence, Journal of Applied Physics 93, 2003-04-15, עמ' 4407–4412 doi: 10.1063/1.1559937
  10. ^ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 Myeongkyu Lee, Polarization, Taylor & Francis, Published in Myeongkyu Lee, Optics for Materials Scientists, 2019, ‏2019 (באנגלית)
  11. ↑ 5.3 Polarimetry - HST User Documentation, hst-docs.stsci.edu
  12. ^ 12.0 12.1 "Polarcor glass polarizers: Product information" (PDF). Corning.com. בדצמבר 2006. אורכב מ-המקור (PDF) ב-2007-10-12. נבדק ב-2008-08-08. {{cite web}}: (עזרה)
  13. ^ 13.00 13.01 13.02 13.03 13.04 13.05 13.06 13.07 13.08 13.09 13.10 13.11 13.12 13.13 13.14 MICHAEL BASS, Editor in Chief, Handbook of Optics, Volume II - Devices, Measurements, and Properties (עמ' 3.36, 3.40, 3.42, 3.43, 3.45), cdn.preterhuman.net, Sponsored by the OPTICAL SOCIETY OF AMERICA, ‏1995
  14. ↑ Introduction to Polarization, www.edmundoptics.ca (באנגלית)
  15. ↑ Brewster’s law | Definition, Formula, Diagram, & Facts | Britannica, www.britannica.com
  16. ↑ The Fresnel Equations and Brewster's Law (עמ' 4), users.physics.ox.ac.uk
  17. ↑ Malus's Law | Optipedia, spie.org, Excerpt from Field Guide to Polarization
  18. ^ 18.00 18.01 18.02 18.03 18.04 18.05 18.06 18.07 18.08 18.09 Michael Bass Editor in Chief, Handbook of Optics, Volume II - Devices, Measurements, and Properties (עמ' 3.2, 3.7, 3.9, 3.10, 3.17, 3.21), Sponsored by the OPTICAL SOCIETY OF AMERICA, ‏1995
  19. ↑ Phase Contrast and Differential Interference Contrast Microscopy, JoVE
  20. ^ 20.0 20.1 MICHAEL BASS, Editor in Chief, Handbook of Optics, Volume II - Devices, Measurements, and Properties (עמ' 22.7), cdn.preterhuman.net, Sponsored by the OPTICAL SOCIETY OF AMERICA, ‏1995
  21. ↑ MICHAEL BASS, Editor in Chief, Handbook of Optics, Volume II - Devices, Measurements, and Properties (עמ' 22.19), cdn.preterhuman.net, Sponsored by the OPTICAL SOCIETY OF AMERICA, ‏1995
  22. ↑ רמי אריאלי, 7.5 קיטוב קרינה אלקטרומגנטית - לייזרים ויישומיהם, באתר לייזרים ויישומיהם - מכון ויצמן, ‏4 בדצמבר 2016
  23. ↑ רמי אריאלי, 4. קיטוב על ידי פיזור - לייזרים ויישומיהם, באתר לייזרים ויישומיהם - מכון ויצמן, ‏4 בדצמבר 2016
  24. ↑ The polarization of the sky, polarization.com
  25. ↑ Vektorfeld (2025-07-01), Why the sky is polarized: see it at home! | Tyndall effect #SoME4, p. דקה 7, נבדק ב-2025-10-05
  26. ↑ Hans Arwin, Roger Magnusson, Jan Landin, Kenneth Järrendahl, Chirality-induced polarization effects in the cuticle of scarab beetles: 100 years after Michelson, Philosophical Magazine 92, 2012-04-21, עמ' 1583–1599 doi: 10.1080/14786435.2011.648228
  27. ↑ רמי אריאלי, משקפי שמש בנהיגה - לייזרים ויישומיהם, באתר לייזרים ויישומיהם - מכון ויצמן, ‏4 בדצמבר 2016
  28. ↑ What Is an LCD Polarizer? -, Nelson Miller Group, ‏15 ביולי 2020
  29. ↑ Larissa Vertchenko, Lev Vertchenko, Verification of Malus's Law using a LCD monitor and Digital Photography, www.scielo.br, ‏2016 (בפורטוגזית ואנגלית)
  30. ↑ רמי אריאלי, חלונות קצה בלייזר גזי - לייזרים ויישומיהם, באתר לייזרים ויישומיהם - מכון ויצמן, ‏4 בדצמבר 2016
  31. ^ 31.0 31.1 Basics of Polarizing Microscopy, research.physics.berkeley.edu, Olympus
  32. ^ 32.0 32.1 27.8: Polarization, Physics LibreTexts, ‏2016-07-24 (באנגלית)
  33. ↑ רמי אריאלי, בצילום - לייזרים ויישומיהם, באתר מכון ויצמן למדע, ‏2016-12-04
  34. ↑ Camera Polarizer Lens - Polarizing Filters | B&H Photo, www.bhphotovideo.com (באנגלית)
  35. ^ 35.0 35.1 Natural Resources Canada, Radar Polarimetry, natural-resources.canada.ca, ‏2008-01-28
  36. ↑ RAVEN Surface Ship Electronic Countermeasures System, lockheedmartin.com
  37. ↑ Q156 Series Polarizing Grids | L3Harris® Fast. Forward., www.l3harris.com
  38. ^ 38.0 38.1 J. Microw, Polarization Diversity on ESM Systems, www.scielo.br, ‏2017 (בפורטוגזית)
  39. ↑ Elane Chincheck, Radar Antenna Characterization Using Polarization Measurements, apps.dtic.mil, Naval Research Laboratory, ‏8 באוגוסט 1994
  40. ↑ “עיט הסלע”, באתר רפאל

מקטב42235796Q11942175

אוחזר מתוך "https://he.hamichlol.org.il/w/index.php?title=מקטב&oldid=3584792"