חוק הכבידה העולמי של ניוטון

F הוא כוח המשיכה, G הוא קבוע הכבידה, M היא המסה של כל אחד מהגופים, R הוא המרחק בין מרכזי הכובד

חוק הכבידה האוניברסלית של ניוטון הוא חוק פיזיקלי בסיסי של המכניקה הקלאסית, הקובע שכל חלקיק מושך כל חלקיק אחר ביקום בכוח שגודלו נקבע ביחס ישר למכפלת המסות שלהם וביחס הפוך לריבוע המרחק בין מרכזיהם. פרסום תיאוריה זו נודע כ"האיחוד הגדול הראשון", שכן הוא איחד את תופעות הכבידה שתוארו קודם לכן על כדור הארץ עם התנהגויות אסטרונומיות ידועות אחרות.

בשפה של היום, החוק קובע שכל מסה נקודתית מושכת כל מסה נקודתית אחרת על ידי כוח הפועל לאורך הקו החותך את שתי הנקודות. הכוח הוא יחסי למכפלה של שתי המסות, וכן נמצא ביחס ריבועי הפוך למרחק ביניהם.

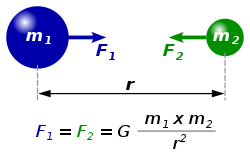
המשוואה עבור כוח הכבידה האוניברסלית מקבלת אפוא את הצורה:

$F=G{\frac {m_{1}m_{2}}{r^{2}}},$

כאשר F הוא כוח הכבידה הפועל בין שני עצמים, m₁ ו-m₂ הם המסות של העצמים, r הוא המרחק בין מרכזי המסות שלהם, ו-G הוא קבוע הכבידה.

חוק הכבידה של ניוטון דומה לחוק הכוחות החשמליים של שארל-אוגוסטן דה קולון – חוק קולון, המשמש לחישוב גודל הכוח החשמלי הנוצר בין שני גופים טעונים. שניהם חוקי ריבוע הפוך, כאשר הכוח הוא ביחס הפוך לריבוע המרחק בין הגופים. בחוק קולון ישנה מכפלה של שני מטענים במקום מכפלת המסות, ושימוש בקבוע קולון במקום בקבוע הכבידה. בעקבות הדמיון ביניהם הוגדר מושג חדש כדי לתאר את התופעה – כוח מרכזי.

החוק הוא חוק פיזיקלי כללי הנגזר מתצפיות אמפיריות – מה שאייזק ניוטון כינה "חשיבה אינדוקטיבית". החוק הוא חלק מהמכניקה הקלאסית והוא נוסח בספרו של ניוטון עקרונות מתמטיים של פילוסופיית הטבע ("הפרינקיפיה"), שפורסם לראשונה ב-5 ביולי 1687. כאשר ניוטון הציג את הכרך הראשון של הטקסט בפני החברה המלכותית, לפני שהוא פורסם, באפריל 1686, רוברט הוק טען שניוטון השיג ממנו את חוק הריבוע ההפוך.

המבחן הראשון של תיאוריה זו של ניוטון לגבי כוח בין מסות במעבדה היה ניסוי קוונדיש שערך המדען הבריטי הנרי קוונדיש בשנת 1798. ניסוי זה התרחש 111 שנים לאחר פרסום הספר הפרינקיפיה של ניוטון וכ-71 שנים לאחר מותו.

חוק ניוטון הוחלף מאז על ידי תורת היחסות הכללית של אלברט איינשטיין, אך הוא ממשיך לשמש כקירוב מצוין להשפעות הכבידה ברוב היישומים. תורת היחסות נדרשת רק כאשר יש צורך בדיוק קיצוני, או כאשר מתמודדים עם שדות כבידה חזקים מאוד, כמו אלו שנמצאו ליד עצמים מסיביים וצפופים במיוחד, או במרחקים קטנים (כגון מסלולו של כוכב חמה סביב השמש).

היסטוריה

לפני ניוטון

השערות בדבר קשרים ריבועיים בטבע הוצעו אף לפני תקופתו של ניוטון.

בשנת 1604, גלילאו גליליי שיער נכונה שהמרחק שעצם עובר בזמן שהוא נופל – פרופורציונלי לריבוע הזמן שחלף באותה נפילה. קשר זה, בין המרחק שעצמים עוברים בנפילה חופשית לבין ריבוע הזמן, אושר על ידי הישועים האיטלקיים גרימלדי וריציולי בין השנים 1640 ל-1650. הם גם ערכו חישוב של עוצמת כוח המשיכה של כדור הארץ על ידי רישום התנודות של מטוטלת.

הערכה מודרנית לגבי ההיסטוריה המוקדמת של חוק הריבועים ההפוכים היא שעד סוף שנות ה-70 של המאה ה-17, ההנחה של "יחס הפוך בין כוח המשיכה לריבוע המרחק הייתה נפוצה למדי וקודמה על ידי מספר אנשים שונים עבור סיבות שונות". אותו מחבר זוקף לזכותו של רוברט הוק תרומה משמעותית ומכריעה לחוק, אך מתייחס לטענה של הוק בדבר גילוי חוק הריבוע ההפוך כלא רלוונטית, שכן מספר אנשים מלבד ניוטון והוק הציעו זאת. במקום זאת, הוא מצביע על הרעיון של "צירוף התנועות השמיימיות" (כלומר שילוב התנועה המשיקית והרדיאלית בתנועה מעגלית), והמרת החשיבה של ניוטון מכוח צנטריפוגלי לכיוון כוח צנטריפטלי כתרומה המשמעותית של הוק.

בשנת 1687 פרסם ניוטון את ספרו עקרונות מתמטיים של פילוסופיית הטבע ("הפרינקיפיה"), בו הציג את חוקי התנועה שלו ואת חוק הכבידה האוניברסלי.

בספרו נתן ניוטון קרדיט לשני אנשים: לבוליאדיאוס (שכתב ללא הוכחה שיש כוח על כדור הארץ שמצביע לכיוון השמש), ולבורלי (שכתב שכל כוכבי הלכת נמשכים לשמש). ייתכן שההשפעה העיקרית הייתה בורלי, שלניוטון היה עותק של ספרו.

הוויכוח על גניבה ספרותית

בשנת 1686, כאשר הוצג הספר של ניוטון, הפרינקיפיה, בפני החברה המלכותית הבריטית, רוברט הוק האשים את ניוטון בגנבה ספרותית בטענה שהוא לקח ממנו את הרעיון של "חוק הפחתת כוח המשיכה, בהיותו הופכי לפי ריבועי המרחקים מהמרכז". אם כי במקביל (לפי הדו"ח של אדמונד האלי מאותה תקופה) הוק הסכים ש"הדגמת העקומות שנוצרות על ידי כך" היא לגמרי של ניוטון.

עבודתו ותביעותיו של הוק נגד ניוטון

רוברט הוק פרסם את רעיונותיו על "מערכת העולם" (System of the World) בשנות ה-60 של המאה ה-17, במסגרת הרצאה שנתן לחברה המלכותית הבריטית ב-21 במרץ 1666, שם קרא מאמר "הנוגע להטייה של תנועה ישירה לתנועה עקומה בשל עיקרון משיכה פנימה".

הוק פרסם רעיונות אלה שוב בצורה מפותחת ב-1674, כתוספת ל"ניסיון להוכיח את תנועת כדור הארץ מתצפיות". הוק הכריז באותה שנה כי הוא מתכנן "להסביר מערכת עולם השונה בפרטים רבים מכל אחת שידועה עד כה", בהתבסס על שלוש הנחות:

1. ש"לכל הגופים השמימיים באשר הם, יש משיכה או כוח משיכה למרכזים שלהם" ו"הם גם מושכים את כל שאר הגופים השמימיים שנמצאים בתחום פעילותם";
2. ש"כל הגופים באשר הם שמוכנסים לתנועה ישירה ופשוטה, ימשיכו לנוע קדימה בקו ישר, עד שהם יוסטו ויוכפפו על ידי כמה כוחות אפקטיביים..." (החוק הראשון של ניוטון)
3. "כוחות המשיכה הללו הם חזקים יותר בפעולה שלהם, ככל שהגוף הנמשך יותר קרוב למרכזים שלהם".

לפיכך הניח הוק משיכה הדדית בין השמש לכוכבי הלכת, באופן שגדל עם הקרבה לגוף המושך, יחד עם עיקרון של אינרציה ליניארית.

עם זאת, הצהרותיו של הוק עד 1674 לא הזכירו, שחוק ריבוע הפוך חל או עשוי לחול על משיכות אלו. גם הכבידה של הוק עדיין לא הייתה אוניברסלית, אם כי היא התקרבה לאוניברסליות קרוב יותר מהשערות קודמות. הוא גם לא סיפק ראיות נלוות או הדגמה מתמטית לטענות שלו. על שני ההיבטים האחרונים, הוק עצמו הצהיר ב-1674: "עכשיו מהן למעשה דרגות [של משיכה] אלה, טרם אימתתי בניסוי"; ולגבי כל הצעתו: "זאת אני רק רומז כרגע", "יש לי ביד דברים רבים אחרים שהייתי משלים תחילה, ולכן לא יכול כל כך להשתתף בה" (כלומר "להעמיד לדין את החקירה הזו").

רק מאוחר יותר, במכתב מ-6 בינואר 1679 לניוטון, הוק ביטא את חשדו "שהמשיכה תמיד נמצאת בפרופורציה ריבועית למרחק מהמרכז, וכתוצאה מכך המהירות תהיה בפרופורציה שורשית למשיכה, ולכן, כפי שקפלר מניח, הופכית למרחק." (המסקנה לגבי המהירות הייתה שגויה.)

התכתבות זו של הוק עם ניוטון בשנים 1679–1680 לא רק הזכירה את ההנחה הריבועית ההפוכה הזו לירידה במשיכה עם הגדלת המרחק, אלא גם, במכתב הפתיחה של הוק לניוטון, מ-24 בנובמבר 1679, הזכירה את הגישה של "צירוף תנועות של כוכבי הלכת השמימיים: תנועה ישירה לאורך המשיק ותנועה מושכת לכיוון הגוף המרכזי".

עבודתו וטענותיו של ניוטון נגד הוק

ניוטון, כאשר התמודד במאי 1686 עם טענתו של הוק על חוק הריבוע ההפוך, הכחיש כי הקרדיט לחיבור הרעיון מגיע להוק. בין הסיבות, ניוטון נזכר שהרעיון נדון עם סר כריסטופר רן לפני מכתבו של הוק מ-1679. ניוטון גם הצביע והכיר בעבודה קודמת של אחרים, כולל בוליאלדוס, (שהציע, אך ללא הדגמה, שיש כוח משיכה מהשמש ביחס ריבועי ההפוך למרחק), ובורלי (שהציע, גם ללא הדגמה, שקיימת נטייה צנטריפוגלית המאזנת את המשיכה לכיוון השמש, וגורמת לכוכבי הלכת לנוע באליפסות). ההיסטריון טום וייטסייד גם כן תיאר את התרומה למחשבה של ניוטון, שהגיעה מספרו של בורלי – שעותק שלו היה בספרייתו של ניוטון במותו.

ניוטון עוד הגן על עבודתו באומרו שאפילו אם היה שומע לראשונה על הפרופורציה הריבועית ההפוכה מהוק, עדיין היו לו כמה זכויות עליה בשל הדגמות הדיוק שלו. הוק, ללא ראיות בעד השערה זו, יכול היה רק לנחש שחוק הריבוע ההפוך תקף בקירוב במרחקים גדולים מהמרכז. לטענת ניוטון, בזמן שספרו, עקרונות מתמטיים של פילוסופיית הטבע, עדיין היה בשלב טרום-הפרסום, היו כל כך הרבה סיבות אפשריות לפקפק בדייקנותו של חוק הריבוע ההפוך (במיוחד קרוב לתחום המושך) כך ש"ללא ההדגמות שלי (כלומר של ניוטון), שמר הוק עדיין היה זר להן, לא היה אפשרי להאמין לפילוסוף נבון שהוא מדויק בשום צורה."

הערה זו לגבי ה'הדגמות' של ניוטון מתייחסת בין היתר לממצא של ניוטון, הנתמך בהדגמה מתמטית, שאם חוק הריבוע ההפוך חל על חלקיקים זעירים, אז אפילו מסה סימטרית כדורית גדולה מושכת מסות חיצוניות לפני השטח שלה – בדיוק כאילו כל המסה שלה מרוכזת במרכזה. לפיכך נתן ניוטון הצדקה, שאחרת הייתה חסרה, להחלת חוק הריבוע ההפוך על מסות פלנטריות כדוריות גדולות כאילו היו חלקיקים זעירים. בנוסף, ניוטון ניסח, בטענות 43–45 של כרך 1 ובסעיפים הקשורים בכרך 3, מבחן רגיש לבחינת הדיוק של חוק הריבוע ההפוך, שבו הראה שרק במקרה שבו מחושב חוק הכוח כריבוע ההפוך של המרחק, המסלול האליפיטי של כוכבי הלכת יישאר קבוע כפי שהוא נצפה (מלבד השפעות קטנות המיוחסות להפרעות בין-כוכביות).

בהתייחס לראיות שעדיין שרדו מההיסטוריה המוקדמת יותר, כתבי יד שכתב ניוטון בשנות ה-60 של המאה ה-17 מראים שניוטון עצמו, עד 1669, הגיע להוכחות שבמקרה מעגלי של תנועה פלנטרית, דווקא לכוח הצנטריפוגלי היה יחס ריבועי הפוך עם המרחק מהמרכז. רק לאחר ההתכתבות שלו עם הוק בשנים 1679–1680, אימץ ניוטון את שפת הכוח הפנימי או הצנטריפטלי. לפי חוקר ניוטון ג'יי ברוס ברקנרידג', אף על פי שנעשו מאז הרבה שינויים בשפה ובנקודת המבט, כמו בין כוחות צנטריפוגליים וצנטריפטליים, החישובים וההוכחות בפועל נשארו זהים בכל מקרה. החישובים כללו גם את השילוב של תזוזות משיקיות ורדיאליות, שניוטון ביצע בשנות ה-60 של המאה ה-17. השיעור שהציע הוק לניוטון כאן, אף על פי שהוא משמעותי, היה רק של פרספקטיבה ולא שינה את הניתוח. רקע זה מראה שהיה בסיס לניוטון להכחיש את אימוץ חוק הריבוע ההפוך מהוק.

ההכרה של ניוטון

מהצד השני, ניוטון אכן קיבל והודה, בכל המהדורות של הפרינקיפיה, כי הוק (אך לא רק הוק) העריך בנפרד את חוק הריבוע ההפוך במערכת השמש; ניוטון הודה לרן, הוק והאלי בהקשר זה בהערה לטענה 4 בספר 1. ניוטון גם הודה בפני האלי שההתכתבות שלו עם הוק בשנים 1679–1680 עוררה מחדש את העניין הרדום שלו בעניינים אסטרונומיים, אבל זה לא אומר, לפי ניוטון, שהוק גילה לניוטון משהו חדש או מקורי: "בכל זאת אני לא חייב לו על שפיכת כל אור לתוך העסק הזה, אלא רק על ההסחה שהוא נתן לי ממחקרים אחרים שלי לחשוב על הדברים האלה ועל הדוגמטיות (כלומר הנחרצות) שלו בכתיבה כאילו גילה את התנועה באליפסה, שהובילה אותי לנסות אותה..."

מחלוקות מודרניות

מאז זמנם של ניוטון והוק, דיונים מודרניים נגעו גם בשאלה האם האזכור של הוק משנת 1679 של 'צירוף התנועות' (כלומר התנועה המשיקית והרדיאלית בתנועה מעגלית) סיפק לניוטון משהו חדש ובעל ערך, אף על פי שזו לא הייתה טענה שהושמעה בפועל על ידי הוק באותה תקופה. כפי שתואר לעיל, כתבי היד של ניוטון משנות ה-60 של המאה ה-17 מראים אותו למעשה משלב תנועה משיקית עם השפעות של כוח מכיוון רדיאלי, למשל בגזירתו של היחס הריבועי ההפוך עבור המקרה המעגלי. הכתבים גם מראים שניוטון מבטא בבירור את המושג של אינרציה ליניארית – שבגינו היה חייב לעבודתו של דקארט, שפורסמה ב-1644 (כפי שהיה כנראה הוק חייב). נראה שהעניינים הללו לא נלמדו על ידי ניוטון מהוק.

עם זאת, למספר סופרים היה עוד מה לומר על מה שניוטון הרוויח מהוק וכמה היבטים נותרו שנויים במחלוקת. העובדה שרוב המסמכים הפרטיים של הוק הושמדו או נעלמו לא עזרה לבסס את האמת.

תפקידו של ניוטון בנוגע לחוק הריבוע ההפוך לא היה כפי שהוא מוצג לפעמים. הוא לא התיימר לחשוב על זה כרעיון בלבד. מה שניוטון עשה, למעשה, היה להראות כיצד לחוק המשיכה של הריבועים ההפוכים היו קשרים מתמטיים הכרחיים רבים עם תכונות נצפות של תנועות הגופים במערכת השמש; ושהם היו קשורים בצורה כזו שהראיות התצפיתניות וההדגמות המתמטיות, ביחד, נתנו סיבה להאמין שחוק הריבוע ההפוך לא רק נכון בערך אלא נכון בדיוק (ברמת הדיוק שניתן היה להשיג בתקופתו של ניוטון ובמשך בערך מאתיים שנים לאחר מכן – ועם כמה נקודות שעדיין לא ניתן היה לבחון בוודאות, שבהן ההשלכות של התיאוריה עדיין לא זוהו או חושבו בצורה מספקת).

כשלושים שנה לאחר מותו של ניוטון ב-1727, כתב אלכסיס קלייראוט, אסטרונום מתמטי בולט בזכות עצמו בתחום חקר הכבידה, לאחר שסקר את מה שפרסם הוק, כי "אסור לחשוב שהרעיון הזה... של הוק מפחית את התפארת של ניוטון"; וכי "הדוגמה של הוק" משרתת "להראות איזה מרחק יש בין אמת נראית לבין אמת מוכחת".

ההסתייגות של ניוטון לגבי כוח הכבידה

בעוד שניוטון הצליח לנסח את חוק הכבידה שלו ביצירתו המונומנטלית, הוא חש אי נוחות עמוקה מהמושג "פעולה מרחוק" שהמשוואות שלו מרמזות עליו. בשנת 1692, במכתבו השלישי לבנטלי, הוא כתב:

"[הרעיון] שגוף אחד יכול לפעול על רעהו, מרחוק, דרך ואקום וללא תיווך של שום דבר אחר, [...], הוא בעיני אבסורד כה גדול, שלדעתי, אף אדם שיש לו במובנים פילוסופיים סגל חשיבה מוכשר לא יוכל ליפול לתוכו".

— אייזיק ניוטון

ניוטון מעולם לא, במילותיו, "נתן את הסיבה לכוח הזה". בכל שאר המקרים שאינם כבידה, הוא השתמש בתופעת התנועה כדי להסביר את מקורם של כוחות שונים הפועלים על גופים, אך במקרה של כוח הכבידה, הוא לא הצליח לזהות בניסוי את התנועה המייצרת את כוח הכבידה (אף על פי שהוא המציא שתי השערות מכניות ב-1675 וב-1717). יתרה מכך, הוא סירב אפילו להציע השערה באשר לגורם לכוח זה בטענה שהדבר מנוגד למדע הגיוני. הוא צר על כך ש"פילוסופים ניסו עד עתה לשווא לחפש בטבע" אחר מקור כוח הכבידה, שכן הוא שוכנע "מסיבות רבות" שישנן "סיבות שלא היו ידועות עד כה" שהן יסוד לכל "תופעות הטבע". תופעות יסוד אלו עדיין נמצאות בחקירה, ואף על פי שיש השערות רבות, עדיין לא נמצאה התשובה הסופית.

בסכוליום הכללי של ניוטון משנת 1713 במהדורה השנייה של הפרינקיפיה הוא כתב: "עדיין לא הצלחתי לגלות את הגורם לתכונות הכבידה הללו מתוך תופעות ואיני בודה השערות ... די בכך שכוח הכבידה אכן קיים ופועל על פי החוקים שהסברתי, ושהוא מצליח בשפע להסביר את כל התנועות של גרמי השמים".

אחרים מתחו ביקורת על ניוטון בנקודה זו. למשל, לייבניץ:

אין זה די לומר "חוק האלוקים הוא זה" ובכך להצדיק את פעולת הטבע. על החוק להסביר את טבעם של דברים. כך, למשל, אם היה הקל בורא את העולם כך שהגופים בו היו כולם נעים מסביב למרכז מסוים, הרי שהיה עליו להצמידם לגופים אחרים הנעים בתנועה מעגלית או להצמיד מלאך אל חישוקיהם, שאחרת היה יוצר חריגות בתנועתם.

— גוטפריד וילהלם לייבניץ

צורה מודרנית

תרשים של שתי מסות המושכות זו את זו

בשפה מודרנית, החוק קובע שכל מסה נקודתית מושכת כל מסה נקודתית אחרת על ידי כוח הפועל לאורך הקו החותך את שתי הנקודות. הכוח הוא יחסי למכפלה של שתי המסות ועומד ביחס הפוך לריבוע המרחק ביניהם:

$F=G{\frac {m_{1}m_{2}}{r^{2}}}\$

כאשר:

• F הוא הכוח בין המסות;
• G הוא קבוע הכבידה, קבוע אוניברסלי המגדיר את היחס בין שני הביטויים;
• m₁ היא המסה הראשונה;
• m₂ היא המסה השנייה;
• r הוא המרחק בין מרכזי המסות.

השוואת תוצאות ניסויים שונים עבור ערכו המספרי של G; הקו המרכזי (בשחור) מסמן את ערך G המומלץ והמעודכן. הרצועה (באפור) מסמנת את טווח השגיאה עבור ערך זה

ביחידות SI, הכוח F נמדד ביחידות ניוטון (N), המסות בקילוגרמים (ק"ג), המרחק r במטרים (m), והקבוע G שווה ל: $G=6.67384\times 10^{-11}{m^{3} \over s^{2}kg}$

ערכו של הקבוע G נקבע לראשונה במדויק מתוצאות ניסוי קוונדיש שערך המדען הבריטי הנרי קוונדיש ב-1798, אם כי קוונדיש לא חישב בעצמו ערך מספרי עבור G. ניסוי זה היה גם המבחן הראשון של תורת הכבידה של ניוטון במעבדה. ניסוי זה התרחש 111 שנים לאחר פרסום הפרינקיפיה של ניוטון ו-71 שנים לאחר מותו של ניוטון, כך שאף אחד מהחישובים של ניוטון לא יכול היה להשתמש בערך המספרי של G; במקום זאת הוא יכול היה רק לחשב כוח ביחס לכוח אחר.

גופים בעלי היקף מרחבי

ערך מורחב – משפט הקליפה

חוזק שדה הכבידה בתוך כדור הארץ

שדה הכבידה ליד פני כדור הארץ – אובייקט מוצג בהאצה לעבר פני השטח

אם לגופים המדוברים יש היקף מרחבי (בניגוד לגופים שהם מסות נקודתיות), אזי כוח הכבידה ביניהם מחושב על ידי סיכום הכוח הנוצר מכל הנקודות המרכיבות את הגופים. ככל שהנקודות המרכיבות את הגופים הופכות ל"קטנות לאין שיעור", הדבר כרוך בביצוע אינטגרל על הכוח (בצורה וקטורית, ראה להלן) על פני נפחם הכולל של שני הגופים.

בדרך זו ניתן להראות שעצם בעל התפלגות מסה סימטרית כדורית מפעיל את אותה משיכה כבידתית על גופים חיצוניים כאילו כל מסת העצם מרוכזת בנקודה במרכזו. (אף שזה לא נכון בדרך כלל עבור גופים לא סימטריים כדוריים)

עבור גוף שנקודותיו מתפלגות בסימטריה כדורית, ניתן להשתמש במשפט הקליפה של ניוטון כדי למצוא את כוח הכבידה. המשפט אומר לנו כיצד חלקים שונים של התפלגות המסה משפיעים על כוח הכבידה הנמדד בנקודה הממוקמת במרחק $r_{0}$ ממרכז התפלגות המסה:

• החלק של המסה שנמצא ברדיוס $r<r_{0}$ גורם לאותו כוח ברדיוס $r_{0}$ כאילו כל המסה הכלולה בתוך כדור ברדיוס $r_{0}$ הייתה מרוכזת במרכז התפלגות המסה (כפי שצוין לעיל).
• החלק של המסה שנמצא ברדיוס $r>r_{0}$ לא מפעיל כוח כבידה שקול ברדיוס $r_{0}$ מהמרכז. כלומר, כוחות הכבידה הבודדים המופעלים על נקודה ברדיוס $r_{0}$ על ידי יסודות המסה מחוץ לרדיוס $r_{0}$ מבטלים זה את זה.

כתוצאה מכך, למשל, בתוך קליפה כדורית בעלת עובי וצפיפות אחידים אין תאוצת כבידה נטו בשום מקום בתוך הכדור החלול.

שדה הכבידה המקיף את כדור הארץ מנקודת מבט מקרוסקופית.

צורה וקטורית

ניתן לכתוב את חוק הכבידה האוניברסלי של ניוטון כמשוואה וקטורית כדי להסביר את כיוון כוח הכבידה כמו גם את גודלו.

${\vec {F}}_{21}=-G{m_{1}m_{2} \over {\vert {\vec {r}}_{21}\vert }^{2}}\,{\hat {r}}_{21}$

כאשר

• ${\vec {F}}_{21}$ הוא הכוח המופעל על אובייקט 2 על ידי אובייקט 1,
• $G$ הוא קבוע הכבידה,
• $m_{1}$ ו-$m_{2}$ הם המסות של עצמים 1 ו-2 בהתאמה,
• $|{\vec {r}}_{21}|\ {\stackrel {\mathrm {def} }{=}}\ |{\vec {r}}_{2}-{\vec {r}}_{1}|$ הוא המרחק בין עצמים 1 ו-2,
• ${\hat {r}}_{21}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {{\vec {r}}_{2}-{\vec {r}}_{1}}{\vert {\vec {r}}_{2}-{\vec {r}}_{1}\vert }}$ הוא וקטור היחידה מאובייקט 1 לאובייקט 2.

ניתן לראות שהצורה הווקטורית של המשוואה זהה לצורה הסקלרית שניתנה קודם לכן, אלא שעכשיו $F$ הוא גודל וקטורי, והצד הימני מוכפל בווקטור היחידה המתאים, המייצג כיוון. כמו כן, ניתן לראות כי ${\vec {F}}_{12}=-{\vec {F}}_{21}$.

שדה כבידה

שדה כבידה הוא שדה וקטורי המתאר את כוח הכבידה שיופעל על עצם בכל נקודה נתונה במרחב, ליחידת מסה. גודל זה למעשה שווה לתאוצת הכובד באותה נקודה. זוהי הכללה של הצורה הווקטורית, שהופכת שימושית במיוחד אם מעורבים יותר משני עצמים (כגון רקטה בין כדור הארץ לירח).

עבור שני עצמים שאנו מתעניינים רק בתנועת העצם השני ביחס לכבידה שיוצר העצם הראשון (למשל, עצם 2 הוא רקטה, עצם 1 כדור הארץ), אנו פשוט כותבים ${\vec {r}}$ במקום ${\vec {r}}_{12}$ ו-$m$ במקום $m_{2}$ ומגדירים את שדה הכבידה ${\vec {g}}({\vec {r}})$ כ:

${\vec {g}}({\vec {r}})=-G{m_{1} \over {{\vert {\vec {r}}\vert }^{2}}}\,{\hat {r}}$

כדי שנוכל לכתוב:

${\vec {F}}({\vec {r}})=m{\vec {g}}({\vec {r}})$

הגדרת השדה תלויה אך ורק באובייקטים הגורמים לשדה. לשדה יש יחידות תאוצה; ב-SI, התאוצה נמדדת ביחידות של m/s².

שדות כבידה הם גם שדות ווקטוריים משמרים; כלומר, העבודה הנעשית על ידי כוח הכבידה מנקודה אחת לאחרת היא לא תלויה בנתיב. כתוצאה מכך, אפשר להגדיר פוטנציאל כבידתי $V({\vec {r}})$ כך ש:

${\vec {g}}({\vec {r}})=-{\vec {\nabla }}V({\vec {r}})$

אם $m_{1}$ היא מסה נקודתית או מסה של כדור עם צפיפות מסה אחידה, שדה הכוח ${\vec {g}}({\vec {r}})$ מחוץ לכדור הוא איזוטרופי, כלומר תלוי רק במרחק ${\vec {r}}$ ממרכז הכדור. במקרה הזה:

$V({\vec {r}})=-G{\frac {m_{1}}{|{\vec {r}}|}}.$

יהיה הפוטנציאל הכבידתי, בתוך ומחוץ למסות הסימטריות.

לפי חוק גאוס לכבידה אפשר גם למצוא את שדה הכבידה בגוף סימטרי, למשל:

עבור כדור חלול בעל רדיוס $R$ ומסה כוללת $M$,

$|{\vec {g}}(r)|={\begin{cases}0,&{\text{if }}r<R\\\\{\dfrac {GM}{r^{2}}},&{\text{if }}r\geq R\end{cases}}$

ועבור כדור מוצק אחיד בעל רדיוס $R$ ומסה כוללת $M$ ,

$|{\vec {g}}(r)|={\begin{cases}{\dfrac {GMr}{R^{3}}},&{\text{if }}r<R\\\\{\dfrac {GM}{r^{2}}},&{\text{if }}r\geq R\end{cases}}$

מגבלות

תיאור כוח המשיכה של ניוטון מדויק מספיק למטרות מעשיות רבות ולכן נעשה בו שימוש נרחב. הסטיות ממנו קטנות כאשר הגדלים $\phi /c^{2}$ ו $(v/c)^{2}$ שניהם קטנים הרבה יותר מאחד, כאשר $\phi$ הוא הפוטנציאל הכבידתי, $v$ היא המהירות של העצמים הנלמדים, ו-$c$ היא מהירות האור בוואקום. לדוגמה, כוח הכבידה הניוטוני מספק תיאור כמעט מדויק של מערכת כדור הארץ עם השמש, שכן

${\frac {\phi }{c^{2}}}={\frac {GM_{\mathrm {sun} }}{r_{\mathrm {orbit} }c^{2}}}\sim 10^{-8},\quad \left({\frac {v_{\mathrm {Earth} }}{c}}\right)^{2}=\left({\frac {2\pi r_{\mathrm {orbit} }}{(1\ \mathrm {yr} )c}}\right)^{2}\sim 10^{-8}$

כאשר $r_{\text{orbit}}$ הוא רדיוס מסלול כדור הארץ סביב השמש.

במצבים שבהם אחד מהפרמטרים (חסרי הממדים) הוא גדול, אז יש להשתמש בתורת היחסות הכללית כדי לתאר את המערכת בדיוק. תורת היחסות הכללית מצטמצמת לכוח הכבידה הניוטוני בגבול הפוטנציאל הכבידתי הקטן והמהירויות הנמוכות, לכן אומרים שחוק הכבידה של ניוטון הוא "גבול הכבידה הנמוך" של תורת היחסות הכללית.

תצפיות הנוגדות את הנוסחה של ניוטון

• התיאוריה של ניוטון אינה מסבירה במלואה את נקיפת הפריהליון של מסלולי כוכבי הלכת, במיוחד זו של כוכב חמה, שהתגלתה זמן רב לאחר חייו של ניוטון. קיים פער של 43 שניות קשת כל מאה שנים בין החישוב הניוטוני, הנובע רק מהאינטראקציות הכבידתיות משאר כוכבי הלכת, לבין הנקיפה הנצפית, שהתגלתה בטלסקופים מתקדמים במהלך המאה ה-19.
• הסטייה הזוויתית שנחזית עבור ההתעקמות של קרני האור על ידי כוח הכבידה, כאשר מחשבים אותה באמצעות התיאוריה של ניוטון, היא רק מחצית מהסטייה שנצפתה על ידי אסטרונומים.^{[דרוש מקור][מפני ש...]} חישובים באמצעות תורת היחסות הכללית מתאימים הרבה יותר לתצפיות האסטרונומיות.
• בגלקסיות ספירליות, נראה שהסיבוב של כוכבים סביב מרכזם אינו מציית הן לחוק הכבידה האוניברסלי של ניוטון והן לתורת היחסות הכללית. אסטרופיזיקאים מסבירים את התופעה הבולטת הזו על ידי הנחת נוכחות של כמויות גדולות של חומר אפל. בעיה זו ידועה כבעיית המסה החסרה.

הפתרון של איינשטיין

שתי הסתירות הראשונות עם התצפיות לעיל הוסברו על ידי תורת היחסות הכללית של איינשטיין, שבה הכבידה היא ביטוי של מרחב-זמן עקום, במקום להיות תוצאה של כוח המתפשט בין גופים.

בתיאוריה של איינשטיין, אנרגיה ותנע מעוותים את המרחב-זמן בסביבתם, וחלקיקים אחרים נעים במסלולים שנקבעים על-ידי הגאומטריה של המרחב-זמן. תיאוריה זו אפשרה תיאור של תנועות האור והמסה שעולה בקנה אחד עם כל התצפיות הזמינות. בתורת היחסות הכללית, כוח הכבידה הוא כוח מדומה הנובע מהעקמומיות של המרחב-זמן, מכיוון שתאוצת הכובד של גוף בנפילה חופשית נובעת מכך שקו העולם שלו הוא גיאודזה של המרחב-זמן.

ניתוח תנועה של יותר משני גופים

ערך מורחב – בעיית שלושת הגופים
 

בעיית n הגופים היא בעיה קלאסית עתיקה המנסה לחזות את התנועות של קבוצה של גרמים שמימיים המקיימים אינטראקציה זה עם זה בכבידה. פתרון בעיה זו – מימי היוונים ואילך – הונע מהרצון להבין את תנועות השמש, כוכבי הלכת והכוכבים הגלויים. במאה ה-20, הבנת הדינמיקה של מערכות צבירים כדוריים הפכה לבעיה חשובה של n-גופים. בעיית n-הגופים בתורת היחסות הכללית קשה הרבה יותר לפתרון.

ניתן לנסח את הבעיה הפיזיקלית הקלאסית הזו באופן בלתי פורמלי כך: בהינתן תכונות המסלול הפסאודו-יציבות (מיקום מיידי, מהירות וזמן) של קבוצה של גרמי שמים, יש לחזות את הכוחות האינטראקטיביים ביניהם; וכתוצאה מכך, לחזות את תנועות המסלול האמיתיות שלהם לכל הזמנים העתידיים.

בעיית שני הגופים נפתרה לחלוטין, וגם בעיית שלושת הגופים, בצורה מוגבלת. לבעיה הכללית לעומת זאת, אין פתרון אנליטי.

ראו גם

• פרדוקס בנטלי
• חוקי קפלר
• חוקי ניוטון
• חוק קולון
• חוק גאוס לכבידה

קישורים חיצוניים

מדיה וקבצים בנושא חוק הכבידה העולמי של ניוטון בוויקישיתוף

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

39001260חוק הכבידה העולמי של ניוטון