תרבוע (מתמטיקה)

במתמטיקה, תרבוע (אנגלית: Quadrature) הוא מונח היסטורי שפירושו קביעת השטח של צורה מסוימת. נושא התרבוע שימש כאחד המקורות העיקריים לבעיות שהתניעו את פיתוח החשבון האינפיניטסימלי, והציג מושגים חשובים באנליזה מתמטית.

היסטוריה

שיטה עתיקה לקביעת הממוצע הגאומטרי של $a,b$

מתמטיקאים ביוון העתיקה, בהתאם לדוקטרינה הפיתגוראית, הבינו את המושג של קביעת שטחה של צורה כתהליך של בניית ריבוע ששטחו זהה לשטח הצורה (ומכאן מגיע המונח: "תרבוע"). הגאומטריקאים היוונים לא הצליחו תמיד במשימה (ראו תרבוע העיגול), אולם הם אכן הצליחו לרבע מספר צורות אשר "צלעותיהן" לא היו פשוט קטעים ישרים, כמו למשל את הסהרונים של היפוקרטס ואת הפרבולה (ראו תרבוע הפרבולה). בהתאם למסורת היוונית, בניות אלו חייבות היו להתבצע רק בעזרת סרגל ומחוגה.

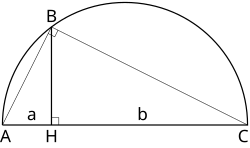
לצורך ביצוע תרבוע של מלבן שצלעותיו $a,b$ יש לבנות ריבוע שצלעו $x={\sqrt {ab}}$ (הממוצע הגאומטרי של $a,b$). למטרה זאת ניתן להשתמש בבנייה הבאה:

אם מציירים את המעגל שקוטרו נוצר על ידי חיבור שני קטעים ישרים באורך $a,b$ , אז הגובה ($BH$ בדיאגרמה) של הקטע הישר המאונך לקוטר, מנקודת החיבור של הקטעים עד לנקודה בה הוא חותך את המעגל, שווה לממוצע הגאומטרי של $a,b$ . בנייה גאומטרית דומה פותרת את הבעיות של תרבוע המקבילית והמשולש.

השטח של מקטע פרבולי הוא 4/3 השטח של משולש חסום מסוים

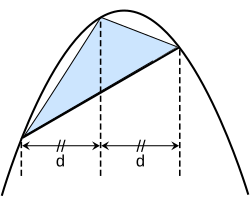
בעיות תרבוע של צורות עקמומיות היו קשות בהרבה. תרבוע העיגול בעזרת סרגל ומחוגה התברר במאה ה-19 כבלתי-אפשרי. אף על פי כן, עבור צורות מסוימות (למשל הסהרון של היפוקרטס) התרבוע ניתן לביצוע. התרבועים של פני השטח של הכדור ושל מקטע פרבולי על ידי ארכימדס הפכו להישג המתמטי הגבוה ביותר של האנליזה בעת העתיקה:

• שטח פני השטח של הכדור שווה לארבע פעמים השטח של מעגל גדול.
• שטחו של מקטע פרבולי שווה ל-${\tfrac {4}{3}}$ שטחו של משולש מסוים החסום במקטע הפרבולי.

כדי להוכיח את התוצאות הללו, ארכימדס השתמש בשיטת המיצוי של אאודוקסוס.

באירופה של ימי הביניים, המושג תרבוע קיבל משמעות של קביעת השטח של צורה בכל דרך שהיא. השיטה בה נעשה השימוש הרב ביותר היא שיטת הגדלים הבלתי-ניתנים לחלוקה; היא הייתה פחות ריגורוזית מאשר הבניות הגאומטריות של היוונים, אך פשוטה ויעילה יותר. באמצעותה, גלילאו גליליי וז'יל פרסון דה רוברוואל חישבו את השטח תחת קשת ציקלואידה, גרגואיר דה סנט וינסנט חקר את השטח תחת ההיפרבולה, ותלמידו Alphonse Antonio de Sarasa הבחין בקשר של השטח הזה ללוגריתמים.

ג'ון ואליס תרגם את השיטה הזאת לשפת האלגברה; הוא כתב בחיבורו Arithmetica Infinitorum (שפורסם בשנת 1656) מספר טורים שקולים למה שמכונה כיום האיטגרל המסוים, וחישב את הערכים שלהם. אייזק בארו וג'יימס גרגורי אף עשו התקדמות הלאה: הם חישבו תרבועים של כמה עקומים אלגבריים ושל ספירלות. כריסטיאן הויגנס ביצע בהצלחה תרבועים לשטחי הפנים של כמה גופי סיבוב.

תרבוע ההיפרבולה על ידי סנט וינסנט ו-de Sarasa הביא להגדרתה של פונקציה חדשה, הלוגריתם הטבעי, שהיא בעלת חשיבות יסודית. עם המצאת החשבון האינטגרלי נוצרה שיטה אוניברסלית לחישוב שטח. כתוצאה, המונח תרבוע הפך למסורתי (יש שיגידו ארכאי), ובמקומו המונח מציאת השטח הפך לשם הנפוץ יותר לבעיה המוגדרת כחישוב אינטגרל מסוים במשתנה אחד.

ראו גם

• תרבוע הפרבולה
• שיטות נומריות לחישוב אינטגרלים מסוימים