שרשרת פולימרית גאוסיאנית

שרשרת פולימרית גאוסיאנית (באנגלית: Gaussian Polymer Chain) הינה שרשרת בה אורך הווקטור המחבר בין מונומרים סמוכים מתפלג גאוסיאנית. פונקציית התפלגות ההסתברות של השרשרת כולה להיות בקונפורמציה מסוימת נקבעת על ידי מכפלת פונקציות ההתפלגות של כל וקטורי הקשר בשרשרת.
מודל השרשרת הגאוסיאנית מתאר את השרשרת הפולימרית כרצף של חלקיקים ספריים המחוברים ביניהם על ידי מוטות קשיחים או קפיצים. חיבורים אלו מכונים "וקטורי הקשר".

פולימר גמיש יכול להיות באחת מיני קונפורמציות רבות אפשריות. הקונפורמציה הינה הסידור המרחבי האפשרי של הפולימר הנקבע על ידי סט של $n$ וקטורי קשר המחברים אטומים שכנים.
הקונפורמציה הספיציפית של הפולימר נקבעת על ידי שלושה מאפיינים: גמישות השרשרת, אינטראקציות בין מונומרים על גבי השרשרת ואינטראקציות עם הסביבה. בין המונומרים לאורך השרשרת יכולות להיות אינטראקציות דוחות או מושכות. מספר הקונפורמציות האפשריות עבור פולימר גמיש הוא כה רב כך שמועיל יותר לתאר את צורת הפולימר באמצעות כלים סטטיסטים.

תיאור של שרשרת אידאלית. האטומים מיוצגים ככדורים (מסומנים באדום) והקשרים ביניהם מיוצגים על ידי מוטות קשיחים (מסומנים בכחול). הווקטור המצביע מאטום אחד לאטום שכן הינו "וקטור קשר" אשר לו הסתברות שווה להצביע לכל כיוון במרחב.

מודל השרשרת הגאוסיאנית נמצא בשימוש נרחב בתיאור קונפורמציות ותנועה של שרשראות בודדות באופן תאורטי. כמו כן, מודל זה יעיל בתיאור תנועה קולקטיבית של מערכות בהן יש שרשראות רבות.

מודלים לתיאור שרשראות פולימריות

מודלים עבור שרשראות פולימריות מתחלקים לשתי קבוצות: מודלים המתארים שרשראות אידאליות (Ideal chains) ומודלים המתארים שרשראות אמיתיות. שרשראות אידאליות הן שרשראות הממודלות תחת ההנחה כי בין המונומרים לא קיימת אינטראקציה בעוד שעבור שרשראות אמיתיות מתבצעת אינטראקציה בין המונומרים ובין השרשרת לבין התמיסה בה היא מצויה. חוזק אינטראקציה זו הוא שקובע האם באופן אפקטיבי קיימת דחייה או משיכה בין המונומרים.

וקטור קצה-קצה

וקטור קצה-קצה המחבר בין קצות הפולימר.

וקטור קצה-קצה ${\vec {R}}$ הינו הווקטור המחבר בין קצות הפולימר: הפענוח נכשל (שגיאת המרה. השרת ("https://wikimedia.org/api/rest_") השיב: "Cannot get mml. Server problem."): {\displaystyle {\vec {R}}=\sum _{i}^{N}{\vec {r}}_{i}} כאשר ${\vec {r}}_{i}$ הוא "וקטור הקשר" המחבר בין האטום ה- $i$ לאטום ה- $i+1$.

במקרה של שרשרת אידאלית מניחים שגודלו של וקטור הקשר קבוע: $|{\vec {r}}_{i}|=l$. לשרשראות שונות יהיו וקטורי קשר שונים ולכן וקטורי קצה-קצה שונים. המודל הכללי והפשוט ביותר של שרשרת אידאלית, Freely Joint Chain, מניח כי כל אחד מן הקשרים הינו בלתי תלוי בשכניו כך שיש לוקטור המתאר אותו הסתברות שווה להצביע לכל כיוון במרחב. תחת הנחה זו, משיקולי סימטריה מרחבית, מתחייב כי הממוצע על גבי הצבר (Ensemble average), שהינו הממוצע על גבי כל המצבים האפשריים של המערכת, מתאפס: $\langle {\vec {R}}\rangle =0$.

אולם, שורש ממוצע הריבועים ${\sqrt {\langle {\vec {R}}^{2}\rangle }}$ של וקטור הקצה-קצה אינו מתאפס:

$\langle {\vec {R}}^{2}\rangle =\langle \sum _{i=1}^{N}{\vec {r}}_{i}\sum _{j=1}^{N}{\vec {r}}_{j}\rangle =\sum _{i,j=1}^{N}\langle {\vec {r}}_{i}{\vec {r}}_{j}\rangle =l^{2}\langle cos\theta _{ij}\rangle$

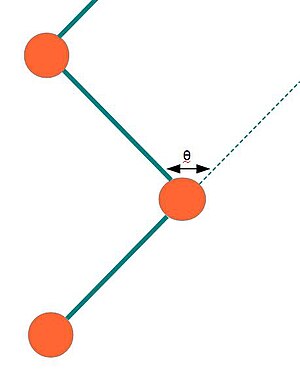
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{ij}} היא הזווית בין המונומר ה- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} למונומר ה-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} .

$\langle cos\theta _{ij}\rangle$ מחושב באופן שונה עבור כל אחד מן המודלים השונים המתארים שרשרשת אידאלית ולכן שורש ממוצע הריבועים מקבל ערך שונה עבור כל אחד ממודלים אלו.

פיתוח מתמטי של ההתפלגות הסטטיסטית של וקטור הקצה-קצה

ההסתברות של וקטור קצה-קצה של שרשרת פולימרית בעלת הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} קישוריות (וקטורי קשר) להיות באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} נתונה על ידי פונקציית התפלגות ההסתברות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\vec R,N)} :

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\vec R,N)=\int d\vec r_1 \int d\vec r_2 ...\int d\vec r_N \delta \left(\vec R - \sum_{n=1}^N r_n \right) \Psi({\vec r_n}) }

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ({\vec r_n})} הינה פונקציית ההתפלגות של פולימר להיות בקונפורמציה מסוימת. כיוון שווקטורי הקשר בלתי תלויים זה בזה, ניתן לכתוב את $\Psi ({{\vec {r}}_{n}})$ כמכפלה: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ({\vec r_n})= \prod_{n=1}^N \psi (\vec r_n)} . הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\vec r_n)} מבטא את גודלו הקבוע של וקטור הקשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec r_n} כך ש- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\vec r) = \frac {1}{4\pi l^2} \delta (|\vec r|-l)} תחת הנרמול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d \vec r \psi(\vec r) =1} .

על ידי שימוש בטרנספורם פורייה הפוך של פונקציית הדלתא של דיראק, ניתן לשכתב את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\vec R,N)} באופן הבא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\vec R,N)= \frac {1}{(2 \pi)^3} \int d \vec k e^{i \vec k \cdot \vec R} \int d \vec r_1 ... \int d \vec r_N \prod_{n=1}^N e^{-i \vec k \cdot \vec r_n} \psi (\vec r_n) = \frac {1}{(2\pi)^3} \int d \vec k e^{i \vec k \cdot \vec R} \left [\int d \vec r e^{-i \vec k \cdot \vec r} \psi (\vec r)\right ]^N }

ניתן לבחור את מערכת הצירים כך ש- ${\hat {k}}||{\hat {z}}$ ועל ידי בחירה זו מתקבל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d \vec r e^{-i \vec k \cdot \vec r} \psi (\vec r) = \frac {sin(kl)}{kl}}

עבור המקרה בו אנו דנים, כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N >> 1} , הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (\frac{sin(kl)}{kl} \right)^N \to 0} אלא אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle kl << 1} .

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle kl << 1} ניתן להשתמש בקירוב טיילור לקבלת:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (\frac{sin(kl)}{kl} \right)^N \approx \left (1- \frac {k^2l^2}{6}\right ) ^N \approx exp \left ({-\frac {Nk^2l^2}{6}}\right )}

כך ש- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi \left(\vec R,N \right ) = \frac {1}{(2\pi)^3} \int d \vec k e^{i \vec k \cdot \vec R} exp{\left(- \frac {Nk^2l^2}{6}\right)}} ועל ידי השלמה לריבוע האינטגרל על $k$ הופך לאינטגרל גאוסיאני פשוט שמניב את התוצאה:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi \left( \vec R, N \right) = \left( \frac{3}{2\pi N l^2} \right)^{3/2} exp{\left(-\frac{3R^2}{2Nl^2} \right)} }

כך שפונקציית ההתפלגות של וקטור הקצה-קצה היא גאוסיאן. אף על פי שתוצאה זו התקבלה עבור מודל Freely Joint Chain, היא תקפה עבור מקרה כללי יותר.

פונקציית התפלגות זו עלולה לתאר מצב לא פיזיקלי בו מתקיים שגודלו של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec R} גדול יותר מאורך השרשרת המקסימלי כאשר היא מתוחה לחלוטין, כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec R|>Nl} . כאשר עוסקים בתיאור פולימר על ידי המודלים הפיזיקליים הפשוטים ביותר, ניתן להניח כי הפולימר אינו במקסימום מתיחה אפשרית כך שזהו תיאור מספק.

באופן כללי, ניתן להראות כי מתקבלת תוצאה זהה עבור התפלגותו של וקטור הקצה-קצה בהינתן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ({\vec r_n})= \prod_{n=1}^N \psi (\vec r_n)} וכאשר השרשרת ארוכה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(N>>1\right )} . תוצאה זו מתקבלת על ידי משפט הגבול המרכזי.

מודל השרשרת הגאוסיאנית

שרשרת גאוסיאנית הינה שרשרת שאורך קשר שלה מתפלג גאוסיאנית: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\vec r) = \left( \frac{3}{2\pi b^2} \right)^{3/2} exp\left(-\frac{3r^2}{2b^2}\right)} כאשר $\langle r^{2}\rangle =b^{2}$.

באמצעות הכפלת ההתפלגויות של כל אחד מוקטורי הקשר ניתן לקבל את פונקציית התפלגות ההסתברות של הקונפורמציות של השרשרת כולה:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ({\vec r_n}) = \prod_{n=1}^N \left( \frac{3}{2\pi b^2} \right)^{3/2} exp\left(-\frac{3r_n^2}{2b^2}\right)}

שרשרת גאוסיאנית אינה מתארת באופן מדויק מבנה מקומי של פולימר אך מתארת היטב את תכונות הפולימר בסקאלת אורך גדולה. היתרון של מודל זה נובע מן הפשטות המתמטית המקלה על החישובים המתבצעים באמצעות המודל. שרשרת זו מתוארת לרוב על ידי מודל מכני בו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N+1} חרוזים מחוברים זה לזה באמצעות אוסצילטורים הרמוניים שהאנרגיה הפוטנציאלית של כל אחד מהם היא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_0 \left({\vec R_n}\right) = \frac {3}{2b^2}K_BT \sum_{n=1}^N \left( \vec R_n - \vec R_{n-1} \right)^2}

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_B} הינו קבוע בולצמן, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} הטמפרטורה ו- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\vec R_n} =\left (\vec R_0, ...,\vec R_N \right)} הם וקטורי המיקום של הקפיץ ה- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

בהקבלה לאנרגיה פוטנציאלית של אוסצילטור הרמוני פשוט הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (U_0 = \frac {1}{2} K \Delta x^2 \right )} ניתן לראות שקבוע הקפיץ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K = \frac {3K_BT}{b^2 }} .

ביביליוגרפיה

• M. Doi & S. F. Edwards,The Theory of Polymer Dynamics, New York: Oxford University Press, 1986

• M. Rubinstein & H. Colby,Polymer Physics, New York: Oxford University Press, 2003

• Paul J. Flory,Statistical Mechanics of Chain Molecules, Hanser Publishers

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0