צירוף ליניארי של אורביטלים אטומיים

שילוב ליניארי של אורביטלים אטומיים או (linear combination of atomic orbitals או LCAO) הוא תיאור לסופרפוזיציה קוונטית של אורביטלים אטומיים וטכניקה לחישוב אורביטלים מולקולריים בכימיה קוונטית. במכניקת הקוונטים, קונפיגורציות אלקטרונים של אטומים מתוארות כפונקציות גל. במובן מתמטי, פונקציות גל אלו הן פונקציות הבסיס המתארות את האלקטרונים של אטום נתון. בתגובות כימיות, פונקציות הגל האורביטליות משתנות, כלומר צורת ענן האלקטרונים משתנה, בהתאם לסוג האטומים המשתתפים בקשר הכימי והקשר הנוצר.

השיטה הוצגה בשנת 1929 על ידי סר ג'ון לנארד-ג'ונס ותיארה את הקשר במולקולות הדיאטומיות של השורה הראשית הראשונה של הטבלה המחזורית, אך שימשה קודם לכן את לינוס פאולינג לתיאור המולקולה הפשוטה ביותר הקיימת, H₂⁺ .

תיאור מתמטי

ההנחה vראשונית לצורך שימוש בשיטה היא שמספר האורביטלים המולקולריים שווה למספר האורביטלים האטומיים במערכת. במובן מסוים, n אורביטלים אטומיים נסכמים ליצירת n אורביטלים מולקולריים, אשר ניתן למספרם מ- i = 1 עד n, ושאינם בהכרח זהים. הביטוי עבור האורביטל המולקולרי ה- i יהיה:

${\varphi }_i=c_{1i}{\chi }_1+c_{2i}{\chi }_2+c_{3i}{\chi }_3+\cdots +c_{ni}{\chi }_n$

אוֹ

${\varphi }_i=\sum _r{c}_{ri}{\chi }_r$

כאשר ${\varphi }_i$ הוא האורביטל מולקולרי i המיוצג כסכום של n אורביטלים אטומיים ${\chi }_r$, כשכל אחד מהם מוכפל במקדם המתאים $c_{ri}$, ו- r (הממוספר מ-1 עד n ) מייצג איזה אורביטל אטומי נסכם. המקדמים הם משקלי התרומות של n האורביטלים האטומיים לאורביטל המולקולרי i. שיטת הרטרי-פוק משמשת כדי לקבל את ערכי המקדמים. האורביטלים מבוטאים, אם כן, כצירופים ליניאריים של פונקציות בסיס, כאשר פונקציות הבסיס הן פונקציות הגל של אלקטרון יחיד שעשויות להיות מרוכזות או לא להיות ממורכזות סביב גרעיני האטומים המרכיבים את המולקולה. פונקציות הבסיס מכונות בדרך כלל גם אורביטלים אטומיים (אם כי שם זה מתאים רק למקרה בו האלקטרונים ממורכזים סביב הגרעינים). האורביטלים האטומיים המשמשים הם בדרך כלל הם אלו של אטומים דמויי מימן היות שאלו ידועים אנליטית, כלומר אורביטלים מסוג סלייטר, אך ישנן גם אפשרויות אחרות כגון פונקציות גאוסיות מקבוצות בסיס סטנדרטיות.

דוגמה לדיאגרמת אורביטלים מולקולרית.

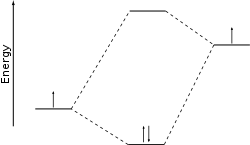
על ידי מינימיזציה של האנרגיה הכוללת של המערכת, נקבעים מקדמי הצירופים הליניאריים. גישה כמותית זו ידועה כיום כשיטת הרטרי-פוק. מאז התפתחות הכימיה החישובית, שיטת LCAO משמשת בעיקר לדיון איכותני, השימושי מאוד לחיזוי ורציונליזציה של תוצאות המתקבלות באמצעות שיטות חישוביות מודרניות ומדויקות יותר. במקרה זה, צורת האורביטלים המולקולריים והאנרגיות המתאימות להם מוסקות בקירוב מהשוואת האנרגיות של האורביטלים האטומיים של האטומים הבודדים (או שברי מולקולות) ויישום טכניקות חישוביות שונות. אנרגיות האורביטלים האטומיים הנדרשות לצורך החישוב מחושבות או מוסקות מניסויים.

החישוב נעזר בסימטריה של המולקולות והאורביטלים המעורבים בקשר, ולכן נקרא לפעמים שילוב ליניארי מותאם סימטריה (SALC). השלב הראשון בתהליך זה הוא מציאת חבורת הסימטריה של המולקולה. מספר הקשרים שאינם מוזזים בהפעלת פעולה מסוימת של החבורה קרוי אופי הפעולה. ייצוג זה מפורק לסכום של ייצוגים בלתי פריקים. ייצוגים אלו תואמים לסימטריה של האורביטלים המעורבים.

דיאגרמות אורביטליות מולקולריות מספקות טיפול LCAO איכותני פשוט. שיטת היקל, שיטת היקל המורחבת ושיטת פריזר-פאר-פופל, מספקות תוצאות מדויקות יותר.

ראו גם

• שיטת הרטרי-פוק
• קשירה הדוקה

קישורים חיצוניים

מדיה וקבצים בנושא צירוף ליניארי של אורביטלים אטומיים בוויקישיתוף

• קישור ל-LCAO @ chemistry.umeche.maine.edu, שיעור בנושא

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

צירוף ליניארי של אורביטלים אטומיים41637240Q900666