פונקציות טריגונומטריות הפוכות

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

במתמטיקה, הפונקציות הטריגונומטריות ההפוכות הן פונקציות המתקבלות על ידי הפיכת הפונקציות הטריגונומטריות היסודיות.

הפונקציות הטריגונומטריות אינן חד-חד ערכיות בתחום הגדרתן, לכן יש לצמצם את תחומן כדי להגדיר את הפונקציות ההפוכות.

תכונות יסודיות

	$\arcsin (x)$	$\arccos (x)$
הפונקציה ההפיכה של	$\sin (x)$ (סינוס)	$\cos (x)$ (קוסינוס)
דרך נוספת לרשום את הפונקציה	${\sin }^{-1}(x)$	${\cos }^{-1}(x)$
תחום הגדרה	$-1\le x\le 1$	$-1\le x\le 1$
תמונה	$-\frac{\pi }{2}\le f(x)\le +\frac{\pi }{2}$	$0\le f(x)\le \pi$
הכללה לכל הישר הממשי	sin y = x אם ורק אם y = arcsin x + 2kπ או y = π − arcsin x + 2kπ עבור שלם k כלשהו.	cos y = x אם ורק אם y = arccos x + 2kπ או y = 2π − arccos x + 2kπ עבור שלם k כלשהו.
מונוטוניות	מונוטונית עולה ממש	מונוטונית יורדת ממש
סימטריה	פונקציה אי-זוגית: $\arcsin (-x)=-\arcsin (x)$	$\arccos (x)=\pi -\arccos (-x)$
אסימפטוטות	אין	אין
שורשים	$x=0$	$x=1$
קיצון מקומי	Minimum $(-1|-\frac{\pi }{2})$ Maximum $(1|\frac{\pi }{2})$	Minimum $(1|0)$ Maximum $(-1|\pi )$
גרף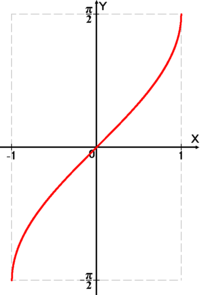
למידע נוסף	Arcsine, באתר MathWorld (באנגלית)	Arccosine, באתר MathWorld (באנגלית)

---

	$\arctan (x)$	$\mathrm{arccot}(x)$
הפונקציה ההפיכה של	$\tan (x)$ (טנגנס)	$\cot (x)$ (קוטנגנס)
דרך נוספת לרשום את הפונקציה	${\tan }^{-1}(x)$	${\cot }^{-1}(x)$
תחום הגדרה	$-\mathrm{\infty }<x<\mathrm{\infty }$	$-\mathrm{\infty }<x<\mathrm{\infty }$
תמונה	$-\frac{\pi }{2}<f(x)<\frac{\pi }{2}$	$0<f(x)<\pi$
הכללה לכל הישר הממשי	tan y = x אם ורק אם y = arctan x + kπ עבור שלם k כלשהו.	cot y = x אם ורק אם y = arccot x + kπ עבור שלם k כלשהו.
מונוטוניות	מונוטונית עולה ממש	מונוטונית יורדת ממש
סימטריה	פונקציה אי-זוגית: $\arctan (-x)=-\arctan (x)$	$\mathrm{arccot}(x)=\pi -\mathrm{arccot}(-x)$
אסימפטוטות	$f(x)\to \pm \frac{\pi }{2}$ כאשר $x\to \pm \mathrm{\infty }$	$f(x)\to \pi$ כאשר $x\to -\mathrm{\infty }$ $f(x)\to 0$ כאשר $x\to +\mathrm{\infty }$
שורשים	$x=0$	אין
קיצון מקומי	אין	אין
גרף
למידע נוסף	Arctangent, באתר MathWorld (באנגלית)	Arccotangent, באתר MathWorld (באנגלית)

---

	$\mathrm{arcsec}(x)$	$\mathrm{arccsc}(x)$
הפונקציה ההפיכה של	$\sec (x)$	$\csc (x)$
דרך נוספת לרשום את הפונקציה	${\sec }^{-1}(x)$	${\csc }^{-1}(x)$
תחום הגדרה	$-\mathrm{\infty }<x\le -1,1\le x<+\mathrm{\infty }$	$-\mathrm{\infty }<x\le -1,1\le x<+\mathrm{\infty }$
תמונה	$0\le f(x)<\frac{\pi }{2},\frac{\pi }{2}<f(x)\le \pi$	$-\frac{\pi }{2}\le f(x)<0,0<f(x)\le \frac{\pi }{2}$
הכללה לכל הישר הממשי	sec y = x אם ורק אם y = arcsec x + 2kπ או y = 2π − arcsec x + 2kπ עבור שלם k כלשהו.	csc y = x אם ורק אם y = arccsc x + 2kπ או y = π − arccsc x + 2kπ עבור שלם k כלשהו.
מונוטוניות	בכל אחד ממרכיבי תחום ההגדרה הפונקציה עולה ממש	בכל אחד ממרכיבי תחום ההגדרה הפונקציה יורדת ממש
סימטריה	$\mathrm{arcsec}(x)=\pi -\mathrm{arcsec}(-x)$	פונקציה אי-זוגית: $\mathrm{arccsc}(x)=-\mathrm{arccsc}(-x)$
אסימפטוטות	$f(x)\to \frac{\pi }{2}$ כאשר $x\to \pm \mathrm{\infty }$	$f(x)\to 0$ כאשר $x\to \pm \mathrm{\infty }$
שורשים	$x=1$	אין
קיצון מקומי	Minimum $(1|0)$ Maximum $(-1|\pi )$	Minimum $(-1|-\frac{\pi }{2})$ Maximum $(1|\frac{\pi }{2})$
גרף
למידע נוסף	Arcsecant, באתר MathWorld (באנגלית)	Arccosecant, באתר MathWorld (באנגלית)

קישורים חיצוניים

מדיה וקבצים בנושא פונקציות טריגונומטריות הפוכות בוויקישיתוף

• פונקציות טריגונומטריות הפוכות, באתר MathWorld (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

פונקציות טריגונומטריות הפוכות26545009