סוגריים
| סוגריים | ||||||
|---|---|---|---|---|---|---|
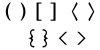
| ||||||
| סימני פיסוק | סימני כתב נוספים | |||||
|
נקודה . |
אמפרסנד (סימן "וגם") & | |||||
הסוגריים הם סימנים הבאים להפריד טקסט מסוים משאר הכתוב. ישנם שלושה סוגי סוגריים: רגילים – ( ), מרובעים – [ ], מסולסלים – { }, ויש גם המוסיפים עליהם את המְזֻוִּים – < >.
הסוגריים כסימן פיסוק
כשהם באים ברצף של כתוב, הסוגריים מופיעים משני צדדיה של הערה צדדית, אשר אינה קשורה במישרין לגוף הטקסט. כמו כן, בסוגריים לרוב רושמים מקור של ציטוט לאחר שהציטוט עצמו הובא.[1]
הראשונים לבוא הם הסוגריים הרגילים, בתוכם שמים (אם צריך) סוגריים מרובעים.[1]
בסוגריים מרובעים משתמשים כאשר בטקסט יש קטיעה של הרצף והטקסט מושלם על ידי העורך על סמך סברותיו או על סמך מחקרים. כמו כן, משתמשים בסוגריים מרובעים כאשר משלימים ציטוט, כדי לעשותו מובן יותר. לדוגמה: "[מדינת ישראל] תבטיח שוויון זכויות מדיני וחברתי גמור..." (מתוך הכרזת העצמאות).[1]
הסוגריים התפתחו מסימנים שהיו נהוגים בקרב סופרי העת העתיקה. ביוון היה זה הסיגמא (Σ) וה"אנטי־סיגמא" (סיגמא הפוכה) שסומנו בתחילת ובסוף טקסט כשרצו לציין שיש להשמיטו. סימן זה אף היה נהוג בקרב הסופרים העבריים של אותה תקופה, והוא נמצא מספר פעמים במגילות ים המלח שמקומראן. הסימון העברי מופיע אף תשע פעמים בנוסח המסורה של התנ"ך, והוא ידוע בשם "נו"ן הפוכה". בגמרא נאמר כי משמעות סימון זה היא "לומר שאין כאן מקומו"[2], או למעט את הדבר "כאכין ורקין שבתורה"[3].
הסוגריים במתמטיקה
במתמטיקה, סוגריים באים לציין שקבוצה מסוימת של פעולות תתבצע לפני השאר, בניגוד לכללי קדימות אופרטורים. לדוגמה: בתרגיל – בעוד 1+2x5 שווה ל־11, (1+2)×5 שווה ל־15.
כאשר יש סוגריים בתוך סוגריים, יש המשתמשים בסוגים שונים של סוגריים, לשם נוחות הקריאה: נהוג כי הסוגריים החיצוניים יהיו המסולסלים, אחר כך יבואו המרובעים ולבסוף העגולים. סדר ביצוע הפעולות הוא הפוך. לעיתים משתמשים רק בסוג הרגיל של סוגריים (זה המצב בשפות תכנות) ולעיתים מציירים את הסוגרים בגדלים שונים, לפי סדר ביצוע הפעולות – מקטן לגדול.
לעיתים משמשים הסוגריים לפעולות מסוימות. למשל, בסוגריים משולשים משתמשים כדי לציין את הממוצע, המכפלה הפנימית, התוחלת או ערך התצפית, בסוגריים מרובעים נהוג היה לציין את הערך השלם של המספר וכיוצא באלו. סוגריים מסולסלים משמשים לציון איבריה של קבוצה.
סוגריים עגולים או מרובעים משמשים לכתיבת מטריצות.
סימון דיראק ("Bra-Ket"), המשמש לתיאור מצבים קוונטיים במכניקת הקוונטים, ואף יכול לשמש לציון וקטורים במרחב וקטורי מופשט ואף פונקציונלים, עושה שימוש בסוגריים מְזֻוִּים – < >.
הסוגריים במחשבים
בנוסף לשימושם המתמטי, בשפות תכנות שונות פרמטרים המועברים לפונקציה נכתבים בסוגריים רגילים – הן בהגדרתה והן בעת שימוש בה. כן משתמשים בסוגריים מרובעים כדי לגשת לאיברים שונים של מערך, בסוגריים מסולסלים לציין בלוקי פקודות, בסוגריים משולשים כדי לציין תגית (למשל ב-HTML) ועוד.
בשפת LISP יש שימוש נרחב במיוחד בסוגריים רגילים וכל הפקודות נכתבות בתוך סוגריים.
הסוגריים כשינויי נוסח
בספרות חז"ל ובספרות ההלכה והאגדה המשתלשלות ממנה, מקובל לציין בסוגריים שינויי נוסחאות באופן הבא: בסוגריים עגולים מציינים נוסחאות שכנראה הן משובשות, אלא שלא רוצים להשמיטן לגמרי על מנת לא לסטות מהצורה שנלמדה במשך הדורות. בסוגריים מרובעים מציינים נוסחאות נכונות שהושמטו בטעות ויש לקרוא אותן.
קישורים חיצוניים
שגיאות פרמטריות בתבנית:ויקישיתוף בשורה
פרמטרי חובה [ שם ] חסרים
- סוגריים, באתר האקדמיה ללשון העברית
הערות שוליים
- ^ 1.0 1.1 1.2 תחומים כללי הפיסוק, באתר האקדמיה ללשון העברית כללי הניקוד - סוג הסוגריים, האקדמיה ללשון העברית
- ↑ תלמוד בבלי, מסכת שבת, דף קט"ו עמוד ב'.
- ↑ תלמוד בבלי, מסכת ראש השנה, דף י"ז עמוד ב'.
סוגריים30399257


