סהרון (גאומטריה)

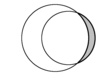
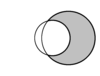
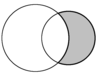
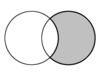
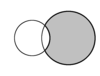
סהרונים (באפור)

בגאומטריה אוקלידית, סהרון הוא שטח החסום בין שתי קשתות מעגליות, אחת מבפנים למעגל והשניה מבחוץ. לעומת זאת, השטח החסום בין שתי קשתות מעגליות בתוך שני המעגלים קרוי עדשה. בשני המקרים, לשתי הקשתות מיתר משותף יחיד.

פורמלית, סהרון הוא משלים לעיגול כאשר שטחו איננו מוכל כולו בעיגול. כלומר, אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B} עיגולים אזי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\cap B} הוא עדשה ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A-(A\cap B)} הוא סהרון.

שטח הסהרון

שטח הסהרון הנוצר על ידי עיגולים שרדיוסיהם הם a ו-b (כאשר b>a) והמרחק בין מרכזיהם הוא c הוא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=2\Delta+a^2\sec^{-1}\left(\frac{2ac}{b^2-a^2-c^2}\right)-b^2\sec^{-1}\left(\frac{2bc}{b^2+c^2-a^2}\right),}

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{sec}^{-1}} הוא הפונקציה ההפוכה של הפונקציה הטריגונומטרית סקאנס וכאשר

$\Delta ={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}$

הוא שטח המשולש שצלעותיו הן a, b ו-c.

תרבוע הסהרון

הסהרון של היפוקרטס

במאה ה-5 לפנה"ס, בנסיונותיו לפתור את אחת הבעיות הגאומטריות של ימי קדם – תרבוע העיגול, הראה המתמטיקאי והאסטרונום היווני היפוקרטס מכיוס כי הסהרון של היפוקרטס ועוד שני סהרונים מיוחדים ניתנים לתרבוע בסרגל ומחוגה.

ב-1766 המתמטיקאי הפיני Daniel Wijnquist, בהתבססו על דניאל ברנולי, הציג חמישה הסהרונים הניתנים לתרבוע, בהשלימו את הרשימה של היפוקרטס מכיוס. ב-1771 לאונרד אוילר הציג גישה כללית לבעיה. ב-1933 וב-1947 הוכיחו ניקולאי צ'בוטריוב ותלמידו אנטולי דורונדוב, באמצעות תורת גלואה, שחמישה סהרונים אלה הם היחידים הניתנים לתרבוע.

ראו גם

• וסיקה פיסקיס
• סאלינון

קישורים חיצוניים

• סהרון, באתר MathWorld (באנגלית)

• The Five Squarable Lunes, MathPages
• M. M. Postnikov, The Problem of Squarable Lunes, The American Mathematical Monthly, August-September 2000, Vol. 107, No. 7, pp. 645-651, in JSTOR

הערות שוליים

הערך באדיבות ויקיפדיה האנגלית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

35789569סהרון (גאומטריה)