מאפיין אוילר
מראה
בטופולוגיה אלגברית ובתורת הגרפים, מאפיין אוילר של גרף מוגדר כ- כאשר E מייצג את כמות הצלעות, F מייצג את כמות הפאות ו-V מייצג את כמות הקודקודים או צמתים. ידוע על פי נוסחת אוילר שלכל גרף מישורי קשיר מאפיין אוילר שווה ל-2; כמו כן, לכל הפאונים האפלטוניים מאפיין אוילר שווה ל-2. כל פאון במישור פרויקטיבי הוא בעל מאפיין אוילר של 1.
באופן כללי יותר, מאפיין אוילר של יריעה עם הומולוגיה נוצרת סופית שווה לסכום המתחלף .
מאפיינים
- אם M × N הוא מרחב מכפלה אז
- אם M ו-N הם מרחב אז המאפיין של ה איחוד שלהם הוא
- למרחב כיסוי מדרגה k אז
דוגמאות
| שם | תמונה | מאפיין אוילר |
|---|---|---|
| קטע | 
|
1 |
| מעגל | 
|
0 |
| כדור | 
|
2 |
| טורוס | 
|
0 |
| טבעת מביוס | 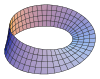
|
0 |
| בקבוק קליין | 
|
0 |
| שם | תמונה | V | E | F | מאפיין אוילר |
|---|---|---|---|---|---|
| ארבעון | 
|
4 | 6 | 4 | 2 |
| קובייה | 
|
8 | 12 | 6 | 2 |
| תמניון | 
|
6 | 12 | 8 | 2 |
| תריסרון | 20 | 30 | 12 | 2 | |
| עשרימון | 
|
12 | 30 | 20 | 2 |
קישורים חיצוניים
- מאפיין אוילר, באתר MathWorld (באנגלית)
- מאפיין אוילר, באתר אנציקלופדיה בריטניקה (באנגלית)
מאפיין אוילר38349418Q852973


