כוח עילוי
עילוי הוא סך כל הכוחות האווירודינמיים או ההידרודינמיים הפועלים על גוף הנמצא בתנועה ביחס לזורם (גז או נוזל) בו הוא שרוי, ומאונכים לכיוון תנועתו. העילוי מאפשר בין היתר לגופים כבדים מן האוויר לעוף.
ישנם מספר הסברים לקיומו של כוח העילוי, והסברים אלה בדרך כלל מציגים פנים שונות של אותם עקרונות פיזיקליים בסיסיים. כוח העילוי נובע, בין היתר, מהפרש הלחצים המופעלים על הגוף הנתון על־פי עקרון ברנולי, כמוסבר להלן. לפי עיקרון זה, ערכו של סכום הלחצים הדינמיים והסטטיים באזור מסוים קבוע. הלחץ הסטאטי מופנה לכל הכיוונים במרחב, ובכלל זה כלפי מעלה. לעומתו, הלחץ הדינמי אינו איזוטרופי וכיוונו תלוי בכיוון התנועה ביחס לזורם. כתוצאה מהפרשי המהירויות של הזורם (או של כל חומר אחר בו נע הגוף) מעל המשטח האווירודינמי, ובהשוואה למהירות התנועה שמתחת למשטח האווירודינמי, עולה הלחץ הדינמי על חשבון ירידה בלחץ הסטטי בחלק העליון של פרופיל הגוף הנע, וכל זאת בהשוואה ללחץ בחלקו התחתון. התוצאה של תהליך זה מביאה להפרש משמעותי בין הלחץ הסטטי מעל הפרופיל לבין הלחץ הסטטי מתחת לפרופיל הגוף הנע, והפרש זה הוא הגורם העיקרי ליצירת כוח העילוי. הסיבה להפעלת כוח העילוי כלפי מעלה מוסברת בכיוון פעולתו של הלחץ הסטטי, וכיוון שלחץ זה פועל לכל הכיוונים וגם כלפי מעלה, וכפי שהוסבר הלחץ הסטטי שמתחת לגוף גדול מזה שמעליו, נוצר כוח העילוי המעלה את הגוף.
הדוגמה לכוח העילוי היא עפיפון הקשור לחוט, שבאמצעותו, ובאמצעות הרוח הפועלת על העפיפון – עולה לאוויר. במקרה זה סכום הכוחות הפועלים על העפיפון מסתכמים מחלוקה אופקית ואנכית של כוחות הרוח הפועלים לדחיפת העפיפון כלפי מעלה, ולעומתם – כוחות החוט, שאף הם מחולקים לחלק האופקי ולחלק האנכי הפועל על העפיפון. בסיכומם של הכוחות הפועלים על העפיפון מאזנים הכוחות האופקיים אלה את אלה, ואילו סיכום הכוחות האנכיים מביא לעילוי העפיפון.
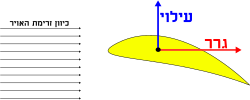
תנועה בתוך זרימה
באוויר (ולמעשה בכל זורם), כוח נוצר כאשר קו זרימה עובר בסביבה של פרופיל אווירודינמי ומוסט כלפי מטה. הכוח שגרם להסטת קו הזרימה כלפי מטה נובע מהמפגש עם הפרופיל האווירודינמי, וכוח שווה ומנוגד לו (על פי חוקי ניוטון) מופעל על הפרופיל האווירודינמי כלפי מעלה. זו הפיזיקה שמאחורי מעוף צלחת מעופפת.
הסטת האוויר כלפי מטה יוצרת עילוי על הגוף שהסיט את האוויר היא תופעה מוכרת הנקראת הסטה מטה (Downwash).
הסטת קו הזרימה כלפי מטה אינה נובעת כתוצאה מ"התנגשות" של מולקולות האוויר בפרופיל והסטתן כלפי מטה מהחלק התחתון שלו, ההסבר הנכון הוא שקווי הזרימה עוקבים אחרי שני צדדי הפרופיל האווירודינמי, וכתוצאה מצורת הפרופיל הזרימה מוטה כלפי מטה. למעשה, האצת הזרימה על ידי הפרופיל מתוארת גם כ"סיבוב" שהפרופיל מפעיל על הזרימה, וניתן לראות זאת גם במערבולות שנוצרות במורד הזרימה.
למעשה, כמעט כל גוף, שיוצב בזווית ביחס לזרימה, יגרום ליצירת עילוי. אולם, רוב הצורות ייצרו באותו אופן גם מידה לא קטנה של גרר, ולפיכך הגוף יהיה לא יעיל אווירודינמית במובן של יחס עילוי לגרר. האתגר העיקרי של מתכנני פרופיל אווירודינמי הוא ביצירת פרופיל שיוצר יחס גבוה בין עילוי לגרר.
ניתן למדוד את עוצמת העילוי על בסיס מודל זה. הכוח הפועל על הכנף הוא בדיוק הפוך לנגזרת בזמן של תנע האוויר. במנהרת רוח, גודל המהירות וכיוונה של זרימת האוויר ניתנים למדידה (למשל במד פיטו, או במד מהירות מבוסס לייזר־דופלר), ומכאן שניתן למצוא את השינוי בתנע ומכאן גם את עוצמת כוח העילוי.
עקרון ברנולי
בקצרה, עיקרון ברנולי אומר שסכום הלחץ הסטטי והלחץ הדינמי הוא קבוע. כלומר, כאשר הלחץ הסטטי יורד הלחץ הדינמי עולה – ולהפך; אך סכומם משתמר.
על פי עקרון ברנולי בזרימה, הגדלה של מהירות הזרימה תגרום לירידה בלחץ. בזרימה ללא חיכוך, קיים קשר הדוק בין עקרון ברנולי לבין חוקי ניוטון ולעקרון שימור האנרגיה הנובע מהם. ההסבר על פי עקרון ברנולי נכון, אולם פעמים רבות מוסיפים להסבר זה הנחות לא נכונות, שמסלפות את המודל הנכון:
- ההנחה שבה החלקיקים שעוברים מעל הפרופיל האווירודינמי ואלה שעוברים מתחתיו חייבים להיפגש לאחר המעבר סביב הפרופיל האווירודינמי אינה נכונה (הנחה זאת נקראת "עקרון זמן המעבר השווה").[1]
- ההנחה כי האצת הזרימה נובעת מההפרש באורך החלק העליון של הפרופיל האווירודינמי ביחס לחלקו התחתון אינה נכונה (הנחה זו היא המשך ישיר להנחה הראשונה).
לאחר שהובהר כי הנחות אלה שגויות, עדיין ניתן להסביר את העילוי ככוח הנובע מהפרש הלחצים מעל ומתחת לפרופיל האווירודינמי. אם נמדוד את מהירות הזרימה בנקודות שונות על פני הפרופיל (הן מעליו והן מתחתיו) ונשתמש במשוואת ברנולי לחישוב הלחץ נגלה שאכן קיים הפרש מהירויות הגורר הפרש לחצים ובעקבות זאת פועל כוח עילוי על הפרופיל האווירודינמי. עם זאת, עקרון ברנולי משמש אך ורק למדידת כוח העילוי באופן שהוסבר, אבל אינו מסביר מדוע הזרימה מאיצה באופן שונה סביב הפרופיל האווירודינמי. אם מניחים כי הזרימה היא זרימה פוטנציאלית, חישוב שקול הכוחות האווירודינמיים (עילוי וגרר) על הכנף נתון על ידי המשוואה הבאה:
כאשר:
- – כוח העילוי ()
- – כוח הגרר ()
- – הגבול של הגוף הבא במגע עם הזרימה
- – הלחץ ()
- – הניצב לפרופיל האווירודינמי
במילים אחרות, נוסחה זו אינה מביאה בחשבון אפקטים של ערבוליות הזרימה (vorticity), חיכוך ודחיסות. בעיקר לא נכון להזניח את הערבוליות שהיא הגורם המרכזי המסביר את העילוי של כנף בזוויות התקפה גבוהות, של כנפי דלתא ושל כנפיים משוכות לאחור.
סירקולציה
אופן שלישי להסביר ולחשב את העילוי הוא על ידי מבנה מתמטי הנקרא סירקולציה. הסבר זה שימושי יותר לאנשים העוסקים בחישובים אווירודינמיים ופחות כהסבר פשוט לאנשים חסרי רקע מתמטי או אווירודינמי. סירקולציה מוגדרת כאינטגרל קווי של מהירות האוויר, במסלול סגור סביב גבולותיו של הפרופיל האוורודינמי. ניתן להבין זאת כשקול ה"סיבוביות" (או ערבוליות) של האוויר סביב הפרופיל. אם הסירקולציה ידועה, אזי העילוי יכול להיות מחושב באמצעות הנוסחה הבאה:
כאשר:
- – צפיפות האוויר, הקטנה ככל שעולים בגובה ()
- – המהירות היחסית בין הכנף לבין האוויר ()
- – הסירקולציה
משפט הלמהולץ קובע כי הסירקולציה היא גודל קבוע, בשל חוק שימור התנע הזוויתי. לפיכך, מטוס במנוחה אינו מפעיל סירקולציה וכאשר מהירות הזרימה גדלה ביחס למטוס, נוצרת מערבולת (Vortex), שנקראת מערבולת התחלתית, בחלקו האחורי של הפרופיל האווירודינמי, בשל אפקטים של חיכוך הזרימה בשכבת הגבול עם הפרופיל. לבסוף, המערבולת ההתחלתית מתנתקת מהפרופיל האווירודינמי ונסחפת במורד הזרימה. בשל משפט הלמהולץ, הסירקולציה סביב הפרופיל האווירודינמי חייבת להיות שווה והפוכה למערבולת ההתחלתית (כדי לשמור על שקול ששווה לאפס, כפי שהיה כשהמטוס היה במנוחה). תאורטית, המערבולת הזו כלואה במשטח הפרופיל האווירודינמי ויוצרת מסלול סגור, אלא שלמעשה מערבולת זו נסחפת גם היא עם הזרימה אל מאחורי המטוס, אולם די בכך כדי ליצור עילוי על הכנף.
נוסחת העילוי ומקדם העילוי
כח העילוי מחושב על פי הנוסחה הבאה –
כאשר –
- – כוח העילוי ()
- – צפיפות האוויר, הקטנה ככל שעולים בגובה ()
- – המהירות היחסית בין הכנף לבין האוויר ()
- – שטח הכנף ()
- – מקדם העילוי (חסר ממדים)
על פי הנוסחה, כוח העילוי תלוי בשני גורמים עיקריים: ריבוע המהירות ושטח הכנף.

מקדם עילוי הוא מספר חסר ממדים המבטא את היחס שבין הכוח הפועל על הכנף בכיוון האנכי לבין שטח הכנף, חצי ריבוע מהירות הטיסה וצפיפות האוויר. מקדם העילוי מושפע בעיקר מהפרופיל האווירודינמי ומזווית ההתקפה של הכנף והוא מחושב באמצעות ניסוי, זווית התקפה גבוהה מדי עלולה לגרום להזדקרות.
שימוש במקדם העילוי מסייע בהבנת ההשפעה של צפיפות האוויר, מהירות הטיסה, ושטח הכנף על העילוי. וכן מאפשר לבצע חישוב מדויק של העילוי שתיצור כנף מסוימת במצב נתון, אך הוא אינו מסייע בהבנה אינטואיטיבית של העילוי ולא מספק כלים לחישוב מקדם העילוי של פרופיל כנף אלא באמצעות ניסוי.
אפקט קואנדה
ג'ף רסקין וחוקרים נוספים טוענים שנדרש להשתמש באפקט קואנדה כדי להסביר את היווצרות עילוי על פרופיל אווירודינמי. הם טוענים שהיצמדות הזרימה אל "עקמומיות הפרופיל" האווירודינמי בחלק שמעל לפרופיל נובעת ברמה המיקרוסקופית מאפקט קואנדה, ושבלעדיו היה נוצר מצב קבוע של הזדקרות. לעומתם, רוב החוקרים מסתפקים בהסברים שניתנו עד כה כדי לחשב ולמצוא את העילוי הנוצר, כשלדעתם אפקט קואנדה אינו נחוץ. עם זאת, תומכי השימוש באפקט מצדיקים את השימוש בו כדי לנתח את העילוי המתפתח על גופים אווירודינמיים ייחודיים, כגון מדפים ואמצעי הגברת עילוי נוספים.
בספרים רבים ובכנסים מדעיים שנוגעים בנושאי תעופה וטיסה נפוץ עדיין ההסבר השגוי הנקרא "עקרון זמן המעבר השווה", הקובע שחלקיקי זרימה, שהפרופיל האווירודינמי מפריד ביניהם, ייפגשו שנית בסיום הפרופיל האווירודינמי באותו זמן. כלומר, החלקיק שמעל הפרופיל יעבור דרך ארוכה יותר בשל עקמומיות משטח הפרופיל מהחלקיק שיעבור מתחת לפרופיל, ובשל הזמן השווה מהירותו הממוצעת של החלקיק העליון תהיה גבוהה יותר, הלחץ שיופעל מעל הפרופיל נמוך יותר (עקרון ברנולי) ומכאן הפרש הלחצים המסביר את העילוי. על אף שהסבר זה הוא הנפוץ ביותר, הוא לא ההסבר היחיד לעילוי הכנף, תופעה נוספת היא החוק השלישי של ניוטון, חוק הפעולה והתגובה, הכנף פוגשת את זרם האוויר בזווית מסוימת (זווית התקפה), זרם האוויר הפוגע בחלק התחתון של הכנף מוסט מטה וכתוצאה מכך הכנף מוסטת מעלה, תופעה זו תורמת לעילוי ומסבירה בין היתר את התופעה של עילוי כאשור המטוס טס הפוך, למטוסים ארובטיים יש פרופיל סימטרי והעילוי הנוצר גם מהפרש הלחצים הנובע מכך שהכנף פוגשת את זרם האוויר בזווית מסוימת הלא היא זווית ההתקפה, הפרופיל סימטרי כדי לאפשר למטוסים אלו טיסה הפוכה בזויות התקפה קטנה יותר, כמו כן למטוסים הטסים במהירויות גבוהות מאוד יש פרופיל כנף בעל עקימון קטן- הכנף דקה יותר, ניתן להבחין בכך כאשר מטוסים אלו טסים במהירות נמוכה והעילוי הנוצר כתוצאה מהעקימון אינו מספק ועל כן הפיצוי באבדן העילוי הנובע מעיקרון ברנולי נעשה על ידי הגדלת העילוי הנובע מחוק הפעולה והתגובה של ניוטון על ידי טיסה בזווית התקפה גבוהה, לצופה מהצד נראה שהמטוס טס עם ״אף״ גבוה יחסית ביחס לאופק.
לקריאה נוספת
- "Introduction to Flight", John D. Anderson, Jr., McGraw-Hill, מסת"ב 0072990716. The author is the Curator of Aerodynamics at the National Air & Space Museum Smithsonian Institute and Professor Emeritus at the University of Maryland.
- "Understanding Flight", by David Anderson and Scott Eberhardt, McGraw-Hill, מסת"ב 0071363777. The authors are a physicist and an aeronautical engineer. They explain flight in non-technical terms and specifically address the Bernoulli myth.
קישורים חיצוניים
- ביקורת של תיאור אופן הטיסה של מטוסים
- הסבר של NASA, הכולל אנימציה להסבר עילוי
- הסבר של עילוי עם אנימציה של הזרימה סביב פרופיל אווירודינמי
- הסבר מעולה מדוע ואיך כנפיים יוצרות עילוי
- מאמר על נוסחת העילוי
- אד רג'יס, תעלומת העילוי האווירודינמי, סיינטיפיק אמריקן, מכון דוידסון לחינוך מדעי, 28 במרץ 2020.
- כוח עילוי, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים
- ↑
 MIT Private Pilot Ground School, Lecture 2 (Aerodynamics), סרטון באתר יוטיוב (אורך: 1:11:45)
MIT Private Pilot Ground School, Lecture 2 (Aerodynamics), סרטון באתר יוטיוב (אורך: 1:11:45)
| כוחות אווירודינמיים | |
|---|---|
|
כוח עילוי38507048Q194433





