סייטסוואפ
סייטסוואפ (באנגלית: Siteswap) היא שיטה להבנה ולתיאור תבניות ג'אגלינג המתארת את קצב הזריקה והמסלול של חפצים באוויר. בדומה לתווים בעולם המוזיקה, השיטה ביססה את מעמדה כשפה באמצעותה ניתן לתקשר ולהבין רצף של זריקות המתאפשרות לביצוע על ידי להטוטן אחד או רבים. כך על ידי מיספור של זריקות לפי גובהן היחסי ולפי מערכת חוקים מתמטית, ניתן לכתוב סדרת מספרים שמתארת תבניות ג'אגלינג.
אפשר ליישם את השיטה לכל מספר של חפצים וידיים. היא אינה מתייחסת לצורת הזריקה (לדוגמה, מאחורי הגב או מתחת לרגל) ואינה מבדילה בין חפצים שונים איתם אפשר ללהטט (לדוגמה כדורים, טבעות, אלות)[1]
מאז המצאת השיטה בשנות ה-80 המוקדמות, הרחיב השימוש בסייטסוואפ את עולם הג'אגלינג לאין שיעור, בהוספה של זן חדש של תבניות למאגר הידע הקולקטיבי ובביסוס הידע אודות התבניות האפשריות לביצוע ואילו שאינן אפשריות. השיטה פותחה במקביל ובאופן עצמאי על ידי 3 קבוצות של מתמטיקאים, שתיים מהן בקליפורניה בשנים 1982 וב-1985, והשלישית בקיימברידג' באותה השנה.
הבסיס: סייטסוואפ א-סינכרוני
סייטסוואפ א-סינכרוני (ידועה גם כ"ונילה סייטסוואפ") היא השיטה הפשוטה והבסיסית ביותר של סייטסוואפ, השיטה מתארת מצב שבו כל יד זורקת בנפרד.
הנחות יסוד
- הזמן שבו מתקיים ג'אגלינג מחולק לחלקים שווים הנקראים "פעימות".
- בכל פעימה זורקת יד אחת (ורק אחת) לסירוגין: בפעימה הראשונה ימין, השנייה שמאל וחוזר חלילה.
- שני כדורים לא יכולים להזרק בו זמנית, גם לא מאותה יד.
- השיטה לא מתחשבת בזמן התפיסה של הכדורים אלא רק בזמן הזריקה הבאה. סייטסוואפ מתייחס לזמן ההחזקה של הכדורים כשווה, וזהו אחד מיסודות השיטה והצורה הטבעית והנפוצה ביותר. אם זמן ההחזקה שווה התפיסה תמיד תהיה מעט לפני הזריקה הבאה, ועל כן הזריקה הבאה והתפיסה משלימות האחת את השנייה.
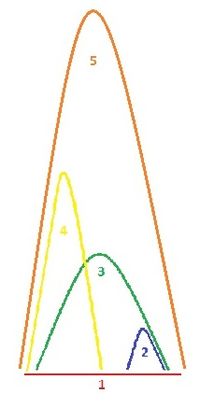
הזריקות השונות ממוספרות, מספר הזריקה מעיד כמה פעימות יעברו עד שהחפץ שנזרק יזרק בשנית. יד ימין זורקת רק בפעימות זוגיות ויד שמאל באי זוגיות או להפך, ולכן, בזריקות של מספרים זוגיים החפץ נוחת בחזרה באותה היד, בעוד שבזריקות של מספרים אי זוגיים החפץ מחליף ידיים. המספר 0 הוא פעימה בזמן שבה ליד הזורקת אין חפץ לזרוק, המספר 1 מתייחס (לרוב) לזריקה שטוחה, העברה מיד ליד - מכיוון שכבר בפעימה הבאה החפץ צריך להזרק בשנית, המספר 2 הוא זריקה ממש נמוכה לאותה היד, לרוב בפועל מיושמת כהחזקה של החפץ למשך הזמן שבו הוא אמור להיות באוויר. המספר 3 הוא זריקה מיד ליד, כמו ב"קסקייד" התבנית הבסיסית של ג'אגלינג ב-3 כדורים, המספר 4 לאותה היד כמו ב"פאונטיין" התבנית הבסיסית של 4 כדורים, המספר 5 כמו בקסקייד 5 כדורים וכן הלאה, כדי למנוע בלבול, מספרים מעל ל-9 נכתבים כאותיות אנגליות החל מ-a=10. בתמונה אפשר לראות הדמיה של גובה יחסי משוערך לזריקות 1,2,3,4,5.
סדרת מספרים אם כן, מתארת סדרת זריקות. רצף זריקות שחוזר על עצמו יוצג כרשימת המספרים הכי קצרה לפני חזרה מטעמי נוחות, כך, המספר 3 מתאר את הזריקות 3333... וכו', נהוג לכתוב את המספר הגבוה בסדרה ראשון, כך, רושמים את הסדרות 315, 153 ו-531 כולן בצורה אחידה כ-531 (ובעצם הן מתארות את אותה התבנית כשמבצעים אותן ברצף).
דיאגרמות סולם

דיאגרמות סולם, הידועות גם כדיאגרמות זמן - מרחב, היו אחת הדרכים הראשונות שמימשו את רעיון הסייטסוואפ והצליחו לתאר תבניות ג'אגלינג. דיאגרמות סולם הן כלי להבנה של סייטסוואפ ומשמשות גם ככלי עבודה ללהטוטנים רבים.
הדיאגרמה מתארת תמונה של תבנית ג'אגלינג, מנקודת מבט עליונה. כל יד שבתמונה מייצגת פעימה בזמן, כשהלהטוטן המדומה שבדיאגרמה צועד קדימה עם כל זריקה. הפעימה הראשונה, פעימה 0, הוא הראשונה מלמעלה ו-11 היא הפעימה האחרונה בתחתית. המספר שמקביל ליד שזורקת מעיד על גובה הזריקה, כל אחד מהקווים, סגול, כחול וירוק עוקב אחר מסלולו של כדור אחד. כך למשל, אנו יכולים לראות שלאחר הזריקה של הכדור הסגול כ-5 בפעימה 0, הכדורים הבאים שנזרקים הם הכדור הכחול, הירוק, הירוק בשנית והכחול בשנית סה"כ 4 פעולות, לפני שבחמישית הכדור הסגול נזרק שוב.
"חוק הממוצע" הנוסחא
חוק הממוצע חל על כל סייטסוואפ תקין, ראשית, כמה הגדרות:
- "אורך המחזור": אורך המחזור הוא כמות הזריקות לפני שהתבנית חוזרת על עצמה. אורך מחזור זוגי נחשב כא-סימטרי מכיוון שאותה היד מתחילה את המחזור החדש, באורך מחזור אי זוגי היד השנייה מתחילה את המחזור החדש ועל כן הוא נקרא - סימטרי.
- "מספר כדורים": כמה כדורים יש בתבנית שלנו.
- "סכום": סך כל המספרים בתבנית מחוברים.
- "סייטסוואפ תקין": רצף מספרים שאפשר לבצע, בתאוריה, ובהמשכיות, ולא נוגד את הנחות היסוד או חוקי השיטה.
- "סייטסוואפ לא תקין": רצף מספרים שאי אפשר לבצע, או נוגד אחת מהנחות היסוד של השיטה.
הנוסחא:
סכום/אורך המחזור=מספר הכדורים
דוגמאות לחוק הממוצע
- סייטסוואפ: 2 סכום: 2 אורך המחזור: 1 כדורים: 2
- סייטסוואפ: 501 סכום: 6 אורך המחזור:3 כדורים: 2
- סייטסוואפ: 531 סכום: 9 אורך המחזור:3 כדורים: 3
- סייטסוואפ: 66771661: סכום 40 אורך המחזור: 8 כדורים: 5
שיטות בדיקה ל"תקינות" של סייטסוואפ
לא כל סדרת מספרים מתארת תבנית לפי סייטסוואפ. כדי לקבוע האם סייטסוואפ הוא תקין, מספר הכדורים לפי חוק הממוצע חייב לצאת שלם. אבל, חוק הממוצע מתקיים גם על חלק מסייטסוואפים לא תקינים, ולכן, לבדו, הוא אינו כלי מספק לבדיקה. אחרי שמוודאים שמספר הכדורים שלם, יש לקבוע האם אף אחד מהכדורים לא מתנגשים זה עם זה.
התנגשויות
כאשר שני כדורים נזרקים לגבהים שבהם הם אמורים להזרק בפעם הבאה באותה הפעימה, נוצרת התנגשות, שהופכת את הסייטסוואפ ללא תקין.
- אם נתעד ברישום את זמני הזריקות (פעימות) והזריקות נוכל לראות בבירור איפה נוצרת התנגשות, ניקח את הסייטסוואפ 531 כדוגמה
| פעימה: | ... | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| זריקה: | ... | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 |
| סכום (פעימה הבאה בה יזרק החפץ): | ... | 9 | 10 | 11 | 6 | 7 | 8 | 3 | 4 | 5 |
מכיוון שכל כדור יזרק בפעם הבאה בפעימה נפרדת אין בסייטסוואפ התנגשויות והסייטסוואפ תקין. לעומת זאת, ניקח לדוגמה את הסייטסוואפ 513
| פעימה: | ... | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| זריקה: | ... | 3 | 1 | 5 | 3 | 1 | 5 | 3 | 1 | 5 |
| סכום (פעימה הבאה בה יזרק החפץ): | ... | 11 | 8 | 11 | 8 | 5 | 8 | 5 | 2 | 5 |
אפשר לראות שהכדורים שנזרקים בפעימות 0,2,4 מתנגשים, כמו גם הכדורים שנזרקים בפעימות 3,5,7 והכדורים שנזרקים בפעימות 6 ו-8, מכאן שהסייטסוואפ אינו תקין - כל שלושת הכדורים שבו מתנגשים.
חישוב מקוצר
בשימוש בחשבון מודולרי ניתן לקצר את הטבלה, ולבדוק התנגשיות לפי מחזור אחד בלבד. כדי לבצע זאת, יש להוסיף עוד שורה בטבלה בה רושמים את הסכום בשארית חילוק של אורך המחזור:
כך למשל ניקח לדוגמה את הסייטסוואפ 813:
| פעימה | 0 | 1 | 2 |
| זריקה | 8 | 1 | 3 |
| סכום | 8 | 2 | 5 |
| סכום בשארית חילוק 3 | 2 | 2 | 2 |
גם המספר 5 וגם המספר 8 משאירים שארית 2 כשמחלקים אותם באורך המחזור 3. מכאן אנו יכולים לדעת שכל הכדורים בתבנית מתנגשים מבלי לרשום מספר מרובה של מחזורים.
עוד שיטה לפישוט תהליך בדיקת ההתנגשויות, היא שימוש בחוק שבעזרתו אפשר לזהות התנגשויות רבות ללא טבלה כלל: כאשר יש שני מספרים בסייטסוואפ, והראשון מביניהם גדול, אם המרחק (בפעימות) בין שני המספרים שווה להפרש ביניהם הסייטסוואפ אינו תקין, לפי חוק זה אפשר לשלול מראש צירופים כ-43, או 3_5.
אפשרויות למודולציה
- אם מוסיפים או מחסרים את המחזור לאחד מהמספרים בסייטסוואפ תקין מקבלים סייטסוואפ תקין חדש עם כדור אחד יותר או פחות בהתאמה.
- אם מוסיפים או מחסרים 1 לכל המספרים בסייטסוואפ תקין מקבלים סייטסוואפ תקין חדש עם כדור אחד יותר או פחות בהתאמה.
- אפשר להחליף "טו סוואפ" (מכאן מקור השם סייטסוואפ) בין שני כדורים בסייטסוואפ תקין – כאשר משאירים את זמן הזריקות והנחיתות של הכדורים זהה אבל משנים את הסדר שבו הם נוחתים. למשל ניקח את התבנית 33, אם זרקנו את הכדור הראשון בפעימה הראשונה ואת הכדור השני בפעימה השנייה הרי שהפעם הבאה שהכדורים האלו יזרקו יהיו בפעימה הרביעית והחמישית בהתאמה, אם נחליף בין הכדורים, הכדור הראשון יזרק שוב בפעימה החמישית והכדור השני יזרק בפעימה הרביעית - מכאן שמספריהם החדשים יהיו 42.
"מצבים" ודיאגרמות מצב (סטייטס)
עד כה, סייטסוואפ בחנה את הזריקות שלנו, ומתי פעם באה יזרק כדור, עוד דרך לגשת לנושא, היא לבחון את ה"מצב" של הכדורים באוויר, זאת אומרת לא להסתכל רק על כדור אחד בכל פעימה אלא לראות את התמונה השלמה של התבנית.
דיאגרמות מצב, מתארות מעין "תחזית" שבה הן מראות כמה זמן יש לכל כדור עד שהוא נזרק שוב, הן מורכבת משורה של משבצות המאוכלסות על ידי הסימנים "X" ו "-", כל משבצת מסמנת פעימה בזמן, אם יש במשבצת כדור היא מסומנת בסימן X ואם אין בסימן - המשבצת השמאלית ביותר היא הזמן הנוכחי, אם יש בה כדור הוא חייב להזרק בפעימה הזו לאחת המשבצות הריקות הפנויות, אם אין בה כדור, הסייטסוואפ של הפעימה הוא 0. כדי לעבור לפעימה הבאה אנו מוחקים את המשבצת השמאלית ביותר ומוסיפים עוד משבצת מצד ימין, אנו משבצים את הכדור שנזרק באחת המשבצות הפנויות.
כך, למשל, המצב XX--X מתאר מצב בו בשתי הפעימות הקרובות נוחת כדור, לאחר מכן יש שתי פעימות פנויות (לעת עתה) ולאחר מכן עוד כדור שנוחת, לאחר שאנו מסירים את הכדור הראשון ומוסיפים עוד משבצת אנו מקבלים את שלב הביניים הזה -X--X(חשוב להדגיש שזה הוא רק שלב ביניים), אנו מתבוננים ורואים איפה אפשר לשבץ את הכדור שזרקנו, הזריקה 1 תפוסה, יש שם X ואם נזרוק 1 תיווצר התנגשות, אם נזרוק 2 נקבל את המצב -XX-X, לחלופין, בזריקה 3 נקבל את המצב -X-XX, המשבצת של 4 תפוסה, ואם נזרוק 5 נקבל את המצב X--XX, אם היינו רוצים לזרוק מספר שהוא יותר גבוה מ-5 כל שהיינו צריכים לעשות הוא להוסיף עוד משבצות, מספר המשבצות קובע את הגובה המקסימלי, בעוד מספר הסימנים X מעיד על כמות הכדורים.
| 7 | 11 | 13 | 14 | 19 | 21 | 22 | 25 | 26 | 28 | |
| (111) 7 | 3 | 4 | 5 | |||||||
| (1011) 11 | 2 | 4 | 5 | |||||||
| (1101) 13 | 1 | 4 | 5 | |||||||
| (1110) 14 | 0 | |||||||||
| (10011) 19 | 2 | 3 | 5 | |||||||
| (10101) 21 | 1 | 3 | 5 | |||||||
| (10110) 22 | 0 | |||||||||
| (11001) 25 | 1 | 2 | 5 | |||||||
| (11010) 26 | 0 | |||||||||
| (11100) 28 | 0 |
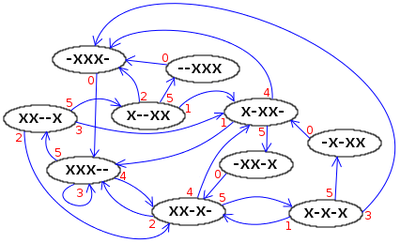
הדיאגרמה שמצד שמאל מתארת את כל המצבים האפשריים ל-3 חפצים ועד לגובה מקסימלי 5, ואת כל המעברים האפשריים ביניהם, אם נעקוב אחרי החצים והמספרים כל סייטסוואפ שיחזיר אותנו למצב בו התחלנו הוא תקין. כל סייטסוואפ ניתן לתיאור בעזרת דיאגרמת מצב אבל אם מעלים את הגובה המקסימלי, הדיאגרמה גדלה לממדי ענק.
מכיוון שדיאגרמות המצב כוללות רק שני סימנים "X" ו"-" הם ניתנות לתיאור על ידי בסיס ספירה בינארי, המצב XX--X ניתן לתיאור גם כ-11001 המטריצה שמימין, היא בעצם אותה הדיאגרמה שמשמאל, ומתארת את כל המצבים וזריקות המעבר ב3 חפצים ועד לגובה מקסימלי 5, כדי להעביר את דיאגרמת המצבים לשיטה בינארית יש להפוך את הצד הימני לזמן הנוכחי, וכך לרשום את המצב XX--X כ- 10011 שערכו הבינארי הוא 19 ולא 25 (11001).
מצב קרקע ומצבים מרוגשים
אם נחזור ונתבונן בדיאגרמה מצד ימין, בפינה השמאלית התחתונה מופע המצב --XXX, שהוא גם המצב היחיד שניתן לחזור אליו על ידי זריקה אחת בלבד, מצב זה נקרא מצב "קרקע", המצב של תבניות הג'אגלינג הבסיסיות, קסקייד ופאונטיין. ללהטוטנים, חשובה ההפרדה בין סייטסוואפים שעוברים דרך מצב קרקע, לכאלה שלא עוברים. סייטסוואפ שלא עובר במצב קרקע נקרא סייטסוואפ במצב "מרוגש".
ההבדל ללהטוטן המבצע הוא מהותי, כדי להגיע לאחד המצבים שבתוך הסייטסוואפ מתוך התבנית הרגילה יש צורך בזריקות "כניסה" וכדי לחזור לתבנית יש צורך בזריקות "יציאה", לדוגמה, כדי להגיע לאחד המצבים שבתבנית 51 שהיא סייטסוואפ מרוגש תקין ב3 כדורים אפשר לזרוק 4 מתוך המצב --XXX כדי לחזור אפשר לזרוק 2, כחוק, הכניסה והיציאה לסייטסוואפ מרוגש תקין תמיד יתחברו לסייטסוואפ תקין נפרד באותו מספר כדורים, (42 - סייטסוואפ תקין ב-3 כדורים)לכן אפשר לחשב את היציאה לפי הכניסה ולהפך.
סינכרוני
סייטסוואפ סינכרוני מתאר תבניות שבהן שתי הידיים זורקות ביחד בכל פעימה, תבניות אלו, יחסית נפוצות בעולם הג'אגלינג, במיוחד במספרים זוגיים של כדורים, אבל גם במספרים אי זוגיים ואפילו בתרגילים פשוטים ב-3 כדורים. מכיוון שבכל פעימה מתבצעות 2 זריקות, הפעימה נרשמת בתוך סוגריים עם פסיק בין שני המספרים, לדוגמה (4,4). מטעמי נוחיות ושמירה על עקביות, מכפילים ב-2 את גובה הזריקה של כל מספר בסייטסוואפ סינכרוני. למשל, תבנית "פאונטיין" סינכרונית ב-4 כדורים (2 כדורים בכל יד) הייתה אמורה תאורטית להרשם כ(2,2) מכיוון שכל כדור נזרק שוב בפעימה שאחרי הבאה, אבל בפועל התבנית נרשמת כ(4,4) וזה משתי סיבות עיקריות:
1. כדי לשמור על התאמה לסייטסוואפ א-סינכרוני, ההכפלה ב-2 גורמת למספרים לתאר את אותן זריקות בשתי השיטות, אחרת הזריקה של 4 כדורים בסייטסוואפ סינכרוני הייתה נכתבת כ-2, אל מול 4 בסייטסוואפ א-סינכרוני.
2. כדי לשמור על חוק הממוצע, בעזרת ההכפלה אפשר עדיין לראות את מספר הכדורים בתבנית לפי החוק.
כתוצאה של ההכפלה סייטסוואפ סינכרוני משתמש רק במספרים זוגיים.
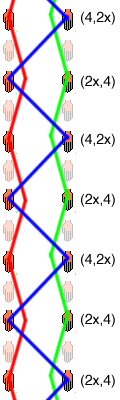
אפשר לדמיין את ההכפלה כהוספה של פעימה ריקה, בין כל פעימה לפעימה כמו בדיאגרמת הסולם שמימין.
לזריקות שמחליפות יד נוסף X אחרי המספר לסימון, למשל התבנית מהדיאגרמה, של התרגיל "בוקס" בשלושה כדורים (4,2X) (2X,4)
הסימן * מעיד שצריך לבצע את התרגיל לסירוגין פעם לצד ימין ופעם לצד שמאל, מכאן, שהתבנית של התרגיל "בוקס" נרשמת כ*(4,2X) והתבנית *(6X,4) (4,2X) היא בעצם (6X,4) (4,2X) (4,6X) (2X,4)
דרך לרשום מצבים בסייטסוואפ סינכרוני היא לרשום אחד על יד השני את המצב של כל יד כאשר כל משבצת מסמנת 2 פעימות כך למשל -XXX XX מתאר מצב שבו בפעימות 2 ו-4 נוחת כדור בכל יד, ובפעימה 6 רק ביד שמאל.
מולטיפלקסים
מולטיפלקס הוא שם לזריקה של יותר מכדור אחד מאותה היד באותה הפעימה. הוא נכתב על ידי סימון בסוגריים מרובעים, הסימון [43] לדוגמה, מסמן פעימה אחת שבה נזרקים מאותה היד 2 כדורים לגבהים שונים 3 ו-4, כל זריקה יכולה להכלל במולטיפלקס חוץ מהזריקה 0 (שיכולה להכלל תיאורתית אבל לא נכללת מסיבות ברורות).
דופלקס הוא השם לזריקה של שני כדורים מאותה יד, טריפלקס של שלושה, קואדרופלקס של ארבעה וכן הלאה, למרות זאת, נהוג בעולם הג'אגלינג להשתמש במונח הכללי מולטיפלקס לתיאור כל המולטיפלקסים השונים. על מנת להבדיל גם בעל-פה בין מולטיפלקסים לזריקות רגילות נהוג לחבר את המספרים למספר דו ספרתי, התבנית 23[43] תקרא כארבעים ושלוש, שתיים, שלוש.
חוק הממוצע ממשיך לחול גם על מולטיפלקסים, כדי שהסייטסוואפ יהיה תקין אנו מחברים את סכום המספרים ומחלקים באורך המחזור, כשהזריקות שבתוך הסוגריים נחשבות כזריקה אחת (מתרחשות באותה הפעימה) 4+3+2+3 = 12/אורך מחזור 3 = 4 כדורים.
"התנגשויות" שהוזכרו בתת-נושא הרלוונטי, במקרה של מולטיפלקסים הן חלק הכרחי מן התבנית, אם משתמשים בשיטת הרישום של כל פעימה וזריקה, יש לוודא שבכל פעימה שבה מתבצעת זריקת מולטיפלקס יש את מספר הכדורים הרלוונטי, ושבפעימות עם זריקות רגילות אין התנגשויות. כדי למנוע התנגשויות פיזיות באוויר או את הצורך לתפוס שני כדורים בבת אחת. נהוג להשתמש ב"זמני החזקה" שונים או בזריקה 2 כהחזקה בפעימה שלפני המולטיפלקס.
עוד דרך לוודא תקינות של סייטסוואפ עם מולטיפלקס היא להתייחס אליו כשני סייטסוואפים נפרדים שחוברו ביחד, כל 2 סייטסוואפים תקינים יכולים ליצור מולטיפלקס תקין ומולטיפלקס לעולם לא יהיה תקין אלא עם הוא יורכב מסייטסוואפים תקינים, למשל הסייטסוואפ 423 (3 כדורים) בחיבור לסייטסוואפ 300 (כדור 1) יוצר את הסייטסוואפ 23[43] אבל גם יכול ליצור את הסייטסוואפים 3[23]4 או [33]42 כולם תקינים ב־4 כדורים, אי אפשר לחבר סייטסוואפים בעלי אורך מחזור שונה, ועל כן כדי לחבר כאלה יש לשנות את אורכם על ידי חישוב הכפולה המשותפת שלהם.
בהסבה של מצבים לזריקות מולטיפלקס, אי אפשר להשתמש בשיטה הבינארית, מכיוון שיש יותר משני משתנים.
סייטסוואפ ביותר משתי ידיים
סייטסוואפ לא מתייחסת לכמה ידיים משתתפות בתבנית, השיטה קובעת רק את סדר הכדורים, כל סייטסוואפ תקין ניתן לביצוע בכל מספר ידיים (לא כולל 0). השימוש בסייטסוואפ בפאסינג (מסירות בין שני להטוטנים או יותר) הוא יחסית פחות נפוץ, זאת משום שפאסינג הוא תחום קשה יותר של ג'אגלינג, והשיטה המתמטית יותר קשה להבנה. ועם זאת, רבות מהתבניות הפופולריות בתחום הפאסינג נוצרו דרך שימוש בסייטסוואפ שהוא חלק בלתי נפרד מהתפתחות התחום.
א-סינכרוני
בסייטסוואפ א-סינכרוני בסיסי בכל פעימה נזרק כדור אחד. שיטה זה עובדת גם ליד אחת, 3 או 4 ידיים ואפילו יותר. כך נראית טבלה המתארת את הסייטסוואפ 756 (תקין ל-6 כדורים), המבוצע על ידי שני להטוטנים (4 ידיים):
| פעימה: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| להטוטן א' | 7 | 6 | 5 | 7 | 6 | ||||
| להטוטן ב' | 5 | 7 | 6 | 5 |
אפשר לראות בטבלה שכל אחד מהלהטוטנים זורק רק בחצי מהפעימות, מכאן נוצרת חלוקה ל־2 סוגים של סייטסוואפים, שמתקיימים יחד, כאשר מעורב יותר מלהטוטן אחד: מקומי, וגלובלי.
- הסייטסוואפ הגלובלי הוא הסייטסוואפ התקין, שמתאר את התבנית השלמה של כל הכדורים באוויר, תיאור גרפי של סדר הזריקות בטבלה כמו הטבלה שלמעלה יהיה בצורת זיג זג בין שני הלהטוטנים. במקרה של הטבלה המתוארת, הסייטסוואפ הגלובאלי הוא 756.
- הסייטסוואפ המקומי הוא רצף הזריקות שכל להטוטן מבצע באופן עצמאי ובלי תלות בחוקי התקינות של סייטסוואפ. תיאור גרפי של סדר הזריקות יהיה בצורת שני קווים ישרים אופקיים. במקרה של הטבלה המתוארת הסייטסוואפ המקומי של שני הלהטוטנים הוא 765 - סייטסוואפ לא תיקני בתור סייטסוואפ סולני.
- אם אורך המחזור של הסייטסוואפ הגלובאלי הוא שונה ממספר הלהטוטנים או מכפולה של מספר הלהטוטנים, הסייטסוואפ המקומי תמיד יהיה אותו סייטסוואפ לכל הלהטוטנים אך בהטיית זמן, למשל 765 מול 576.
- לעיתים, בסייטסוואפ ביותר משתי ידיים, נהוג לחלק את מספרי הזריקות במספר שיביא את כמות הידיים ל-2, זאת כדי שהזריקות יתאימו לגבהים של זריקות רגילות בסייטסוואפ ב-2 ידיים. כך למשל, בסייטסוואפ ב-4 ידיים נהוג לעיתים לחלק את כל מספרי הזריקות ב-2. שיטה זו, אינה מאוד נפוצה כי היא יוצרת מספרים לא שלמים במסירות (במיוחד עם מחילים אותה על יותר מ4 ידיים ואז נוצרים שברים קטנים מחצי). כשמחלקים את המספרים נהוג להוסיף למסירות את האות P לציין שזו מסירה.
סייטסוואפ לא קובעת איך להעמיד את הלהטוטנים במרחב, ניתן להעמידם בכל צורה אפשרית, והיא גם אינה מתייחסת לסדר הידיים הזורקות, אבל, ישנה צורה מקובלת לסדר הזריקות והיא א' יד ימין, ב' יד ימין, ג' יד ימין א' יד שמאל, ב' יד שמאל ג' יד שמאל (במקרה של שלושה להטוטנים)
מקרה יותר נפוץ הוא שני להטוטנים. במקרה זה, אם שומרים על הסדר המקובל, זריקות של מספרים אי זוגיים נהיות מסירות ללהטוטן השני וזריקות של מספרים זוגיים לא מחליפות צד.
חצי מהמספרים האי זוגיים, ימסרו ליד ימין של הלהטוטן השני וחצי ליד שמאל, לכן 1,5,9 וכו' ימסרו מלהטוטן א' באלכסון ומלהטוטן ב' בקו ישר, בעוד ש3,7 וכו' ימסרו מלהטוטן א' בקו ישר ומלהטוטן ב' באלכסון.
כנ"ל לגבי המספרים הזוגיים, אלו שהם כפליים מספר זוגי יישארו באותה יד ואלו שהם כפליים מספר אי זוגי יזרקו ליד השנייה. 2,6 וכו' יישארו אצל אותו להטוטן אך יחליפו יד, בעוד ש 4,8 וכו' נשארים אצל אותו הלהטוטן באותה היד.
סייטסוואפ א-סינכרוני ליד אחת נפוץ בעיקר בתחום הדיאבולו, מכיוון שיש רק יד אחת, המספרים השונים מקבילים לכפליים ערכם בסייטסוואפ רגיל ב-2 ידיים, 1 הוא "החזקה" או זריקה מאוד נמוכה, 2 הוא מקביל ל-4 בסייטסוואפ רגיל וכו'.
סינכרוני
על אף שהרבה תבניות פאסינג מתבססות על קצב א-סינכרוני, עדיין יש רוב משמעותי לתבניות סינכרוניות, כל סייטסוואפ סינכרוני (בעל שתי זריקות בכל פעימה) ניתן לטרנספורמציה פשוטה לסייטסוואפ ב-4 ידיים, שיטת הטרנספורמציה עובדת לפי הסדר: (א' ימין, ב' ימין) (א' שמאל, ב' שמאל):
- כל אחד מהלהטוטנים מקבל צד בסוגריים, כך, סייטסוואפ סינכרוני נרשם כ- (ימין, שמאל), להטוטן א' תמיד יקבל את צד ימין ולהטוטן ב' תמיד יקבל את צד שמאל.
- X ב-4 ידיים הופך ל-P, מסירה, באופן טבעי מכיוון שהוא חוצה צד בסוגריים.
- מכיוון שכל המספרים זוגיים בסייטסוואפ סינכרוני, החלוקה ב-2 לא כוללת שברים ולכן נפוצה יותר מבפאסינג סייטסוואפ א-סינכרוני.
- באותה צורה כמו בסייטסוואפ א-סינכרוני, חצי מהמסירות נמסרות בקו ישר וחצי באלכסון, אך הפעם שני הלהטוטנים מוסרים את אותם המספרים ישר ובאלכסון. כך, 2X ו6X הופכים להיות 1P ו-3P ונמסרים ישר, כאשר 4X ו8X הופכים להיות 2P ו-4P ונמסרים באלכסון.
- כדי לוודא לאן נזרקים הכדורים שאינם מסירות אנו מחלקים ב-2 ומשתמשים בזריקות המקבילות בסייטסוואפ סולני.
הרחבת השיטה למסירות בקצב סינכרוני ליותר מ-2 להטוטנים משתמשת בשיטה הלא נפוצה להרחבת סייטסוואפ סינכרוני (...y,y,y) שיטה זו עובדת לפי אותו עקרון של סייטסוואפ סינכרוני רגיל, רק שבין כל זריקה נוספת עוד פעימה ריקה על כל כדור שנוסף לביט.
חיבור סייטסוואפים סולנים
דרך יותר מקובלת ליצור תבניות התמסרות סינכרוניות היא להעמיד מספר סייטסוואפים סולנים בטבלה, ולהחליף זריקות בודדות בתבנית למסירות, העקרון פשוט: שני להטוטנים מקבלים בפעימה מסוימת כדור, במקום שלהטוטן א' יזרוק לעצמו ולהטוטן ב' יזרוק לעצמו להטוטן א' מוסר לב' וב' לא'. את אותו עקרון ניתן ליישם גם על מספר רב של להטוטנים.
שיטת פרישאק
שיטת פרישאק (Prechac) היא שיטה ליצור תבניות פאסינג סימטריות, קאנוניות, בשימוש בסייטסוואפ סולני. השיטה מתבססת על החוקים למודולציה של סייטסוואפ, ובאמצעותה ניתן ליצור בפשטות תבניות רבות. השיטה מאוד פופאלרית בקהילות הג'אגלינג הגרמניות והצרפתיות, ומהווה חידוש משמעותי שנוסף לעולם הפאסינג לקראת סוף שנות ה-90.
לפי שיטת פרישאק אפשר להציב כל סייטסוואפ סולני בטבלה שהשורות בה הן כמספר הלהטוטנים והעמודות מייצגות קאנון שווה של המחזור, אם המחזור זוגי מספר העמודות שווה לאורך המחזור ואם הוא אי זוגי מספר העמודות שווה לאורך המחזור כפול מספר הלהטוטנים.
לכל אחת מהזריקות ניתן להוסיף או לחסר 1 חלקי מספר הלהטוטנים המשתתפים מאורך המחזור ולהוסיף את האות P לזריקה. לדוגמה, אם מספר הלהטוטנים הוא 2 ואורך המחזור הוא 4 ניתן להוסיף או לחסר חצי 4 = 2 ולהוסיף את האות P לכל אחד המספרים בסייטסוואפ.
ס"כ הכדורים בתבנית שווה לס"כ הכדורים בסייטסוואפ הסולני כפול מספר המשתתפים +- כדור על כל P שנוסף בהתאמה לצורת הוספת הP על ידי חיבור או חיסור.
זמן החזקה
זמן החזקה (אנגלית dwell time) מתייחס לזמן, שבו הלהטוטן מחזיק את הכדור ביד בין זריקה לזריקה. זמן החזקה ארוך יחסית מביא לתבנית איטית, בעוד שזמן החזקה קצר יחסית מביא לתבנית מהירה. זמן ההחזקה משתנה בין להטוטן ללהטוטן וגם בקשר ישיר לתבניות שונות שאותו להטוטן מבצע. זמן התפיסה הממוצע ברוב התבניות, הוא בין חצי פעימה לפעימה שלמה אחרי שהיד הזורקת שיחררה את הכדור, לפיכך, ומכיוון שבסיטסוואפ בשתי ידיים כל יד זורקת פעם ב-2 פעימות זמן ההחזקה הממוצע הוא בין פעימה לפעימה וחצי. שינוי של זמן ההחזקה לאורך לא אחיד נוגד את הנחות היסוד של סייטסוואפ, אך במציאות, להטוטנים משתמשים לעיתים בזמן החזקה לא אחיד, בתרגילים ספציפיים בהם קשה יותר לשמור על זמן החזקה אחיד, או כדי לאפשר לעצמם יותר חופש וגמישות פעולה - "למתוח" את התבנית שהסייטסוואפ מכתיב. זמן החזקה לא אחיד, שימושי במיוחד בהגדרות מקרים חריגים ותבניות לא שוות מבחינה קצבית, ובתבניות עם זריקות מולטיפלקס, כדי להימנע מהתנגשויות או צורך לתפוס שני כדורים בבת אחת.
שימושים נפוצים
- מעבר לתרומה הכללית לעולם הג'אגלינג על ידי הוספה של אין ספור תבניות חדשות למגוון האפשרויות, סייטסוואפ משמשת ככלי ללהטוטנים רבים בעבודה בשגרת האימונים. מכיוון שהשיטה אינה מתארת סוגים שונים של זריקות היא משאירה חופש רב בצורת הביצוע של רצף המספרים. כך להטוטנים נוהגים לקחת סייטסוואפ ולשנות את צורת הזריקה (מאחורי הגב, מתחת לרגל ועד זריקות גוף רבות ומגוונות) או את צורת התפיסה, או להוסיף מימד של תנועה בחלל, כל זאת תוך כדי שימוש באפשרויות הטמונות בכל אחד מהמספרים.
- סייטסוואפ עוזר ללהטוטנים רבים ללמוד תרגילים קשים, כשבאמצעותו אפשר להשתמש באחת מצורות המודולציה כדי להפיק סייטסוואפ דומה אך במספר קטן של כדורים או אורך מחזור קצר יותר.
- בתחום הפאסינג (התמסרות בין שני להטוטנים או יותר) סייטסוואפ ממשיך לאפשר למחשבה על תבניות חדשות שלא נוסו, מכיוון שמגוון האפשרויות הוא רחב יותר, וקשה יותר ליצור תבניות ללא עזרת השיטה מאשר בלהטוטנות סולנית, התפתחות התחום קשורה הדוקות בשיטה.
סימולטורים
קיימות תוכנות חינמיות רבות שמאפשרות לראות הדמיה של להטוטן מבצע תרגילים, וסייטסוואפים שונים:
- http://quantumjuggling.com/(הקישור אינו פעיל) סימולטור חדש ומשוכלל מבית היוצר של פול קילמק אחד ממציאי השיטה.
- https://web.archive.org/web/20070825123957/http://jugglinglab.sourceforge.net/ אנימטור קוד פתוח בJava
- https://web.archive.org/web/20060925102220/http://www.siteswap.net/applet.html עוד סימולטור מוצלח בjava
- http://www.jug.co.il אתר לימוד תרגילים בכדורים בעברית, המשתמש בסימולטור jugglingLab ומכיר גם אותו.
ראו גם
- להטוטנות (ג'אגלינג)
לקריאה נוספת
- burkard polster The Mathematics of Juggling, Springer-Verlag, New York, 2003
קישורים חיצוניים
- [1] : מתוך האתר המקיף ביותר בתחום הלהטוטנות מקבץ מאמרים על סייטסוואפ ונושאים קשורים (אנגלית)
- http://www.juggling.org/jw/91/2/notation.html : מאמר של ברוס טיימן, אחד מממציאי השיטה, בימיה הראשונים. (אנגלית)
- https://web.archive.org/web/20110317123352/http://www.siteswapgeneration.com/ אתר עדכני המוקדש לנושא כולל פורום. (אנגלית)
- https://web.archive.org/web/20101228032650/http://www.jugglewiki.org/wiki/Main_Page : אתר הויקי המוקדש לג'אגלינג כולל הדמיות של אלפי תרגילים וגם כמה מאמרים על סייטסוואפ. (אנגלית)
- http://www.twjc.co.uk/calculator.html : מחשבון לחישוב האם סייטסוואפ הוא תקין (אנגלית)
- http://prechacthis.org/ : אתר שמייצר תבניות פאסינג סימטריות קנוניות, לפי שיטת פרישאק.
- https://web.archive.org/web/20110317042052/http://www.passingdb.com/articles.php מקבץ מאמרים באנגלית וצרפתית מתוך האתר המקיף בתחום הפאסינג, כולל שורה של מאמרים שכתב כריסטוף פרישאק.
הערות שוליים
- ↑ למרות האמור, בעת תיאור תבניות ג'אגלינג מעשיות ישתמש ערך זה בשם "כדורים" במקום "חפצים" מטעמי נוחיות
סייטסוואפ32513340Q1389933


