תרשים Q-Q


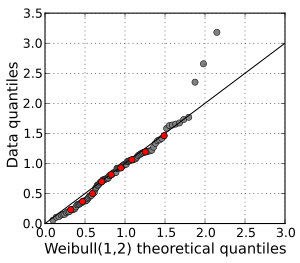

בסטטיסטיקה, תרשים Q-Q (כאשר "Q" הוא קיצור quantile; שברון) הוא תרשים הסתברות ודרך גרפית להשוואה בין שתי התפלגויות באמצעות הצגת השברונים שלהן אלו מול אלו. ראשית נבחרת קבוצת מרווחים לשברון. נקודת (x,y) בתרשים מתאימה לשברון מההתפלגות השנייה (הקואורדינטה y) למול השברון המתאים בהתפלגות הראשונה (הקואורדינטה x).
כאשר שתי ההתפלגויות שאותן משווים הן זהות, הנקודות בתרשים Q-Q ימצאו בקרבת הקו הישר y=x. אם יש קשר ליניארי בין ההתפלגויות, הנקודות בתרשים Q-Q ימצאו בקרבת קו ישר, אך לא בהכרח y=x. תרשים Q-Q יכול לשמש כאמצעי גרפי לשערוך פרמטרים במשפחה של התפלגויות התלויות מיקום וסקלה.
תרשים Q-Q משמש כדי להשוות את הצורה של ההתפלגויות, ומספק המחשה גרפית לתכונות כמו מיקום, סקלה וצידוד של שתי התפלגויות. תרשימי Q-Q יכולים לשמש להשוואה של נתוני תצפיות, או התפלגויות תאורטיות. ניתן לראות את השימוש בתרשימי Q-Q להשוואת שני מדגמי נתונים כדרך א-פרמטרית להשוואה בין ההתפלגויות שלהם. תרשים Q-Q הוא לרוב אמצעי חזק יותר להשוואה בין התפלגויות מאשר היסטוגרמות של שתי התפלגויות. שימוש נפוץ לתרשימי Q-Q הוא להשוואה בין התפלגות נתונים בתצפיות למודל תאורטי להתפלגות, וכך ניתן להמחיש את ההתאמה בין ההתפלגויות באופן חזותי. שימוש נפוץ נוסף הוא להשוואה בין שתי התפלגויות תאורטיות. יתרון של שימוש בתרשימי Q-Q על פני תרשים פיזור (scatter plot) הוא שאין צורך שהתצפיות יבואו בזוגות, ומספר התצפיות מכל אחת מהקבוצות לא חייב להיות שווה.
המונח "תרשים התפלגות" מתייחס לעיתים לתרשים Q-Q, ולעיתים מתייחס למחלקה כללית יותר של תרשימים, ולעיתים לתרשים P-P. המתאם בתרשים התפלגות הוא מדד הנשען על רעיון דומה לזה של תרשימי Q-Q, ומודד את ההתאמה בין התפלגות לתצפיות הנצפות, ומשמש לעיתים כאמצעי להתאמת ההתפלגות לנתונים.
תיאור ובנייה
תרשים Q-Q הוא תרשים של שברונים או ההערכה של שברונים של שתי התפלגויות אלו מול אלו. תבנית הנקודות בתרשים משמשת להשוואה בין ההתפלגויות.
השלב העיקרי בבניית תרשים Q-Q הוא לחשב או לשערך את השברונים בתרשים. אם ציר אחד או שני הצירים בתרשים מתבססים על התפלגות תאורטית עם פונקציית הצטברות (CDF) רציפה, כל השברונים מוגדרים היטב וניתנים לחישוב כהיפוך של פונקציית ההצטברות. אם ההתפלגות התאורטית היא ללא פונקציית הצטברות רציפה, ייתכן שחלק מהשברונים אינם מוגדרים, אך ניתן במקרה כזה להשתמש באינטרפולציה. אם ה-Q-Q מתבסס על נתונים שנצפו נדרש לשערך את השברונים ולכך קיימות שיטות שונות.
מקרה פשוט הוא כאשר שתי קבוצות הנתונים הן בעלות גודל זהה. במקרה זה על מנת ליצור תרשים Q-Q, ניתן למיין כל אחת מהקבוצות בסדר עולה ולצייר כל זוג מהקבוצות הממוינות. כאשר שתי הקבוצות אינן בעלות גודל אחיד יצירת התרשים עשויה להיות מורכבת יותר, ועשויה להצריך אינטרפולציה על השברון המשוערך כך שהשברונים יתאימו יתאימו להסתברות המקור.
בצורה אבסטרקטית יותר בהינתן שתי פונקציות הצטברות F ו G, עם פונקציות הופכיות F−1 ו G−1, תרשים Q–Q מצייר את השברון ה q של F כנגד השברון ה-q של G עבור טווח ערכים של q. תרשים Q–Q הוא אפוא עקום פרמטרי על פני הטווח [0,1] עם ערכים ממשיים במישור R2.
פירוש
כאשר מסתכלים על תרשים Q-Q משמאל לימין, הנקודות בתרשים Q-Q הן תמיד לא יורדות. אם שתי ההתפלגויות שאותן משווים הן זהות, הן יראו בתרשים Q-Q כקו y=x. אם שתי ההתפלגויות מסכימות לאחר פעולה ליניארית לתיקון הערכים של אחת ההתפלגויות, יופיעו הנקודות על קו ישר, אך לא בהכרח y=x. אם העקומה נמצאת מתחת לקו y=x אז ההתפלגות האופקית היא מפוזרת יותר ביחס להתפלגות האנכית (ולהפך כאשר העקומה נמצאת מעל לקו). תרשימי Q-Q הם לעיתים בצורת קשת או צורת "S", מה שמעיד על כך שהאחת ההתפלגויות מצודדת יותר מהשנייה או שאחת מהן היא בעלת זנב ארוך יותר מהשנייה.
אף על פי שתרשים Q-Q מבוסס על שברונים, בתרשים Q-Q סטנדרטי לא ניתן לקבוע איזו נקודה ב-Q-Q מגדירה שברונים מסוים. לדוגמה לא ניתן לקבוע את החציון של אף אחת משתי ההתפלגויות שמשוות בתרשים. לעיתים מציינים את העשירונים בתרשימי Q-Q על מנת לאפשר זאת.
השיפוע וההזזה של רגרסיה ליניארית בין שברונים נותנים מדד למיקום היחסי ולסקלה היחסית של הדוגמאות. אם החציון של ההתפלגות מצויר על הציר האופקי בנקודה 0, ההזזה של רגרסיה ליניארית הוא מדד למיקום והשיפוע הוא מודד לסקלה. המרחק בין החציונים הוא מדד נוסף למרחק יחסי שמשתקף בתרשים Q-Q. "מקדם המתאם של תרשים ההסתברות" הוא מתאם פירסון בין זוגות של שברונים. ככל שהמקדם קרוב יותר ל-1, קרובות יותר ההתפלגויות זו לזו.
שימוש נפוץ נוסף של תרשימי Q-Q הוא להשוואה בין התפלגות במדגם להתפלגות תאורטית, כדוגמת התפלגות נורמלית, N(0,1), בדומה לתרשים התפלגות נורמלית.
מיקומים בתרשים
בחירת השברונים מההתפלגות התאורטית תלויה בהקשר ובמטרה. דרך אחת היא שבהינתן מדגם בגודל n, לבחור את k/n עבור k=1..n שכן אלו הדוגמאות של ההתפלגות. האחרונה שבהן n/n מתאימה לשברון העליון - הערך המרבי של ההתפלגות התאורטית עשוי לעיתים להיות אינסופי. בחירות אחרות הן k-0.5/n או לרווח את הנקודות תחת התפלגות אחידה ולהשתמש בk/(n+1).
קישורים חיצוניים
תרשים Q-Q26598441


