ספקטרוסקופיית מסבאואר

ספקטרוסקופיית מסבאואר היא טכניקת ספקטרוסקופיה המבוססת על אפקט מסבאואר ועל אפקט דופלר. אפקט מסבאואר, שהתגלה על ידי רודולף מסבאואר (גרמנית: "Mößbauer") ב-1958, מסביר כיצד קרני גמא נפלטות ונבלעות במעברים ברמות האנרגיה של הגרעין כמעט ללא רתיעה כאשר האטום הפולט הוא חלק מסריג מוצק. באמצעות אפקט מסבאואר ניתן לבצע ספקטרוסקופיה הרגישה מאוד לסביבה הכימית של הגרעין הנחקר.
בדרך כלל, ניתן להשתמש בשיטה כדי לאפיין שלושה סוגים של אינטראקציות המשפיעות על רמות האנרגיה של הגרעין: הסטה איזומרית - שינוי בהזזת האנרגיה המשותף לכל המצבים הקוונטיים של הגרעין ונובע מהבדלים בצפיפות האלקטרונים הסמוכה (נקראת גם הסטה כימית), פיצול קוודרפול -פיצול של רמות האנרגיה עקב גרדיאנט בשדה החשמלי בסביבות הגרעין, ופיצול זימן מגנטי - פיצול ברמות האנרגיה עקב שדות מגנטיים הנובעים מהאלקטרונים בסביבת הגרעין.
בשל האנרגיה הגבוהה ורוחב הקו הצר של קרני גמא ממעברים גרעיניים, ספקטרוסקופיית מסבאואר היא טכניקה רגישה ביותר מבחינת רזולוציית אנרגיה (ומכאן תדר), המסוגלת לזהות שינויים של עשרות ננו אלקטרון וולט ביחס למעברי אנרגיה של קילו אלקטרו וולט.
עיקרון פעולה בסיסי
קרני גמא גרעיניות ורוחב הקו
כאשר גרעין דועך באופן רדיואקטיבי לגרעין אחר (לדוגמה באמצעות דעיכת בטא), המצב האנרגי הקוונטי של הגרעין החדש שונה מהמצב ברמת היסוד. במצב כזה, הגרעין החדש ידעך לרמת היסוד הגרעינית ויפלוט קרינה אלקטרומגנטית שתסחוב איתה את עודף האנרגיה. הפרשי האנרגיה בין מצבי האנרגיה השונים של הגרעין הם מסדר גודל של עשרות קילו אלקטרון וולט (לדוגמה - בדעיכת של ברזל-57 האנרגיה היא 14.4 קילו אלקטרון וולט) ולכן הפוטונים הנפלטים במהלך הדעיכה הם באנרגיה מסדר גודל כזה, ולכן הם מהווים קרינת גמא.
הזמן האופייני לדעיכה בין רמות האנרגיה הגרעיניות הוא מסדר גודל של מאות ננו-שניות (לדוגמה - בברזל-57 הזמן האופייני הוא 140 ננו-שניות). בהתאם לעקרון אי-הודאות של הייזנברג הזמן האופייני קובע אי-ודאות באנרגיה של הדעיכה מסדר גודל של ננו-אלקטרון וולט בודדים (בברזל-57 - 2.4 ננו אלקטרון וולט). אי הודאות הזו היא אינהרנטית לדעיכה, ואיננה נובעת משגיאה באמצעי המדידה. להרחבה הזו של הקו הספקטרלי קוראים הרחבה טבעית. באופן דומה, כאשר קרינת גמה עוברת בקרבת גרעין היא יכולה לערער את הגרעין לרמה שונה מרמת היסוד אם ההפרש בין האנרגיה של הקרינה לאנרגיה של המעבר הגרעיני הוא מסדר גודל של רוחב הקו.
רתיעה גרעינית
בדיוק כפי שאקדח נרתע כאשר כדור נורה, שימור התנע דורש שגרעין הפולט קרינה אלקטרומגנטית יירתע במהלך הפליטה של קרן הגמא. אם גרעין במנוחה פולט קרן גמא, אנרגיית הגמא קטנה מעט מהאנרגיה של המעבר בין רמות האנרגיה הגרעיניות. על מנת שגרעין במנוחה יספוג קרן גמא, אנרגיית קרן הגמא צריכה להיות מעט גדולה מאנרגיית המעבר הטבעית.
ביחס לאנרגיה של המעבר האנרגיה של הפוטון היא מסדר גודל של (כאשר אנרגיית המעבר, ו- אנרגיית המנוחה של הגרעין, המינוס מתקבל עבור קרינת גמא הנפלטת מדעיכה והפלוס עבור קרינה הפוגעת בגרעין ומערערת אותו). מאחר שאנרגיית המנוחה של הגרעין היא מסדר גודל של מאות ג'יגה אלקטרון וולט נקבל שההפרש בין האנרגיה של קרינת הגמא לאנרגיה של המעבר היא מסדר גודל של מילי אלקטרון וולט. כלומר ההפרש גבוה בהרבה מרוחב הקו של המעבר. המשמעות היא שפליטה ובליעה של אותה קרן גמא על ידי גרעינים זהים באמצעות מעבר בין אותם רמות אנרגיה בגרעינים שונים אינה אפשרית עם גרעינים חופשיים, מכיוון שהרתיעה גורמת לכך שהאנרגיה של הקרינה הנפלטת קטנה מדי. כאשר פליטה ובליעה כזו אפשריות חלק ניכר מהקרינה ייבלע והבליעה תיקרא בליעה בתהודה.
אפקט מסבאואר
גרעינים בגביש מוצק, לעומת זאת, אינם חופשיים להירתע מכיוון שהם קשורים במקומם בסריג. כאשר גרעין במוצק פולט או סופג קרן גמא, אנרגיה מסוימת עדיין יכולה ללכת לאיבוד כאנרגיית רתיעה, אך במקרה זה היא האנרגיה של הרתיעה היא ברמות אנרגיה מקבלות ערכים בדידים, רמות אנרגיה אלה מאפיינות תנודה של הסריג ונקראות פונונים. בבליעה או פליטה כזו, ניתן לפלוט כל מספר שלם של פונונים, כולל אפס, אירוע הידוע כאירוע "ללא רתיעה". במקרה כזה, שימור התנע מסופק על ידי התנע של הגביש בכללותו, כך שלמעשה האנרגיה הקינטית של הסריג היא אפסית, וכל האנרגיה של המעבר הגרעיני עוברת לקרינת הגמא.[1]
מסבאואר מצא שבסריגים מסוימים חלק ניכר מאירועי הפליטה והספיגה יהיו נטולי רתיעה. כמות האירועים הללו ניתנת לכימות באמצעות פקטור לאמב-מסבאואר. האפקט בו גרעין בסריג פולט קרינה ללא רתיעה נקרא אפקט מסבאואר, והוא שמאפשר את ספקטרוסקופיית מסבאואר העושה שימוש בקרינת גמא הנבלעת בתהודה, כאשר גם הפליטה וגם הבליעה מתבצעות ללא רתיעה.
הסחת דופלר
אפקט מסבאואר מאפשר לקרינה הנפלטת מסריג מסוים להיקלט בתהודה בסריג של אותו חומר בדיוק בו אנרגיות המעבר הגרעיניות שוות בדיוק. אולם אין בכך די כדי לאפשר ספקטרוסקופיה של דגימות שונות במקצת. כדי לאפשר ספקטרוסקופיה כזו, נעשה שימוש באפקט דופלר. אם הגרעין שפולט את הקרינה נמצא בתנועה ביחס לגרעין שקולט אותה, מתבצעת הסחת דופלר של הקרינה, והאנרגיה של הגמא כפי שנצפית בגרעין הקולט היא (כאשר היא המהירות היחסית בין הגרעינים ו- מהירות האור). באמצעות הזזה של הגרעין הפולט במהירויות שונות, ניתן למדוד את המהירות בה יש להזיז את הסריג בו נמצא הגרעין הפולט כדי לאפשר לו להיקלט בגרעין בדגימה. מאחר שאנרגיית המעבר היא מסדר גודל של קילו אלקטרון וולט, מספיק להזיז את הסריג הפולט במהירות של מילימטרים בודדים לשנייה כדי לאפשר הזזה של אנרגיית הפוטון בעשרות ננו אלקטרון וולט.
שיטה אופיינית
בצורה הנפוצה ביותר ספקטרוסקופיית מסבאואר מבוצעת באמצעות בליעה. בשיטה זו, דגימה בסריג מוצק נחשפת לקרן של קרינת גמא הנפלטת מסריג אחר, וגלאי מודד את עוצמת הקרן המועברת דרך הדגימה. הגרעינים שבמקור הפולטים את קרני הגמא חייבים להיות מאותו איזוטופ כמו הגרעינים בדגימה הקולטת אותם.
כמוסבר לעיל, אם הגרעינים הפולטים והבולעים היו בסביבות כימיות זהות, אנרגיות המעבר הגרעיניות היו שוות בדיוק וחלק ניכר מהקרינה הייתה נבלעת בתהודה. במקרה המורכב יותר, ההבדל בסביבות הכימיות בין הסריגים, גורם לרמות האנרגיה הגרעיניות להשתנות בכמה דרכים שונות, כמתואר להלן. אף על פי ששינויי האנרגיה הללו הם זעירים (לעיתים קרובות פחות ממיקרו אלקטרון וולט), הרוחב הטבעי הצר של קרינת הגמא מונעת מהקרינה הנפלטת להיקלט בתהודה בסריג המטרה. כדי לגרום למצב בו כן מתקיימת תהודה בקליטת קרינת הגמא, נעשה שימוש בהסטת דופל.
במהלך ספקטרוסקופיית קליטה של מסבאואר, המקור מואץ בטווח מהירויות באמצעות מנוע ליניארי כדי לייצר אפקט דופלר ולמצוא באיזה מהירויות של המקור מתבצעת בליעה של קרני הגמא במטרה. טווח אופייני של מהירויות עבור ברזל-57, למשל, עשוי להיות ±11 מ"מ\שנייה (עבור ברזל-57 הזזה במהירות של 1 מ"מ\שנייה תוביל לשינוי של כ-50 ננו אלקטרון וולט באנרגיה של קרינת הגמא).[2]
בספקטרום המתקבל, עוצמת קרינת הגמא בגלאי שמוצב מאחורי המטרה משורטטת כפונקציה של מהירות המקור. במהירויות שמתאימות לרמות האנרגיה התהודה של הדגימה, נספגים חלק גדול של קרני הגמא ביחס למהירויות בהם קרינת הגמא לא נספגת בתהודה. כתוצאה מכך, ניתן לראות במהירויות אלה ירידה בעוצמה הקרינה הנמדדת בגלאי, המתאפיינת בירידה מתאימה בספקטרום. מספר המקומות בהן קיימת ירידה כזו, המיקומים של הירידות והעוצמה שלהן (כלומר כמות הקרינה הנבלעת) מספקים מידע על הסביבה הכימית של הגרעינים במטרה וניתן להשתמש בהם כדי לאפיין את הדגימה.
בחירת מקור מתאים
מקורות קרני גמא מתאימים מורכבים מגרעין רדיואקטיבי שמתפרק לאיזוטופ רצוי שלאחר מכן דועך לרמת היסוד הגרעיני באמצעות פליטת קרינת גמא. לדוגמה, המקור לספקטרוסקופייה באמצעות ברזל-57 הוא קובלט-57, שמתפרק על ידי לכידת אלקטרון למצב מעורר של ברזל-57, אשר בתורו דועך למצב היסוד באמצעות סדרה של פליטות קרני גמא הכוללות את זו בה חלק ניכר מהגרעינים פולטים קרינה ללא רתע ובה נעשה שימוש בספקטרוסקופיית מסבאואר. באופן אידיאלי לאיזוטופ הראשוני יהיה זמן מחצית חיים נוח, כלומר לא קצר מדי, שידעך באופן מהיר וידרוש תחלופה קבועה של המקור, ולא ארוך מדי שיספק שטף נמוך מדי של קרינת גמא. לדוגמה, זמן מחצית החיים של קובלט-57 הוא 270 ימים. כמו כן, אנרגיית קרני הגמא צריכה להיות נמוכה יחסית, אחרת רוב הפליטות בסריג יהיו עם רתיעה וכתוצאה מכך יחס אות לרעש בספקטרוסקופייה יהיה נמוך והספקטרוסקופיה תדרוש זמני איסוף ארוכים. שיקולים אלו גורמים לכך שברזל-57 הוא האלמנט הנפוץ ביותר המשמש בספקטרוסקופיה, אם כי נעשה שימוש באופן יחסית שכיח גם ביוד-129, בדיל-119 ואנטימון-121.
ניתוח ספקטרום של ספקטרופיית מסבאואר
כפי שתואר לעיל, לספקטרוסקופיית מסבאואר יש רזולוציית אנרגיה עדינה ביותר והיא יכולה לזהות אפילו שינויים עדינים בסביבה הגרעינית של האטומים הרלוונטיים. בדרך כלל, ישנם שלושה סוגים של אינטראקציות המשפיעות על רמות האנרגיה הגרעיניות שנצפים: הסטה איזומרית, פיצול קוודרופול ופיצול מגנטי על-דק.[3]
הסטה איזומרית
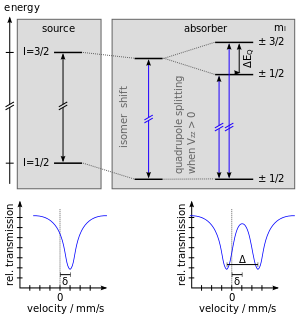
הסטה איזומרית (δ) (נקראת לפעמים גם הסטה כימית, במיוחד בספרות הישנה יותר) היא מדד יחסי המתאר שינוי לא זהה בהפרשי האנרגיות הפנימיות של הגרעין (ולכן שינוי באנרגיית המעבר) (ראה איור 2) עקב ההשפעה של האלקטרונים באטום. האלקטרונים באורביטל s, יכולים בסיכוי מסוים לחפוף את הגרעין. החפיפה בין מיקומי האלקטרונים לגרעין משנה את רמות האנרגיה של הגרעין עצמו כתוצאה מהאינטראקציה החשמלית בין הגרעין לאלקטרונים. מאחר שהגרעין במצב המעורר הוא בעל נפח שונה מהגרעין במצב היסוד, השינוי באנרגיה של מצב היסוד לא זהה להשינוי באנרגיה של המצב המעורר, ולכן אנרגיית המעבר בין המצבים משתנה בהתאם לצפיפות האלקטרונים באורביטל s באזור הגרעין.
רק לאלקטרונים באורביטלים s יש הסתברות שאינה אפס להימצא בגרעין (ראה אורביטלים אטומיים). עם זאת, אלקטרונים באורביטלים p, d ו-f משפיעים על צפיפות האלקטרונים באורביטל s באמצעות אפקט מיסוך.
את ההסטה האיזומרית ניתן לבטא באמצעות הנוסחה:
כאשר K הוא קבוע גרעיני (כלומר הערך של K זהה בכל מצב בו העשה שימוש בברזל-57, אך עבור איזוטופ אחר כדוגמת יוד-129 יהיה ערך שונה ל-K), הוא הרדיוס האפקטיבי של הגרעין במצב המעורר ו- הוא הרדיוס במצב היסוד. הוא הסיכוי למצוא אלקטרון בקרבת הגרעין בסריג שפולט את הקרינה ו- הוא הסיכוי למצוא אלקטרון כזה בסריג שקולט אותה.
כדי להבהיר את המשמעות הפיזיקלית של משוואה זו נראה שתי דוגמאות:
- עלייה בסיכוי למצוא אלקטרונים באורביטל s בספקטרום של ברזל-57 נותנת תזוזה שלילית כיוון שהשינוי במטען הגרעיני האפקטיבי הוא שלילי (עקב ), עלייה בצפיפות האלקטרונים הללו בבדיל-119 מוביח להסטת איזומרים חיובית (כי עבור בדיל ).
- ליוני ברזל מחומצנים (Fe 3+) יש הזזות איזומריות נמוכות יותר מאשר ליוני ברזל (Fe 2+) מכיוון שצפיפות האלקטרונים באורביטל ה-s באזור הגרעין של יוני ברזל גדולה מהצפיפות ביוני ברזל מחומצנים עקב אפקט מיסוך חלש יותר על ידי אלקטרונים באורביטל d.[4]
ההיסט האיזומרי כפי שמתואר כאן אינו משתנה עם הטמפרטורה, עם זאת, לספקטרום מסבאואר יש רגישות לטמפרטורה עקב אפקט יחסי המכונה אפקט דופלר מסדר שני. ככלל, השפעה זו קטנה, ותקן IUPAC מאפשר לדווח על היסט האיזומר מבלי לתקן עבורה.[5]
הסטת האיזומר שימושית לקביעת מצב חמצון ועוד.[3]
פיצול קוודרופול

פיצול קוודרופול משקף את האינטראקציה בין רמות האנרגיה הגרעינית לבין גרדיאנט השדה החשמלי מסביב לגרעין. גרעינים במצבים עם התפלגות מטען לא כדורית, כלומר כל אלה עם מספר ספין קוונטי (I) גדול מ-1/2, עשויים להיות בעלי מומנט קוודרופול גרעיני. במקרה זה שדה חשמלי א-סימטרי (המיוצר על ידי חלוקת מטען אלקטרוני א-סימטרי) מפצל את רמות האנרגיה הגרעינית.[3]
במקרה של איזוטופ עם מצב מעורר בו המספר הקוונטי הוא I=3/2, כגון ברזל-57 או בדיל-119, המצב המעורר מפוצל לשני מצבי משנה mI=±1/2 ו-mI=±3/2. המעבר האטומי ממצב היסוד למצבים המעוררים מופיע כשתי פסגות ספציפיות בספקטרום, המכונה לפעמים "דאבלט". פיצול קוודרופול נמדד כהפרדה בין שתי הפסגות הללו ומשקף את אופי השדה החשמלי בגרעין.
ניתן להשתמש בפיצול הקוודרופול לקביעת מצב החמצון, מצב הספין, סימטריית האתר וסידור הליגנדים.[3]

פיצול מגנטי על-דק
פיצול על-דק מגנטי הוא תוצאה של האינטראקציה בין הגרעין לבין שדה מגנטי מסביבו, כפי שמתואר על ידי אפקט זימן הגרעיני (להבדיל מאפקט זימן הרגיל המתאר פיצול של רמות האנרגיה של האטום כתוצאה משדה מגנטי). גרעין עם ספין I מתפצל ל-2I+1 רמות אנרגיה בנוכחות שדה מגנטי. לדוגמה, המצב המעורר הראשון של גרעין ברזל-57 עם מצב ספין I=3/2 יתפצל ל-4 תת-מצבים לא מנוונים עם ערכי mI של +3/2, +1/2, -1/2 ו--3/2. הפרש האנרגיה בין המצבים הללו הוא אחיד, והפיצול נקרא פיצול על-דק, סדר הגודל של הפרשי האנרגיה הוא מאות ננו אלקטרו וולט. כלל הבחירה למעברים מגנטיים, אומר שמעברים בין המצב המעורר למצב היסוד יכולים להתרחש רק כאשר המספר הקוונטי mI משתנה ב-0 או 1 או -1. כלל זה מאפשר שישה מעברים בעלי אנרגיות שונות בין רמת אנרגי של I=1/2 לרמת אנרגיה של I=3/2. ספקטרום לדוגמה של פיצול על-דק מוצג באיור 4.[3]
מידת הפיצול היא פרופורציונלית לחוזק השדה המגנטי בגרעין, אשר בתורו תלוי בחלוקת האלקטרונים ("סביבה כימית") של האטום. ניתן לקבוע את השדה המגנטי מהמרווח בין הפסגות המומנטים המגנטיים של המצבים השונים. בחומרים פרומגנטיים, כולל תרכובות ברזל רבות, השדות המגנטיים הפנימיים הטבעיים חזקים למדי והשפעותיהם שולטות בספקטרום.
שילוב של שלושת הפרמטרים
פעמים רבות כל ההשפעות - הסטת איזומר, פיצול קוודרפולי, ואפקט זימן מגנטי - קיימות בדגימה ונצפות בספקטרוסקופיה. במקרים כאלה ההיסט האיזומרי נקבע על ידי הממוצע של כל הקווים. הפיצול הקוודרופולי ניתן על ידי ההזזה של שני הקווים החיצוניים ביחס לארבעת הקווים הפנימיים (ארבעת הקווים הפנימיים מתאימים למצב בו mI=1/2,-1/2 במצב המעורר בעוד הקווים החיצוניים מתאימים למצבים בהם mI=3/2,-3/2, לכן הפיצול הקוודרפולי יוצר הבדל בין הקווים החיצוניים לפנימיים). והאפקט העל-דק נמדד מהקווים הפנימיים. בדרך כלל נעשה שימוש בתוכנת התאמה לערכים מדויקים.
בספקטרום המתקבל בספקטרוסקופיית מסבאואר, גם כאשר הספקטרום כולל את שלושת הפרמטרים של מסבאואר, ניתן להשתמש לעיתים קרובות כדי לזהות תרכובת מסוימת על ידי השוואת ההסטה האיזומרית, הפיצול הקוודרופולי והפיצול העל-דק שהתקבלו עבור דגימה מסוימת לערכים אלו שהתקבלו בעבר עבור דגימה ידועה.[6]
במקרים מסוימים, לתרכובת עשויה להיות יותר ממיקום אפשרי אחד עבור האטום הפעיל של מסבאואר. לדוגמה, מבנה הגביש של מגנטיט (Fe3O4) תומך בשני אתרים שונים עבור אטומי הברזל. ולכן לספקטרום שלו 12 פסגות, שש פסגות לכל אתר אטומי אפשרי, כאשר כל שישייה כזו מתאימה לקבוצות של פרמטרים של מסבאואר.
בנוסף, העוצמות היחסיות של הפסגות השונות משקפות את הריכוזים היחסיים של תרכובות בדגימה וניתן להשתמש בהן לניתוח חצי כמותי. כמו כן, מכיוון שתופעות פרומגנטיות תלויות בגודל, במקרים מסוימים ספקטרה יכולה לספק תובנה לגבי גודל הגביש ומבנה הגרגירים של חומר.
יישומים
בין החסרונות של הטכניקה ניתן למנות את המספר המצומצם של מקורות קרני גמא והדרישה שהדגימות יהיו מוצקות על מנת למנוע את הרתיעה של הגרעין. היתרונות של ספקטרוסקופיית מסבאואר נובעות מהרגישות שלה לשינויים עדינים בסביבה הכימית של הגרעין לרבות שינויים במצב חמצון, השפעת הליגנדים השונים על אטום מסוים והסביבה המגנטית של הדגימה.
ככלי אנליטי ספקטרוסקופיית מסבאואר הייתה שימושית במיוחד בתחום הגאולוגיה לזיהוי הרכב של דגימות המכילות ברזל כולל מטאוריטים וסלעי ירח. איסוף נתונים של ספקטרום מסבאואר בוצע גם על סלעים עשירים בברזל על מאדים, בתוכנית מארס רובר.[7]
ביישום אחר, ספקטרוסקופיית מסבאואר משמשת לאפיון מעברי פאזה בזרזי ברזל, למשל, אלו המשמשים לסינתזה של פישר-טרופש (אנ': Fischer-Tropsch_process). בעוד שהם מורכבים בתחילה מהמטיט (Fe2O3), זרזים אלה הופכים לתערובת של מגנטיט (Fe3O4) ומספר קרבידים של ברזל. השינוי בסביבה הכימית של אטומי הברזל יכול להימדד באמצעות ספקטרוסקופיית מסבאואר.[8]
ספקטרוסקופיית מסבאואר שימשה גם כדי לקבוע את שינוי הריכוז היחסי במצב החמצון של אנטימון (Sb) במהלך החמצון הסלקטיבי של אולפינים. במהלך ההסתיידות, כל יוני האנטימון בזרז פח דו-חמצני המכיל אנטימון הופכים למצב חמצון +5. בעקבות התגובה הקטליטית, כמעט כל היונים חוזרים ממצב החמצון +5 ל-+3. שינוי משמעותי בסביבה הכימית הסובבת את גרעין האנטימון מתרחש במהלך השינוי במצב החמצון, אשר ניתן לנטר בקלות כשינוי בהסטת האיזומר בספקטרום מסבאואר.
טכניקה זו שימשה גם כדי לצפות באפקט דופלר רוחבי מסדר שני שנחזה על ידי תורת היחסות, שימוש שהתאפשר באמצעות רזולוציית אנרגיה גבוהה מאוד.[9]
כימיה ביו-אורגנית
ספקטרוסקופיית מסבאואר מיושמת באופן נרחב בכימיה ביו-אורגנית, במיוחד לחקר חלבונים ואנזימים המכילים ברזל. לעיתים קרובות הטכניקה משמשת כדי לקבוע את מצב החמצון של ברזל. דוגמאות לביו-מולקולות בולטות המכילות ברזל הן חלבוני ברזל-גופרית, פריטין, הם כולל ציטוכרומים. מחקרים אלה מתווספים לעיתים קרובות על ידי ניתוח של מתחמי מודל קשורים.[10][11] תחום המושך עניין הוא אפיון של תוצרי ביניים המעורבים בהפעלת חמצן על ידי חלבוני ברזל.
ספקטרומטר מסבאואר
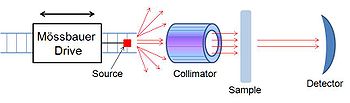
ספקטרומטר מסבאואר הוא מכשיר המבצע ספקטרוסקופיית מסבאואר, או מכשיר המשתמש באפקט מסבאואר כדי לקבוע את הסביבה הכימית של גרעינים המקיימים אפקט מסבאואר שנמצאים בדגימה. הספקטרומטר מכיל שלושה חלקים עיקריים; מקור שזז קדימה ואחורה כדי ליצור אפקט דופלר, קולימטור המסנן קרני גמא לא מקבילות וגלאי.
ספקטרומטר מסבאואר מיניאטורי, בשם (MB) MIMOS II, שימש את שני הרוברים במשימות מארס רובר של נאס"א.[12]
הערות שוליים
- ↑ International Board on the Applications of the Mössbauer Effect (IBAME) and Mössbauer Effect Data Center (MEDC), Mössbauer Effect website Accessed June 3, 2010.
- ↑ Mössbauer Spectroscopy Group, Royal Society of Chemistry (RSC) website, Introduction to Mössbauer Spectroscopy Part 1 Accessed June 3, 2010
- ^ 3.0 3.1 3.2 3.3 3.4 Mössbauer Spectroscopy Group, Royal Society of Chemistry (RSC) website, Introduction to Mössbauer Spectroscopy Part 2 Accessed June 3, 2010.
- ↑ Walker, L.; Wertheim, G.; Jaccarino, V. (1961). "Interpretation of the Fe57 Isomer Shift". Physical Review Letters. 6 (3): 98. Bibcode:1961PhRvL...6...98W. doi:10.1103/PhysRevLett.6.98.
- ↑ International Board on the Applications of the Mössbauer Effect (IBAME) and Mössbauer Effect Data Center (MEDC), Mössbauer Effect website Accessed December 20, 2017
- ↑ Mössbauer Effect Data Center.
- ↑ Schröder, Christian (2015). "Mössbauer spectroscopy in astrobiology". Spectroscopy Europe. 27 (2): 10. נבדק ב-2018-01-08.
- ↑ Sarkar, A.; et al. (2007). "Fischer–Tropsch Synthesis: Characterization Rb Promoted Iron Catalyst". Catalysis Letters. 121 (1–2): 1–11. doi:10.1007/s10562-007-9288-1.
- ↑ Chen, Y.-L.; Yang, D.-P. (2007). "Recoilless Fraction and Second-Order Doppler Effect". Mössbauer Effect in Lattice Dynamics. John Wiley & Sons. doi:10.1002/9783527611423.ch5. ISBN 978-3-527-61142-3.
- ↑ Martinho, Marlène; Münck, Eckard (2010). "57Fe Mössbauer Spectroscopy in Chemistry and Biology". Physical Inorganic Chemistry. pp. 39–67. doi:10.1002/9780470602539.ch2. ISBN 9780470602539.
- ↑ Schuenemann, V.; Paulsen, H. (2007-12-10). "Moessbauer spectroscopy". In Scott, Robert A.; Lukehart, Charles M. (eds.). Applications of Physical Methods to Inorganic and Bioinorganic Chemistry. ISBN 978-0-470-03217-6.
- ↑ Klingelhöfer, G.; et al. (2002). "The miniaturized Mössbauer spectrometer MIMOS II for extraterrestrial and outdoor terrestrial applications: A status report". Hyperfine Interactions. 144 (1–4): 371–379. Bibcode:2002HyInt.144..371K. doi:10.1023/A:1025444209059.
קישורים חיצוניים
ספקטרוסקופיית מסבאואר41459448Q899927


