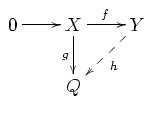מודול אינג'קטיבי

בתורת החוגים, מודול אינג'קטיבי הוא מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} מעל חוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} , כך שלכל מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} ותת-מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} , כל הומומורפיזם מ-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} ניתן להרחבה כך שיהיה מוגדר על כל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} . הדוגמה הקלאסית למודול כזה היא אוסף המספרים הרציונליים $\mathbb {Q}$ מעל חוג המספרים השלמים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{Z}} .

חשיבותם של המודולים האלה נובעת בעיקר מכך שמבחינה קטגורית, מושגי האינג'טיביות והפרויקטיביות של מודולים דואליים זה לזה.

לצד הקשר ההדוק שיש למודולים אינג'קטיביים עם חוג המקדמים (המתבטא למשל בכך שכל מודול אינג'קטיבי הוא בפרט חליק), כל מודול מוכל במודול אינג'קטיבי מינימלי, הנקרא "הסגור האינג'קטיבי" שלו.

את התכונה אפשר להגדיר בכל קטגוריה (לאו דווקא של מודולים). עם זאת, לא בכל קטגוריה קיימים אובייקטים אינג'קטיביים. לדוגמה, בקטגוריה של חבורות רק החבורה הטריוויאלית היא אינג'קטיבית [1].

הגדרה

מודול שמאלי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} מעל חוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} הוא אינג'קטיבי אם הוא מקיים אחד התנאים השקולים הבאים:

• כל סדרה מדויקת מהצורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \longrightarrow Q \longrightarrow M \longrightarrow N \longrightarrow 0} מתפצלת.
• לכל מודול שמאלי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} , אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} הוא תת-מודול של $M$ אז הוא מחובר ישר של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} , כלומר קיים ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} תת-מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} כך ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q\oplus N = M} .
• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} אינו תת-מודול גדול באף מודול.
• עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} מודולים שמאליים $X$ ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} ופונקציה חח"ע הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f:X\rightarrow Y} , כל פונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle g:X\rightarrow Q} ניתנת להרחבה ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} , כלומר קיימת פונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle h:Y\rightarrow Q} כך ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle h \circ f = g} . לחלופין, אם השורה העליונה בדיאגרמה הבאה מדויקת, אז ניתן למצוא פונקציה $h$ כך שהדיאגרמה תהיה קומוטטיבית

• קריטריון Baer: בהגדרה לעיל מספיק להניח ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} הוא החוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} , ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} אידיאל שמאלי שלו.
• הפונקטור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \operatorname{Hom}(-,Q)} מקטגוריית ה-$R$ מודולים השמאליים לקטגוריית החבורות האבליות הוא פונקטור מדויק.

מודול אינג'טיבי ימני מוגדר באופן אנלוגי.

דוגמאות ותכונות

מודול האפס תמיד אינג'קטיבי. מכפלה ישרה של מודולים אינג'קטיביים היא אינג'קטיבית. מחובר ישר במודול אינג'קטיבי הוא אינג'קטיבי.

מעל שדה כל מודול הוא אינג'קטיבי, כפי שאפשר להוכיח על ידי השלמת בסיס לתת-מודול לבסיס של המודול כולו. המודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{Q}} של המספרים הרציונליים מעל החוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{Z}} של השלמים הוא אינג'קטיבי. גם מודול המנה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{Q}/ \mathbb{Z}} הוא אינג'טיבי.

מעל חוג דדקינד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} , לכל אידיאל ראשוני $P$ (שאינו אפס), הגבול הישר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_P = \lim_{\rightarrow} R/P^n} הוא מודול אינג'קטיבי אי-פריד (indecomposable), וכל מודול אינג'קטיבי אי-פריד הוא כזה. לפי משפט Matlis (1958), מעל כל חוג קומוטטיבי נתרי יש התאמה בין אידיאלים ראשוניים למודולים אינג'קטיביים אי-פרידים. אפילו כאשר החוג לא קומוטטיבי, לכל מודול אינג'קטיבי אי-פריד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} אפשר להתאים ראשוני באופן הבא: הראשוני הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} מתאים ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} אם יש ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} תת-מודול $N$, כך ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} הוא המאפס של כל תת-מודול שונה מאפס של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} .

חליקות

מודול שמאלי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} הוא חליק אם לכל סקלר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} בחוג ולכל וקטור $m$, התכונה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ ar = 0 \implies am = 0} שקולה ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ m \in r M} . כל מודול אינג'קטיבי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} הוא חליק. מעל מחלקות מסוימות של חוגים, כגון מעל תחומי שלמות או באופן כללי יותר מעל כל תת-חוג של חוג עם חילוק, כל מודול חסר פיתול חליק הוא אינג'קטיבי. מעל תחום אידיאלים שמאליים ראשי (PLID), כל מודול חליק הוא אינג'קטיבי.

הסגור האינג'קטיבי

כל מודול מעל חוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} ניתן לשיכון במכפלה ישרה של עותקים של המודול האינג'קטיבי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \operatorname{Hom}(R,\mathbb{Q}/\mathbb{Z})} .

התכונות הבאות שקולות עבור מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} המוכל במודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} :

• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} הוא תת-מודול גדול של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} , אבל לא של אף מודול המכיל את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} ;
• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} הוא תת-מודול גדול של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} , ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} אינג'קטיבי;
• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} אינג'קטיבי ואין לו אף תת-מודול אינג'קטיבי המכיל את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} .

סגור אינג'קטיבי (injective hull) של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} הוא מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} המקיים את התכונות לעיל. לכל מודול יש סגור אינג'קטיבי יחיד. לדוגמה, הסגור האינג'קטיבי של השלמים (כמודול מעל עצמם) הוא מודול המספרים הרציונליים. הסגור האינג'קטיבי של חוג המטריצות 2x2 המשולשיות-עליונות מעל חוג עם חילוק הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} , הוא חוג כל המטריצות בגודל זה מעל החוג. הסגור האינג'קטיבי של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R/P} , כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} חוג דדקינד ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} ראשוני, הוא המודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_P} שהוגדר לעיל.

אפיון תכונות של חוגים באמצעות מודולים אינג'קטיביים

כל המודולים מעל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} אינג'קטיביים אם ורק אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} חוג פשוט למחצה ארטיני (כלומר, סכום ישר סופי של מטריצות מעל חוגי חילוק); לשם כך מספיק שכל המודולים הציקליים מעל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} יהיו אינג'קטיביים (Osofsky).

סכום ישר סופי של מודולים אינג'קטיביים הוא אינג'קטיבי, אבל טענה זו אינה נכונה לסכום ישר כלשהו. תכונה זו מתקיימת (למודולים שמאליים) אם ורק אם החוג נתרי (שמאלי). בדומה לזה, כל מודול אינג'קטיבי מתפרק לסכום ישר של מודולים אי-פריקים אם ורק אם החוג נתרי. כל מודול אינג'קטיבי מתפרק לסכום ישר של סגורים אינג'קטיביים של מודולים פשוטים, אם ורק אם החוג ארטיני.

באופן כללי תמונה הומומורפית של מודול אינג'קטיבי אינה בהכרח אינג'קטיבית. תכונה זו מתקיימת אם ורק אם החוג תורשתי. לכל מודול יש תת-מודול אינג'קטיבי גדול ביותר, אם ורק אם החוג תורשתי ונתרי.

חוג נקרא אינג'קטיבי לעצמו (self injective) אם הוא אינג'קטיבי כמודול מעל עצמו. כל מודול אינג'קטיבי הוא פרויקטיבי, אם ורק אם כל מודול פרויקטיבי הוא אינג'קטיבי, אם ורק אם החוג אינג'קטיבי לעצמו מימין ומשמאל וארטיני (חוג כזה נקרא חוג קוואזי-פרובניוס).

חוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} נקרא לא-סינגולרי (שמאלי) אם לכל איבר שונה מאפס הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} יש איבר שונה מאפס הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , כך שאם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle ayx=0} אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle ay=0} . כל חוג כזה משוכן בחוג רגולרי פון-נוימן (החוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{End}(Q)} כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} הסגור האינג'קטיבי של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} כמודול מעל עצמו). חוג לא-סינגולרי שהוא אינג'קטיבי לעצמו (שמאלי) הוא בעצמו רגולרי פון-נוימן.

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} חוג קומוטטיבי, כל המודולים הפשוטים שלו אינג'קטיביים אם ורק אם הוא רגולרי פון-נוימן.

גרסאות חלשות של אינג'קטיביות

מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} הוא קוואזי-אינג'קטיבי, אם לכל תת-מודול שלו, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} , כל הומומורפיזם מ-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} ניתן להרחבה כך שיהיה מוגדר על כל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} . כל מודול אינג'קטיבי הוא קוואזי-אינג'קטיבי, אבל ההפך אינו נכון (החבורה הציקלית מסדר 4 קוואזי-אינג'קטיבית אבל לא אינג'קטיבית). כל מודול פשוט-למחצה הוא קוואזי-אינג'קטיבי. מודול הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} קוואזי-אינג'קטיבי אם ורק אם הוא אינווריאנטי לחלוטין בסגור האינג'קטיבי שלו (כלומר, כל אנדומורפיזם של הסגור האינג'קטיבי נושא את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} לעצמו). אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \oplus B} קוואזי-אינג'קטיבי אז גם המחוברים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B} כאלה (אבל ההפך אינו בהכרח נכון). למודולים קוואזי-אינג'קטיביים יש חוג אנדומורפיזמים מעניין: רדיקל ג'ייקובסון שלו כולל את האנדומורפיזמים שהגרעין שלהם עיקרי, וחוג המנה ביחס אליו הוא רגולרי, אינג'קטיבי לעצמו, ואפשר להרים ממנו מערכות בנות-מניה של אידמפוטנטים אורתוגונליים בחזרה אל חוג האנדומורפיזמים. למודול קוואזי-אינג'קטיבי אי-פריק יש חוג אנדומורפיזמים מקומי יוניפורמי (היינו כל שני אידיאלים שמאליים שונים מאפס - נחתכים). חוג האנדומורפיזמים של מודול קוואזי-אינג'קטיבי ולא-סינגולרי הוא רגולרי ואינג'קטיבי לעצמו.

מודול הוא skew-injective אם כל אנדומורפיזם של תת-מודול שלו, ניתן להרחבה לאנדומורפיזם של המודול כולו. כל מודול קוואזי-איג'קטיבי הוא skew-injective, וההפך נכון עבור מודולים ארטיניים למחצה (מודול הוא ארטיני למחצה אם לכל מנה לא טריוויאלית שלו יש תת-מודול עיקרי שהוא פשוט למחצה).

תכונה חלשה עוד יותר נקראת הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} -אינג'קטיביות. מודול הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} -אינג'קטיבי אם כל אנדומורפיזם אידמפוטנטי של תת-מודול שלו, ניתן להרחבה לאנדומורפיזם של המודול כולו. בחבורות אבליות, תכונה זו שקולה ל-skew-injectiveness. מודול הוא יוניפורמי (כל שני תת-מודולים שונים מאפס - נחתכים) אם ורק אם הוא אי-פריק ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} -אינג'קטיבי. מעל חוג נתרי, כל מודול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} -אינג'קטיבי הוא סכום ישר של מודולים יוניפורמיים. אם כל מודול מעל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} הנוצר על ידי שני איברים הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} -אינג'קטיבי, אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} פשוט למחצה ארטיני. אם כל מודול ציקלי מעל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} -אינג'קטיבי, אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} הוא מכפלה ישרה של חוג פשוט למחצה ארטיני, וחוג יוניפורמי.

לקריאה נוספת

• Joseph J. Rotman, An Introduction to Homological Algebra
• The Concise Handbook of Algebra, C.21: Injective Modules, A.A.Tuganbaev.

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

מודול אינג'קטיבי32650419Q2716519