טנזור מאמצים

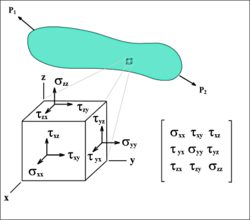
טנזור המאמצים

טנזור המאמצים בתיאור אינדקסים כללי

טנזור המאמצים (נקרא גם טנזור המאמצים של קושי, על שם אוגוסטן לואי קושי) מתאר את המאמצים על פני קובייה קטנה של החומר הנתון בעומס חיצוני, שנהוג לייצגו על ידי מטריצה בת תשעה רכיבים (3 על 3). טנזור המאמצים מרכז את מאמצי המתיחה, הלחיצה והגזירה, הפועלים על נקודה חומרית בגוף. טנזור המאמצים מקשר בין וקטור כיוון באורך יחידה e לווקטור גרירה T^(e) הפועל על מישור דמיוני הניצב ל-e:

${\mathbf{𝐓}}^{(\mathbf{𝐞})}=\mathbf{𝐞}\cdot \mathit{\sigma }\text{or}{T}_j^{(e)}=\sum _i{\sigma }_{ij}{e}_i.$

מילולית, האיבר ${\sigma }_{ij}$ בטנזור מייצג את המאמץ המופעל בכיוון ציר j על פאה שהניצב לה מקביל לכיוון ציר i. אם i=j (איבר על האלכסון הראשי) אז הווקטור הניצב לפאה וכיוון הכוח מתלכדים, ולכן זהו מאמץ נורמלי או מאמץ לחיצה/מתיחה. אם i שונה מ-j האיבר ${\sigma }_{ij}$ מייצג כוח הפועל על פאה במקביל אליה, ולכן מייצג מאמץ גזירה. לפי עקרון שימור התנע הזוויתי, על מנת שקובייה תימצא במנח קבוע במרחב צריך להתקיים שסכום המומנטים הפועלים עליה ביחס לנקודה שרירותית יהיה אפס, מה שמוביל למסקנה שטנזור המאמצים סימטרי, ולפיכך יש לו ששה רכיבי מאמץ בלתי תלויים, במקום תשעת המקוריים.

על מנת שהקובייה תימצא בשיווי משקל מכני (כלומר בעלת תאוצה קווית אפס) דרוש תנאי נוסף על ההשתנות המרחבית של טנזור המאמצים, המגלם את התנאי ששקול הכוחות מתאפס. פורמלית, התנאי קובע ש-$\mathrm{\nabla }\cdot \sigma +{\overrightarrow{F}}_{ext}=0$, כאשר${\overrightarrow{F}}_{ext}$ הוא שקול הכוחות החיצוניים ליחידת נפח, הפועלים על הקובייה. למשל, בגזירת משוואת שיווי המשקל ההידרוסטטי הכוח החיצוני הרלוונטי הוא כוח הכבידה.

טנזור המאמצים של קושי משמש בניתוח מאמצים גופים חומריים הנתונים למעוותים קטנים; זהו מושג מפתח בתאוריית האלסטיות הליניאריות. עבור מעוותים גדולים יותר, המכונים גם מעוותים סופיים, מדדים מורכבים יותר נדרשים.

טנזור המאמצים

$T=\left(\begin{array}{ccc}{\sigma }_{xx}& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_{yy}& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_{zz}\\ \end{array}\right)$

משווי משקל מקבלים מטריצה סימטרית ובה 6 רכיבים שונים. מתקיים השוויון בין הרכיבים:

• ${\tau }_{xy}={\tau }_{yx}$
• ${\tau }_{zx}={\tau }_{xz}$
• ${\tau }_{zy}={\tau }_{yz}$

לכן:

$T=\left(\begin{array}{ccc}{\sigma }_{xx}& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{xy}& {\sigma }_{yy}& {\tau }_{yz}\\ {\tau }_{xz}& {\tau }_{yz}& {\sigma }_{zz}\\ \end{array}\right)$

טנזור המאמצים הוא טנזור סימטרי ותמיד אפשר להציג אותו כסכום של שני טנזורים סימטריים שהם:

• טנזור ממוצע או מאמצים הידרוסטטי הכולל מאמצי מתיחה או לחיצה בלבד
• טנזור מאמצי גזירה הכולל מאמצי גזירה בלבד.

תיאור כללי

התיאור הכללי של טנזור המאמצים נעשה באמצעות אינדקסים 1,2,3

x	→	1
y	→	2
z	→	3
σxx	→	σ11
τxy	→	σ12
τxz	→	σ13
...

ונקבל:

$T=\left(\begin{array}{ccc}{\sigma }_{11}& {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_{22}& {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_{33}\\ \end{array}\right)$

את חוק הוק אפשר להציג באמצעות המינוח הזה של האינדקסים בצורה הבאה:

${\sigma }_{ij}=\sum _{kl}{C}_{ijkl}\cdot {\epsilon }_{kl}$

תורת היחסות

טנזור מאמץ-אנרגיה יחסותי ורכיביו

בתורת היחסות טנזור המאמצים הוא חלק מטנזור 4 על 4 הנקרא טנזור צפיפות האנרגיה או טנזור המאמץ-אנרגיה ומסומן $T_{\mu \nu }$ (כאשר $\mu ,\nu =ct,x,y,z=0,1,2,3$): זהו טנזור סימטרי שכולל את צפיפות האנרגיה, שטף האנרגיה, תנע ואת טנזור מאמצים (תת-מערך בגודל 3 על 3). טנזור זה מופיע במשוואת השדה של איינשטיין $G_{\mu \nu }=\frac{8\pi G}{c^4}{T}_{\mu \nu }$ (כאשר $G_{\mu \nu }$ הוא טנזור איינשטיין) המתארת את עקמומיות המרחב-זמן כתלות בהתפלגות צפיפות האנרגיה, המסה, התנע והלחץ במרחב-זמן.

ראו גם

• מאמץ (הנדסה)

לקריאה נוספת

• Timoshenko S.P, Strength of Materials, 3rd edition, Krieger Publishing Company, 1976. מסת"ב 0882754203
• S.P. Timoshenkoo & J.N. Goodier Theory of Elasticity, 3rd edition, International Student Edition, McGraw-Hill 1970..
• Shames I.H., Cozzarelli F.A., Elastic and inelastic stress analysis, Prentice-Hall, 1991, מסת"ב 1560326867
• Love, A. E. H. (4 ed.). (1944). Treatise on the Mathematical Theory of Elasticity. Dover Publications. מסת"ב 0486601749.
• Marsden, J. E., & Hughes, T. J. R. (1994). Mathematical Foundations of Elasticity. Dover Publications. מסת"ב 0486678652.

---

קישורים חיצוניים

מדיה וקבצים בנושא טנזור מאמצים בוויקישיתוף

• מאמצים וטנזור מאמצים, באנגלית
• טנזור המאמצים, באנגלית

ערך זה הוא קצרמר בנושא פיזיקה. אתם מוזמנים לתרום למכלול ולהרחיב אותו.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

טנזור מאמצים41618243Q13409892