חידת בור

חידת בור (או "פאזל בור" Burr Puzzle) היא חידה מכנית מסוג חידת שילובים המורכבת ממוטות מחורצים, אשר משתלבים ליחידה תלת ממדית, בדרך כלל סימטרית. לרוב עשויות חידות אלו מעץ, אך ניתן למצוא גם גרסאות מפלסטיק או מתכת. בשנים האחרונות התרחבה הגדרה זו וממציאי חידות נוהגים לקרוא "בור" גם לחידות המורכבות מחלקים שאינם מוטות בלבד.
השם "בור" מופיע לראשונה בספרו של אדווין וויאט משנת 1928[1], אך מהכתוב נראה כי כינוי זה היה בשימוש עוד לפני כן. הכינוי מיוחס לצורתן של החידות כשהן מורכבות, אשר יכול להזכיר את סוג הזרעים הנקראים כך באנגלית.
מקורן של חידות הבור אינו ידוע, אך עדות ראשונה להן[2] מופיעה בתחריט משנת 1698 המשמש כדף הפתיחה של ציקלופדיית צ'יימברס. עדויות מאוחרות יותר ניתן למצוא בקטלוגים גרמניים מסוף המאה ה-18 ותחילת המאה ה-19.[3] יש הטוענים שייתכן כי הבור הוא המצאה סינית, כמו חידות קלאסיות אחרות כגון הטנגרם.[4] הפטנט הראשון המציג חידה מסוג זה הוא משנת 1917.[5]
בור 6 חלקים

"בור 6 חלקים", הנקרא לעיתים גם "חידת הלולאה" או "הצלב הסיני", הוא הידוע ביותר וכנראה גם העתיק ביותר מבין חידות הבור. זוהי למעשה משפחה של חידות, אשר המשותף להן הוא צורתם הבסיסית של החלקים וצורתה של החידה כשהיא מורכבת.
במשך שנים רבות, סוג זה של חידות היה נפוץ ועממי אך נחשב לנדוש ולא מעניין. החידות שנוצרו ונמכרו היו דומות מאד אחת לשנייה ויחסית קלות לפירוק, כי ברובן אחד החלקים היה מוט שלם ללא חריצים אשר מחליק בקלות החוצה. בסוף שנות השבעים, חזר ה"בור 6 חלקים" לעורר עניין בקרב העוסקים בתחום, בעיקר הודות לאנליזה ממוחשבת שביצע המתמטיקאי ביל קטלר ופרסומה בטור של מרטין גרדנר בכתב העת סיינטיפיק אמריקן.[6]
מבנה
ששת החלקים של החידה הם מוטות ריבועיים באורך זהה (שהוא לפחות פי 3 מרוחבם), אשר במצב מורכב מסודרים בשלושה זוגות המצטלבים זה בזה. החריצים של כל מוט נמצאים באזור ההצטלבות שבין המוטות, כך שאינם נראים כאשר החידה מורכבת. ניתן לתאר את החריצים כהסרה של יחידות בצורת קובייה (שמידתן חצי מרוחב המוט) כפי שמתואר באיור:
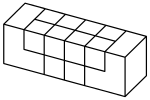
ישנן 12 יחידות קובייה הניתנות להסרה. חידות שונות מסוג זה מורכבות ממוטות שהוסרו מהם יחידות שונות. קיימות 4,096 אפשרויות שונות להסרת יחידות קובייה מהמוט. מתוך אלו מתעלמים מאפשרויות החותכות את המוט לשניים או שיוצרות חלקים זהים, ומקבלים 837 חלקים שונים[7]. חלקים אלו יכולים תאורטית להשתלב לחידת בור בכ-35 מיליארד דרכים, אך ההערכה היא כי פחות מ-6 מיליארד מהן ניתנות לפירוק והרכבה.[8]

בור מלא
חידות בור שאין להן חללים פנימיים כשהן מורכבות מכונות בור מלא (Solid Burr). בחידות אלה יוצא החלק הראשון, או כמה חלקים יחד, בתזוזה אחת. עד לשנות השמונים, קיבלו חידות הבור המלא את מירב תשומת הלב וכל הפרסומים המקצועיים עד אז התייחסו לסוג זה בלבד.[10] ניתן להרכיב 119,979 חידות כאלה, עם 369 סוגי חלקים. להרכבת כל החידות יידרש סט של 485 חלקים, מפני שבחלק מהחידות נעשה שימוש בחלקים זהים.[7]

סוגי החלקים
מטעמים אסתטיים, אך בעיקר מטעמים מעשיים, נהוג להתייחס לחלקים משני סוגים:
- חלקים חריציים (Notchable) אשר להם חריצים שלמים וניתן לייצר אותם באמצעות מסור או כרסומת.
- חלקים לא-חריציים (Non-notchable) אשר להם פינות פנימיות הניתנים לייצור רק באמצעות חריתה באזמל או על ידי הדבקה.

קיימים 59 חלקים חריציים, כולל המוט השלם ללא חריצים. מתוכם 25 חלקים יכולים לשמש להרכבת חידות בור מלא. מחלקים אלו, המכונים לעיתים "סט 25 החריציים", בתוספת 7 חלקים כפולים, ניתן להרכיב 314 חידות שונות. חלקים אלו הם פופולריים מאד וחברות רבות מייצרות ומוכרות סטים שלמים שלהם.
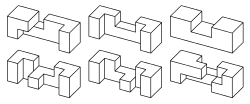
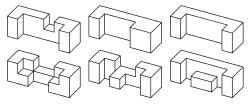
בור חלול
בכל חידות הבור המלא נדרשת תזוזה אחת בלבד כדי להוציא את החלק הראשון. לעומת זאת, בין החידות מסוג בור חלול (Holey Burr), שיש להן חללים פנימיים כשהן מורכבות, ישנן גם כאלה הדורשות לשם כך מספר תזוזות של חלקים. מספר התזוזות הנדרשות להוצאת החלק הראשון נקרא הדרגה של הבור, כלומר כל חידות הבור המלא הם מדרגה 1. ככל שדרגת הבור גבוהה יותר, הוא קשה יותר לפתרון.
בשנות השבעים והשמונים ניסו מומחים למצוא חידות בעלות דרגה כמה שיותר גבוהה. בשנת 1979 מצא סטיוארט קופין האמריקאי בור בדרגה 3. בשנת 1985 מצא ביל קטלר בור בדרגה 5[11] ומעט אחר כך מצא פיליפ דובואיז הישראלי בור בדרגה 7.[10] בשנת 1990 השלים קטלר את החלק האחרון של מחקרו ומצא כי הדרגה הגבוהה ביותר של בור עם פתרון יחיד המורכב מחלקים חריציים היא 5, וקיימים 139 כאלה. הדרגה הגבוהה ביותר האפשרית עם יותר מפתרון אחד היא 12, כלומר נדרשות 12 הזזות לפני הוצאת החלק הראשון.[8]
בור 3 חלקים

בור 3 חלקים הבנוי מחלקים "רגילים" (בדומה לבור 6 חלקים) אינו ניתן לפירוק והרכבה.[12] למרות זאת, קיימות חידות בור 3 חלקים המורכבות מחלקים בצורות שונות. המוכר בהן מתואר בספרו של אדווין וויאט משנת 1928, שאחד מחלקיו מעוגל וניתן לסיבוב.[1]
משפחות מוכרות של חידות בור

אלטקרוז
האלטקרוז (Altekruse) נקרא על שמו של ויליאם אלטקרוז אשר קיבל עליו פטנט בשנת 1890, למרות שמקור החידה הוא כנראה קדום יותר.[13] מקור השם אלטקרוז הוא אוסטרי-גרמני ומשמעותו "צלב ישן", מה שגרם לרבים לחשוב כי מדובר בשם עט, אך אדם בשם זה היגר לארצות הברית ב-1844 עם שלושת אחיו כדי להימנע מגיוס לצבא הפרוסי והוא כנראה בעל הפטנט.[14]
האלטקרוז הקלאסי בנוי מ-12 חלקים זהים ופירוקו דורש תזוזה של שני חצאי החידה לכיוונים מנוגדים. עם שני חלקים זהים נוספים ניתן להרכיב את החידה בצורה נוספת. על פי עקרון דומה, ניתן ליצור חידות נוספות ממשפחת האלטקרוז, עם 6, 24, 36 חלקים, וכן הלאה. למרות גודלן, חידות אלו אינן קשות מאד להרכבה אך דורשות סבלנות ומיומנות מוטורית.

צ'אק
הצ'אק הומצא על ידי אדוארד נלסון אשר קיבל עליו פטנט בשנת 1879.[15] דגם זה שוכלל ושופר על ידי רון קוק מחברת Pentangle הבריטית[16] אשר הוסיף דגמים נוספים.
הצ'אק בנוי בעיקר ממוטות באורכים שונים החתוכים לצורת האות "כ" ומעט חלקים בעלי חריץ נוסף הנקראים "חלקי מפתח". כדי ליצור חידות צ'אק גדולות יותר (אשר מכונות על יד קוק "אבא-צ'אק", "סבא-צ'אק" ו"סבא-רבא-צ'אק") יש צורך להוסיף חלקים ארוכים יותר. ניתן להסתכל על הצ'אק גם כהרחבה של חידת "בור 6 חלקים" קלאסית, בעלת חלקים פשוטים. חידה כזו מכונה "תינוק-צ'אק" והיא קלה מאד לפתרון. עם חלקים של חידות צ'אק באורכים שונים ניתן גם להרכיב צורות שונות שאינן סימטריות, על פי עקרון ההרכבה של החידה המקורית.


פאגודה
מקורה של הפאגודה, המכונה גם "קריסטל יפני", אינו ידוע. החידה מוזכרת בספרו של וויאט משנת 1928.[1] החידות בסדרת הפאגודה הן למעשה הרחבה של חידת "בור 3 חלקים" (פאגודה בגודל 1), אך הן ניתנות לפירוק והרכבה ללא סיבוב של אחד החלקים. פאגודה בגודל 2 מורכבת מ-9 חלקים והגדולות יותר מ-19, 33, 51 וכן הלאה. פאגודה בגודל מורכבת מ- חלקים.
בור אלכסוני

למרות שרובן של חידות הבור מורכבות ממוטות בעלי חריצים ריבועיים, קיימות גם חידות שהחריצים בהן אלכסוניים. בבור אלכסוני, המוטות ריבעיים והחריצים הם בצורת V ובזווית של 45° מפאות המוט. חידות אלו מכונות לעיתים "כוכב" מפני שנהוג לחתוך, לשם האסתטיקה, את הקצוות של המוטות גם כן בזווית של 45°, מה שנותן לחידה המורכבת מראה המזכיר כוכב או מגן דוד.
ראו גם
לקריאה נוספת
- Coffin, Stewart T., 2007, Geometric Puzzle Design, Wellsley, K. Peters מסת"ב 1568813120
- Wyatt, Edwin Mather, 1981, Puzzles in Wood. Milwaukee, Wisc: Bruce Publishing Co. מסת"ב 0918036097
קישורים חיצוניים
- ספרו של סטיוארט קופין, The Puzzling World of Polyhedral Dissections בגרסת אינטרנט (זו המהדורה הקודמת של ספרו Geometric Puzzle Design) (באנגלית)
- אתר החידות של ישינו קייצ'ירו המכיל תיאור ופתרונות של מאות חידות בור. (באנגלית)(ביפנית)
- פרק על חידות בור בדף החידות של רוב (באנגלית)
- אתר חידות הבור של IBM שנוצר ב-1997 על ידי ג'ורג ון-קנל (Jürg von Känel) ובו תוכנת ג'אווה לפתרון חידות בור, בארכיון האינטרנט. (באנגלית)
- מבחר חידות בור באתר של "גאיה משחקי חשיבה"
- מבחר משחקי חשיבה לילדים גם מעץ באתר של "בית הצעצוע".
הערות שוליים
- ^ 1.0 1.1 1.2 Wyatt, Edwin Mather, Puzzles in Wood, Milwaukee, The Bbuce Publishing Company, 1928. (New Edition: מסת"ב 1565233484)
- ↑ Slocum, Jerry, New Findings on the History of the Six Piece Burr, Slocum Puzzle Foundation.
- ↑ Slocum, Jerry and Dieter Gebbardt, Puzzles from Catel's Cabinet and Bestelmeier's Magazine, 1785 to 1823, Slocum Puzzle Foundation, 1997.
- ↑ Wei Zhang and Peter Rasmussen, Chinese Puzzles: Games for the Hands and Mind, Art Media Resources, 2008. מסת"ב 1588861015 (פרק על בור באתר הספר)
- ↑ פטנט מספר 1225760 של אוסקר בראון, באתר משרד הפטנטים האמריקאי
- ↑ Gardner, Martin. "Mathematical Games", Scientific American. January 1978, pp. 14-26
- ^ 7.0 7.1 Cutler, William H. "The Six-Piece Burr", Journal of Recreational Mathematics. Vol 10(4), 1977-78, pp. 241-250
- ^ 8.0 8.1 אנליזה ממוחשבת של כל חידות בור ב-6 חלקים משנת 1994 באתר של ביל קטלר
- ↑ Hoffmann, Professor, "Puzzles old and new", London, Frederick Warne and Co., 1893, Chapter III, No. XXXVI. (זמין להורדה בארכיון האינטרנט)
- ^ 10.0 10.1 Coffin, Stewart. Puzzle Craft, 1992, p.34
- ↑ Dewdney, A. K. "Computer Recreations", Scientific American, Vol 253, Issue 4, Oct. 1985, pp. 16-27
- ↑ בור 3 חלקים באתר חידות הבור של IBM
- ↑ פטנט מספר 430502 של ויליאם אלטקרוז, באתר משרד הפטנטים האמריקאי
- ↑ The Altekruse Puzzle from Coffin, Stewart T., The Puzzling World of Polyhedral Dissections
- ↑ פטנט מספר 588705 של אדוארד נלסון, באתר משרד הפטנטים האמריקאי
- ↑ דף חידות צ'אק באתר של Pentangle
שגיאות פרמטריות בתבנית:מיון ויקיפדיה
שימוש בפרמטרים מיושנים [ דרגה ] חידת בור22375459


