שבירה

שבירה היא תופעה פיזיקלית שבה גל עובר מתווך אחד אל תווך שני. במקרה הכללי חלק ממשרעת הגל מוחזר ממשטח הגבול המפריד בין שני התווכים, ושאר המשרעת עובר לתווך השני.
בתווך השני במקרה הכללי משתנה כוון התקדמות הגל וגם אופי הגל. בדרך כלל תדירות הגל נשמרת, אך אורך הגל משתנה. גל אלקטרומגנטי שאינו מקוטב יכול להפוך למקוטב במעבר, וגל אקוסטי יכול להפוך מאורכי לרוחבי. מעבר תווך יכול לפזר בזוויות שונות תדרים שונים בגל המועבר; עובדה זו מהווה את הבסיס לתופעת הנפיצה. ההסברים הקלאסיים לתופעות כמו שבירה והחזרה, מבוסס על עקרונות שנתגלו באופן ניסויי, דוגמת עקרון הויגנס, או על תובנות עיוניות בעלות אופי כולל (מאקרוסקופי), כמו עקרון פרמה. התמונה היסודית יותר, המיקרוסקופית, מבוססת על אינטראקציה בין הגל הפוגע לבין החומרים מהם עשויים התווכים השונים.
תופעת השבירה היא כללית וחלה על כל סוגי הגלים. עם זאת מאמר זה עוסק בגלים אלקטרומגנטיים כמודל, ובפרט, בגלי אור.
המשמעות הפיזיקלית של פיצול הגל במעבר בין תווכים היא שחלק מהאנרגיה הנישאת בגל מתקדם הלאה, וחלק שלה מוחזר לאחור. למשמעות זו חשיבות מרובה הן באופטיקה והן בתקשורת אלקטרונית של מערכות שידור ומוליכי גלים, מאחר שחלק מהאנרגיה המשוגרת איננו יעיל, מתבזבז ואף עלול לגרום לנזק. למשל, רכיביהן של מערכות אלקטרוניות מחוברים זה לזה דרך כבלים, באמצעות מתאמים היוצרים תיאום עכבות ביניהם. תיאום זה דרוש למניעת הספק חוזר של האות החשמלי[1] המתקדם מרכיב אחד לרכיב אחר.
קרניים וחזיתות גלים


נהוג לתאר את התפשטותם של גלים באמצעות חזיתות גלים או בעזרת קרני-אור. שתי ההצגות קשורות ביניהן, כפי שמיד נראה. חזית גל היא המקום הגאומטרי של כל הנקודות במרחב בו מתפשט הגל, הנמצאות באותו מופע.
דוגמאות:
- חזית גל מישורית - חזית גל המגיעה ממקור מרוחק היא בקירוב, מישורית.
- חזית גל מעגלית - חזית כזו מתקבלת ממקור נקודתי[2]. איור 2 מימין, מראה גל מישורי הנשבר אל תווך חדש, בכיוון חדש. כיוון ההתפשטות החדש נקבע כאן באמצעות עקרון הויגנס.
האיור הבא (איור 3, מונפש) לעומת זאת, ממחיש את האופן בו נשברת חזית גל מעגלית - היא הופכת לאליפטית בדיוק מאותם שיקולים המסבירים את סטייתה מכיוונה המקורי, של החזית המישורית באיור הקודם.
בכל נקודה ונקודה על חזית הגל המתפשט, האנך לחזית הגל מתווה את כיוון התפשטות הגל באותה נקודה, והוא מיוצג באופן גרפי, על ידי קרן. במקרה של חזית גל מישורית, כל הנקודות מתקדמות באותה מהירות ובאותו כיוון, ולכן הקרניים תהיינה מקבילות. במקרה של חזית גל מעגלית, מהירותם תהיה אמנם אחידה, אבל בכיוונים שונים, כלומר, הקרניים תהיינה רדיאליות. שתי דוגמאות אלה הן דוגמאות קצה בלבד, אם כי שימושיות מאוד.
חוקי השבירה
נתבונן שוב באיור 1. באיור זה מתוארות קרן הפוגעת בזווית ϕ1, וקרן הנשברת בזווית ϕ3.
- הקרן הפוגעת, הקרן הנשברת, הקרן המוחזרת והאנך למשטח בנקודת הפגיעה, נמצאות כולן באותו מישור[3], הקרוי מישור הפגיעה.
- זווית הקרן הפוגעת ביחס לאנך שווה לזווית הקרן המוחזרת.
חוק סנל
הקשר בין זווית הפגיעה לבין זווית השבירה ניתן על ידי , כאשר n1 ו-n2 הם מקדמי השבירה של התווכים המתאימים. קשר זה קרוי, על שם מגלהו, חוק סנל.
מקדם שבירה גבוה, מבטא את כושרו של התווך לעכב בצורה יעילה יותר את האור העובר דרכו, כלומר מהירות התפשטות האור בתווך זה קטנה יותר. מקדם שבירה מוגדר לפיכך, על ידי , כאשר, c היא מהירות האור בריק, ו-v היא מהירות התפשטותו בתווך.
מהביטוי לחוק סנל, רואים כי במעבר האור מתווך בעל מקדם שבירה אחד לתווך בעל מקדם שבירה גדול יותר, לדוגמה, במעבר מאוויר לזכוכית, זווית השבירה אז, קטנה יותר מזווית הפגיעה. משמעות הדבר היא שהקרן מוסטת פחות ביחס לאנך, לאחר שבירתה. תוצאה הפוכה מתקבלת במעבר הפוך, כלומר אל תווך בעל מקדם שבירה קטן יותר. הערה: מביטוי זה גם רואים שלא מתרחשת שבירה כאשר האור פוגע בניצב למשטח הפגיעה, שכן אז האור פוגע בזווית של 0, ולכן גם זווית השבירה היא 0.
החזרה פנימית גמורה

 ערך מורחב – החזרה פנימית מלאה
ערך מורחב – החזרה פנימית מלאה
בתנאים מסוימים, כל האור הפוגע מוחזר לתווך המקורי, מבלי שתתרחש שבירה כלל. תנאים אלה מתקיימים במצב בו האור עובר לתווך בעל מקדם שבירה קטן יותר. בשל העובדה שזווית השבירה תמיד מקדימה את זווית הפגיעה (ראו איור 4, קרן ירוקה), כלומר היא תמיד גדולה ממנה, היא מגיעה ראשונה, לערך של 900. במילים אחרות, ישנה זווית פגיעה שעבורה זווית השבירה היא כבר 900. במצב זה אין קרן היוצאת אל התווך השני, כיון שהיא נותרת 'כלואה' במשטח המפריד בין שני התווכים (הקרן הצהובה באיור ממחישה זאת). זווית זו מוגדרת כזווית הגבול או זווית פגיעה קריטית. עבור זוויות פגיעה הגדולות ממנה, תתרחש כבר החזרה מלאה פנימה, בהתאם לחוקי ההחזרה (ראו קרן אדומה באיור), והקרניים נותרות לכודות בתוך התווך. תופעה זו מכונה החזרה פנימית גמורה, ולה יישומים רבים, בעיקר בתחומי הדמיה לצורכי איבחון וטיפול רפואיים ותקשורת אופטית, בהם נעשה שימוש רב בסיבים אופטיים המנצלים את התופעה. לסיבים כאלה יתרונות טכנולוגיים גדולים מאוד, משום שבתכנון נכון של המערכת, הסיבים מאפשרים הפסדים מינימליים בקווי התקשורת, גם מבחינת נצילות אנרגטית[4], אבל גם מבחינת יחס אות לרעש, המתבטא ביעילות העברת מידע טובה בהרבה.
ההוכחה היסודית ביותר לנכונותם של חוקים אלה, מתבססת על משוואות מקסוול, מאחר שאלה מטפלות בקשר בין רכיביו החשמלי והמגנטי של גל אלקטרומגנטי (דוגמת אור), ובינם לבין כיוון התקדמותו[5]. עם זאת, ניתן להוכיח את חוק סנל בעזרת עקרונות אחרים, פשוטים יותר, כמו עקרון הויגנס. הסעיף הבא, מוקדש להוכחתו של חוק סנל, בהסתמך על עקרון פרמה.
קבלת הביטוי לחוק סנל
ניעזר לשם כך בעקרון פרמה[6]. על פי נוסחו המודרני [כלומר, כזה שבו נלקחים בחשבון לא רק המסלול, אלא גם הבדלים במקדם השבירה לאורך המסלול, או במילים אחרות, בהתחשב באי אחידות אופטית, לאורך המסלול] יותר של עיקרון זה: מסלולה של קרן אור מנקודה אחת לנקודה שנייה, דרך כל מערך של תווכים, הוא כזה, שהדרך האופטית אותה היא עוברת, נותרת ללא שינוי בקירוב ראשון, גם תחת וריאציות של דרך זו. במילים אחרות, הדרך האופטית המינימלית, נוהגת כמו ערך קיצון של פונקציה, שבמקרה זה היא מסלולה של הקרן. בהסתמך על הבנה זו, נבדוק מתי מסלול הקרן מקבל ערך קיצון, ובמקרה שלנו, ערך מינימלי.

נתבונן באיור 5, להלן.
באיור זה, מתוארת קרן אור היוצאת מנקודה A בתווך שמקדם השבירה שלו n1, ומגיעה לנקודה B הנמצאת בתווך n2, לאחר שהיא נשברת בנקודה P, על משטח גבול מישורי המפריד ביניהם, כפי שמוראה באיור. אורכה של הדרך האופטית מ-A ל-B הוא , ולאחר הצבת ו- בביטוי זה, בהסתמך על משפט פיתגורס, נקבל , כאשר כל הגדלים הגאומטריים מוגדרים באיור הנתון.
עתה, כדי לקבל x המתאים לדרך אופטית מינימלית, בהתאם לעקרון פרמה, נגזור את הביטוי שקיבלנו לפיו, לפי המשתנה x, ונשווה אותו ל-0, על מנת לקבל את ערך הקיצון של הדרך האופטית, (נקודת מינימום או מקסימום) [יש כאן חזרה בעניין הקיצון - לשנות זאת]. משתנה הגזירה נבחר כ-x, מאחר שהוא קשור בשיפועי הקרן הפוגעת והקרן הנשברת, כפי שמוראה בהמשך [להכניס להערת שוליים]. מפעולות אלה נקבל , ומהאיור ברור מיד כי ביטוי זה שקול לביטוי , המוכר.
הקשר בין תופעת השבירה לבין תופעת הנפיצה

מקדם שבירה אינו מאפיין רק את החומר, אלא גם את אורך הגל - בחומר יחיד ייתכנו מקדמי שבירה שונים לגלים עם אורך גל שונה (או תדירות שונה) - תופעה המכונה נפיצה. שבירת אור היא הדרך הנפוצה ביותר להמחיש נפיצה, וכך למעשה התגלתה התופעה במקור על ידי אייזק ניוטון[7] - כאשר אור אשר מורכב מצבעים שונים (למשל אור שמש, או כל אור לבן) פוגע בחומר אשר מקדם השבירה שלו שונה כתלות בצבע, כל צבע נשבר בזווית אחרת בהתאם למקדם השבירה שלו. במקרה של אור לבן נוצרת כך קשת שמורכבת מכל הספקטרום - כך הראה ניוטון ש״לבן״ הוא לא צבע בודד אלא אור שמורכב מכלל הצבעים גם יחד. מנסרה היא הרכיב הפשוט ביותר להצגת נפיצה כזו, ובו השתמש בין היתר גם ניוטון. תמונת האור הנשבר במנסרה ומתפצל לאורכי הגל השונים בעקבות נפיצה הפכה לאייקונית והופיעה בין היתר על כריכת האלבום The Dark Side of the Moon של להקת פינק פלויד.
תופעה נוספת שמערבת שילוב של שבירה ונפיצה היא קשת בענן; במקרה זה, הנפיצה היא בשבירה מטיפות מים קטנות.
שבירה בעדשות

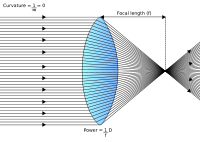
תופעת השבירה מנוצלת באופן המגוון והנרחב ביותר בתחום של תכנון עדשות ושימוש בהן, לצרכים ויישומים רבים, יומיומיים, תעשייתיים ומדעיים.
המבנה של עדשה מורכב מחתך כדורי, על פי רוב, אחד, או שניים. מבנה זה מקנה להן את תכונתן העיקרית, והיא כושרן למקד, בקירוב, קרניים מקבילות לנקודה אחת. יכולתן זו למקד אלומות מקבילות מתבטאת ביצירת מיפוי ממוקד של אלומות כאלה, המגיעות מאזורים שונים[8], וליצור על ידי כך דימות של עצמים. דוגמאות: משקפיים, צילום ועוד.
שימוש בעדשות מאפשר קבלת תכונות אופטיות נוספות, כמו הגדלה של הדמות המתקבלת. תכונה זו מנוצלת בשני תחומים עיקריים: טלסקופיה, בה מערכת של עדשות משמשת להגדלת דמויותיהם של עצמים רחוקים מאוד (כוכבים, למשל) ומיקרוסקופיה, בה מערכת של עדשות משמשת להגדלת דמויותיהם של עצמים קטנים מאוד, לשם בחינת תאים וגופים זעירים אחרים.
עם זאת, עדשות סובלות מסדרה של חסרונות, והעיקריים שבהם הן אברציות אופטיות, כמו האברציה הכרומטית, שמקורה במוקד שונה עבור אורכי גל שונים, כתוצאה מנפיצה. כדי לפתור בעיות מסוג זה, מערכות אופטיות איכותיות (מצלמות ואמצעי צפייה למיניהם) המיועדות לקבלת דמות איכותית של העצם, עושות שימוש בצירופי עדשות, המתוכננים כך, שהן מתקנות זו את סטיותיה של זו.
תופעות קשורות


אשליה של עצם שבור, השקוע בנוזל
התמונה מימין ממחישה את תופעה השבירה באופן בלתי אמצעי. ההסבר לכך קשור במהלך האור. אור מגיע אל הקשית בצורה מפוזרת ממקורות שונים בסביבת הכוס, ומוחזר ממנה לכל העברים, כולל אל עינו של הצופה (או הצלם במקרה זה). בדרכן של קרני האור מהנוזל, החוצה לאוויר, הן נשברות, ומוסחות עתה רחוק יותר מהאנך, כמו בכל מקרה של מעבר ממקדם שבירה גבוה למקדם שבירה נמוך יותר. קרן כזו נתפסת במרכז הראיה במוח כאילו היא מתפשטת בקו ישר בלבד, מה שיוצר את האשליה של המשך הקרן לאחור, כלומר חלקה השקוע של הקשית נראה מוגבה יותר, וכאילו היא שבורה.
עומק מדומה

האיור משמאל מתאר עצם הנראה לצופה בעומק שונה ממצבו האמיתי. הסברה של תופעה זו דומה מאוד לזה של התופעה הקודמת, ולמעשה זהה, מלבד מוקד ההתעניינות. בדוגמה הקודמת, התייחסנו לגוף שרק חלקו שקוע, ומטבע הדברים, הצופה נוטה להשוות את חלקה הפנימי של הקשית, לחיצוני. בדוגמה המובאת כאן, הגוף טבול כולו בנוזל, ולכן בולט ההיבט של עומק מדומה.
על אף שהסברה המדעי של התופעה החל להתברר רק במאה ה-17, בכל זאת, ידוע על מסורות דייג קדומות (למשל, אצל שבטי אינדיאנים מסוימים באמריקה), שנהגו לקחת בחשבון את עומקם המדומה של דגים אותם בקשו לצוד.
יתר על כן, ישנן למשל, ציפורים הצוללות אל תוך המים בכיוונו האמיתי של הדג, ולא בכיוונו הנראה[9].
כאשר מתבוננים בנוזל מלמעלה מתווך אחד לתווך שני, ניתן להראות היחס בין הגובה האמיתי H לגובה המדומה h שווה בקירוב ליחס בין מקדמי השבירה של שני התווכים ביחס לריק.
כאשר נמצאים מתחת למים ומסתכלים מעלה אל כיוון האוויר, רואים רק את האזור מעל המים שנמצא בתוך חרוט אור בזווית 97 מעלות, מכיוון שמעבר ל-48.5 מעלות מתרחשת החזרה מלאה והאור אינו עובר.
שקיעת השמש
צפיפות המולקולות באטמוספירה איננה קבועה, והיא עולה, בצורה הדרגתית, ככל שמתקרבים לפני הקרקע. עובדה זו גורמת לכך שקרן אור החולפת דרך האטמוספירה, אינה עושה את דרכה בקו ישר, אלא במסלול עקום. משמעות הדבר היא שמקומה של השמש בשקיעה, הוא גבוה יותר ממצבה האמיתי, בשל אותה סיבה שתוארה בדוגמה של עומק מדומה.
תופעת הקשת
תופעה זו נצפית, בתנאים מסוימים, כאשר האוויר בסביבתו של הצופה נעשה רווי ברסיסי מים, לדוגמה, אחרי גשם, או בקרבת ממטרות או מפלי מים. בתופעה זו מעורבים כמה תהליכים אופטיים, וביניהם שבירה, נפיצה והחזרה. קרני האור נשברות במעברן לתוך רסיסי המים ומוחזרות בזוויות מסוימות מהדופן הפנימית שלהם. מאחר שהשבירה אל תוך רסיס המים איננה אחידה, כלומר, עקב נפיצה אורכי גל שונים נשברים בזוויות שונות, ולכן גם מוחזרים בזוויות שונות, ומכאן צבעי הקשת.
ראו גם
לקריאה נוספת
- פרופ' יורם קירש ומיכל בן-יעקב, יסודות הפיזיקה ב', האוניברסיטה הפתוחה, 1998 (הספר במיזם פא"ר) (יחידה 3, פרק 2)
- מבוא לאופטיקה קלאסית ומודרנית, כרך א', האוניברסיטה הפתוחה, 1995, פרקים 1.2 ו-1.3.
- Physics, D Halliday & R Resnick, Wiley (3rd edition), 1977, chap.43&44.
- Optics, E. Hecht, Addison-Wesley (2nd edition), 1987, chap.4.
- Fundamentals of Optics, FA Jenkins & HE White, McGraw-Hill (4th edition), 1976, chap.1&2.
קישורים חיצוניים
- הדגמה אינטראקטיבית של חוק סנל
- שבירה, באתר אנציקלופדיה בריטניקה (באנגלית)
 שבירה, דף שער בספרייה הלאומית
שבירה, דף שער בספרייה הלאומית
הערות שוליים
- ↑ בתחומי אלקטרואופטיקה ותקשורת אלקטרונית, נהוג להשתמש במונח אות (חשמלי או אלקטרוני, או אף אופטי) במקום גל
- ↑ כלומר שממדיו קטנים, יחסית.
- ↑ עובדה זו נכונה במקרה של שבירה 'רגילה', בניגוד לשבירה 'לא רגילה', כמו במקרה של הקרן השנייה בשבירה כפולה.
- ↑ בוודאי בהשוואה לקווי תמסורת מתכתיים רגילים, המשמשים להולכת אותות חשמליים
- ↑ למרות שאלה נוסחו מאוחר יותר
- ↑ מעיקרון זה, ניתן לקבל לא רק את חוק סנל, אלא גם את חוקי ההחזרה.
- ↑ Beautiful Experiments: Newton’s Decomposition of Sunlight
- ↑ אזורים אלה נבחרים כך שגודלם מספיק קטן כדי שהקרניים המגיעות מהם ייחשבו מקבילות על פני העצם
- ↑ התנהגות זו שונה מהתנהגות אחרת, המהווה צורה אחרת של התמודדות, בה העוף צולל בניצב למים, ובכך מנטרל את הסטיה.
| גלים | ||
|---|---|---|
| מאפיינים | משרעת • תדירות • מופע • אורך גל • וקטור גל • מספר גל • מהירות פאזה • מהירות חבורה • קיטוב | 
|
| תופעות | החזרה • העברה • שבירה • התאבכות • עקיפה • נפיצה • בליעה | |
| מושגים | גל עומד • אפנון • חבילת גלים • תווך • מתנד הרמוני • תהודה • אפקט דופלר | |
| אנליזה | משוואת הגלים • משוואת הלמהולץ • עקרון הויגנס • עקרון פרמה • חוקי פרנל | |
| סוגי גלים | גל מישורי • גל כדורי • גל רוחב • גל אורך • פולס • קרינה אלקטרומגנטית • גל קול • גל (מים) • פונקציית גל | |
שבירה41592601Q72277


