שדה וקטורי סולנואידי
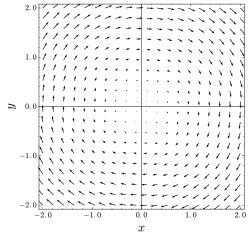
באנליזה וקטורית, שדה וקטורי סולנואידי (לעיתים נקרא גם שדה וקטורי אי-דחיס, בהקשר למכניקת הזורמים) הוא שדה וקטורי v עם דיברגנץ אפס בכל הנקודות במרחב:
באופן אינטואיטיבי ניתן לומר שקווי השדה של שדה סולנואידי אינם "מתכנסים" לאף נקודה, כלומר שאין להם מקורות או בולענים (sink).
תכונות
המשפט היסודי של האנליזה הווקטורית קובע שכל שדה וקטורי ניתן לבטא כסכום של שדה אי-רוטציוני ושדה סולנואידי. התנאי של דיברגנץ אפס מתקיים רק כאשר לפוטנציאל המתאים לשדה וקטורי v יש מרכיב של פוטנציאל וקטורי בלבד, זאת כיוון שמההגדרה של הפוטנציאל הווקטורי A:
נובעת אוטומטית הזהות הווקטורית:
הטענה ההפוכה גם תקפה: בעבור כל שדה סולנואידי v קיים פוטנציאל וקטורי A כך ש- (ראו גם פירוק הלמהולץ (אנ')).
משפט הדיברגנץ מספק הגדרה אינטגרלית שקולה לשדה סולנואידי; לכל משטח סגור, השטף הכולל של שדה וקטורי סולנואידי v דרך המשטח חייב להיות אפס:
כאשר dS הוא הווקטור הנורמל לאלמנט שטח.
דוגמאות
- השדה המגנטי B (ראו גם משוואות מקסוול),
- שדה המהירות של זורם אי-דחיס,
- שדה הערבוליות,
- שדה חשמלי באזורים נייטרליים (); זוהי דוגמה מנוונת כאשר עוסקים בשדות מגנטיים לא משתנים בזמן,
- הפוטנציאל הווקטורי המגנטי A בכיול קולון.
ראו גם
קישורים חיצוניים
- שדה וקטורי סולנואידי, באתר MathWorld (באנגלית)
שדה וקטורי סולנואידי31693324Q1265039


