ערימה בינומית
| ערימה בינומית | |||
|---|---|---|---|
 ערימה בינומית עם 13 איברים | |||
| סיבוכיות מקום וזמן | |||
| |||
| זיכרון: |
| ||
| חיפוש: |
| ||
| הכנסה: |
| ||
| הוצאה: |
| ||
| שליפה: |
| ||
| הצצה: |
| ||
במדעי המחשב, ערימה בינומית היא סוג של מבנה הנתונים ערימה. היא ממומשת בעזרת אוסף עצים בינומים. יתרונה הוא שהיא מאפשרת מיזוג שתי ערימות במהירות.
ערימה בינומית מהווה מימוש יעיל של מבנה הנתונים המופשט תור עדיפויות.
מבנה
ערימה בינומית ממומשת כאוסף של עצים בינומיים. כל עץ בינומי מקיים את "כלל הערימה": ערך כל צומת קטן יותר מערכי כל בניו (ערימה כזאת נקראת "ערימת מינימום". ניתן גם לבנות "ערימת מקסימום", בה כל צומת גדול מבניו).
תכונת הערימה הבינומית
ערימה בינומית מקיימת את השמורה הבאה: לכל i, יש בערימה לכל היותר עץ אחד מדרגה i.
דרגה של עץ בינומי מוגדרת על ידי מס' הצמתים בעץ, כך שעץ מדרגה 0 הוא שורש בלבד, ובעץ מדרגה i יש קודקודים.
כתוצאה מכך יש מבנה אפשרי יחיד לערימה, הנובע מהייצוג הבינארי של גודלה. (לדוגמה, בערימה מגודל 25 (11001 בבסיס בינארי) יהיה עץ אחד מדרגה 0, עץ אחד מדרגה 3 ועץ אחד מדרגה 4). את שורשי העצים ניתן להחזיק ברשימה מקושרת כפולה (כלומר עם מצביעים אחורה).
מאפיינים
בערימה בינומית יש לכל היותר עץ אחד מכל דרגה. לפיכך, בערימה בינומית בה דרגת העץ המקסימלי היא i יש לכל היותר 2^(i+1) איברים. לפיכך, בערימה בינומית בה יש m איברים- יש לכל היותר עצים.
פעולות
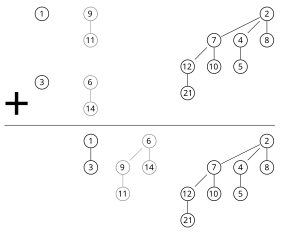
הפעולה המעניינת והחשובה ביותר בערימה בינומית היא מיזוג:
מיזוג
בהינתן שתי ערימות, ממזגים אותן בדומה לחיבור בינארי: עוברים על הדרגות מהקטנה לגדולה, ובכל דרגה, אם יש רק עץ אחד מדרגה כזו מכניסים לערימה המאוחדת. אם יש שניים, מאחדים אותם ומתייחסים אליהם כאל עץ מדרגה גדולה יותר (בדומה לנשא בחיבור רגיל). כיוון שישנם כ-log m עצים בכל ערימה, הסיבוכיות היא .
כעת נבחן כיצד לממש את שאר פעולות הערימה באמצעות פעולות המיזוג:
הכנסה
כדי להכניס אלמנט חדש, נבנה ערימה חדשה מדרגה 1 ונמזג אותה עם הערימה הקיימת.
סיבוכיות הפעולה היא (כש-m הוא גודל הערימה), אך ניתוח לשיעורין מביא לתוצאה של . (ומכאן שבניית ערימה מ-m איברים לוקחת )
מחיקת המינימום
הואיל וכל אחד משורשי העצים בערימה מקיים את תכונת הערימה, הרי שאיבר המינימום בערימה הוא אחד משורשי העצים. הואיל ובערימה בת m איברים יש log m שורשי עצים, ניתן למצוא את שורש המינימום ב- O(log m). מוצאים את איבר המינימום ומוחקים אותו. (ניתן, כשיפור, להחזיק מצביע לאיבר המינימלי, כך שמציאתו לוקחת .)
כיוון שילדיו של עץ מדרגה i הם שורשים של עצים מדרגות i-1,...,0,1, ניתן להסתכל על שורשיו כערימה בינומית מסדר i-1. כעת מבצעים מיזוג בין הערימה החדשה הזו לשאר הערימה. סיבוכיות: .
מחיקה
כיוון שערימה אינה תומכת בחיפוש, מחיקה צריכה לבוא עם מצביע לאיבר הנמחק. כדי למחוק מחליפים את ערך הצומת עם אביו, ואז שוב עד לשורש (פעולה זאת לוקחת כעומק המקסימלי של עץ שהוא כ-log m), ואז מוחקים אותו וממזגים את בניו עם שאר הערימה. סיבוכיות: .
הקטנת מפתח
בהינתן מצביע לצומת מסוים, מקטינים את המפתח, ואם הוא קטן מאביו, מחליפים ביניהם, ושוב אם הוא קטן מאביו מחליפים ביניהם עד שהוא גדול מאביו (או מגיע לשורש), סיבוכיות: . שיפור בסיבוכיות של פעולה זו אפשרי על ידי שימוש בערימת פיבונאצ'י, המבוססת על ערמה בינומית, בה עלות הקטנת מפתח בניתוח לשיעורין היא .
וריאציות
ערימה בינומית עצלה
ערימה בינומית עצלה ממומשת בדומה לערמה, אך היא לא משמרת את המבנה כל הזמן: בפעולות הכנסה ומיזוג פשוט משרשרים את האיבר החדש או הערימה החדשה לקיימת (ב-) ואילו בפעולת המחיקה מתקנים תוך כדי את הערימה לערימה בינומית תקינה, פעולה זאת לוקחת , אך בניתוח לשיעורין עלותה הוא .
ערימת פיבונאצ'י
בערימת פיבונאצ'י העצים כלל אינם עצים בינומיים: בכל פעולת הקטנת הערך חותכים את הצומת ויוצרים ממנו עץ חדש, וכאשר מוחקים כך שני בנים של צומת חותכים גם אותו. כתוצאה מכך העלות של פעולת הקטנת המפתח עולה ל-, אך עלותה לשיעורין יורדת ל-. בשל כך היא טובה לאלגוריתמים שדורשים הקטנות רבות של המפתחות (כדוגמת אלגוריתם דייקסטרה שבערימת פיבונאצ'י סיבוכיותו היא לעומת בערימה בינארית).
הערות שוליים
- ↑ O(1) - בניתוח לשיעורין עבור n הכנסות רצופות בדומה למונה בינארי
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • X-fast trie • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |
ערימה בינומית31076454Q864032


