משפט ניקומאכוס
משפט ניקומאכוס הוא משפט בתורת המספרים הקובע כי הזהות הבאה מתקיימת לכל מספר טבעי n:
כלומר שסכום n המספרים המעוקבים הראשונים (חזקות שלישיות) שווה לריבוע סכום n המספרים הראשונים. המשפט קרוי על שם המתמטיקאי היווני בן המאה ה-1, ניקומאכוס, שכתב אודותיו.
היסטוריה
הזהות של ניקומאכוס נתגלתה באופן בלתי תלוי פעמים רבות במהלך ההיסטוריה. בין השאר גילו אותה ההודי אריאבהטה (המאה ה-5), הפרסי אל-קאראג'י (המאה ה-10), היהודי צרפתי רלב"ג (המאה ה-14) וההודי נילקנטה סומיאג'י (המאה ה-15).
תיאור המשפט
מבחינה פורמלית משפט ניקומאכוס קובע שלכל n טבעי מתקיים:
סכום המספרים הטבעיים מ-1 עד n נקרא המספר המשולשי ה-n, והוא מסומן . ישנה נוסחה מפורשת למספרים משולשיים: , ובאמצעותה ניתן לתאר את משפט ניקומאכוס גם כך:
הוכחות
למשפט ניקומאכוס הוכחות רבות. קודם להצגתן נציין שלוש זהויות שישמשו לשם קיצור ואסתטיות. את שלוש הזהויות ניתן להוכיח בפשטות בדרך אלגברית מתוך הנוסחה המפורשת למספר משולשי. עם זאת, לכולן ישנן גם הוכחות גאומטריות וקומבינטוריות.
- (נובע ישירות מההגדרה של מספר משולשי)
- (הוכחה קומבינטורית; לפשר הסימון ראו מקדם בינומי)
כמו כן נניח כי (כפי שאכן משתמע מכל הנוסחאות והזהויות).
הוכחה באינדוקציה
ההוכחה הסטנדרטית למשפט היא באינדוקציה. בסיס האינדוקציה הוא המשוואה . נניח כי ונראה כי :
נציב את הנחת האינדוקציה ואת הנוסחה למספר משולשי ונקבל:
כנדרש.
הוכחה באמצעות טור טלסקופי
נבחין בזהות הבאה הנובעת מזהויות (1) ו-(2):
כעת נוכל להציג את הסכום המבוקש כטור טלסקופי:
הוכחה קומבינטורית
נגדיר קבוצה שאיבריה הם רביעיות סדורות של מספרים בין 0 ל-n (כולל), כך שהאיבר הרביעי בכל רביעייה גדול ממש משלושת האיברים האחרים. בסימונים: . לכל k קבוע, h, i ו-j נבחרים בחופשיות מבין המספרים מ-0 עד k-1. כלומר יש רביעיות כאלו. ובסך הכל בכל הקבוצה A מספר האיברים הוא:
נגדיר עתה קבוצה שאיבריה הם זוגות סדורים של תת-קבוצות בנות שני איברים של קבוצת המספרים מ-0 עד n. כל תת-קבוצה כזו ניתן לאפיין למעשה כזוג סדור עם המגבלה שהאיברים בזוג שונים והגדול יותר נמצא בימין. כלומר:
B מורכבת מזוגות של תת-קבוצות עם שני איברים הנבחרים בחופשיות, ולכן מהגדרת המקדם בינומי ומזהות (3) נובע:
כעת נציג התאמה חד-חד-ערכית ועל מ-A ל-B:
הפונקציה בוודאי חד-חד-ערכית, והיא על כי לכל זוג סודר חוקי ניתן לבנות רביעייה מתאימה.
ההתאמה מעידה כי שתי הקבוצות שוות בגודלן, כלומר:
הוכחה גאומטרית
בספר "Proofs Without Words" (מסת"ב 978-0-88385-700-7) מובאות שבע הוכחות גאומטריות שונות למשפט. אחת מהן מודגמת באיור הבא:
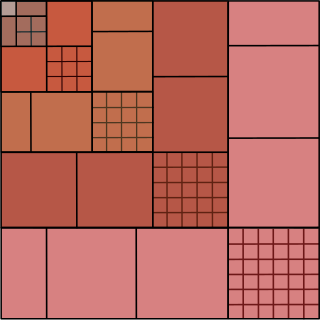
בכל צבע צבועים ריבועים עם צלע באורך . כלומר כל צבע מכסה שטח השווה ל- (כאשר במקרים הזוגיים אחד הריבועים מפוצל לשניים). כאשר מסדרים את כל השטחים יחדיו לכל נוצר ריבוע עם צלע באורך , ולכן שטחו .
הוכחה נוספת
ראשית נבחין בכך ש- הוא הסכום של מספרים אי-זוגיים עוקבים שהממוצע החשבוני שלהם הוא . פורמלית: .[1]
כעת נבחן את סכום האי-זוגיים מ-1 עד :
למשל סכום האי זוגיים מ-1 עד 19 הוא:
מצד שני את סכום האי-זוגיים מ-1 עד ניתן לחשב בעזרת הנוסחה לסכום טור חשבוני (או באמצעות טיעון גאומטרי) ולקבל שהוא שווה ל- כנדרש.
הכללות
יאקוב ברנולי מצא נוסחה כללית לחישוב סכום חזקות כלשהן של n המספרים הראשונים:
כאשר הוא מספר ברנולי ה-i.
כאשר m אי-זוגי, הסכום הוא תמיד פולינום, ללא מקדם חופשי, ב-.
קישורים חיצוניים
- שתי הוכחות קומבינטוריות של (באנגלית)
- סכימת מספרים מעוקבים באמצעות ספירת מלבנים (באנגלית)
- הוכחה גאומטרית (באנגלית)
- משפט ניקומאכוס, באתר MathWorld (באנגלית)
הערות שוליים
- ↑ בסכום יש מחיבורים (זהות (1)) והממוצע שלהם הוא אכן (זהות (2)) כנדרש.
משפט ניקומאכוס41373013Q2197859


