מי שהיה נשוי שלוש נשים

מי שהיה נשוי שלוש נשים
(מקורות עיקריים)
משנה	מסכת כתובות, פרק י', משנה ד'
תלמוד בבלי	מסכת כתובות, דף צ"ג עמוד א'
תלמוד ירושלמי	מסכת כתובות, פרק י', הלכה ד'
משנה תורה	הלכות אישות, פרק י"ז, הלכה ח'
שולחן ערוך	אבן העזר, סימן צ"ו, סעיף י"ח

מי שהיה נשוי (ל)שלוש נשים הוא משפט הפתיחה של משנה בסדר נשים, מסכת כתובות, פרק י', משנה ד', העוסקת בחלוקת רכוש בין מספר נשים. המשנה דנה בדוגמה של חלוקת עזבונו של אדם בין שלוש אלמנותיו, אולם מציינת שאותו הכלל תקף גם למקרים כגון פירוק שותפות. במשנה מוצג אופן החלוקה בשלושה מקרים שבהם העיזבון אינו גדול דיו כדי לכסות את הסכום שהובטח בכתובה לכל אחת מהנשים. התלמוד ובעקבותיו פרשני המשנה התקשו למצוא את הכלל המנחה שעל פיו נקבעו מקרים אלו, ונזקקו להוסיף תנאים לדיני המשנה, כך שהמשנה נותרה ללא פירוש פשוט. בשנת 1985 הציעו ישראל אומן ומיכאל משלר פתרון אפשרי לבעיה, שמבוסס על הכללת שיטת החלוקה שמתוארת במשנת שניים אוחזין, הפותחת את מסכת בבא מציעא. הפתרון הוא יוצא דופן בכך שהוא התגלה באמצעות הפעלת כלים מתורת המשחקים המודרנית (תחום מומחיותם של אומן ומשלר), על טקסט מן המשנה.

תיאור המשנה

מִי שֶׁהָיָה נָשׂוּי שָׁלשׁ נָשִׁים וּמֵת, כְּתֻבָּתָהּ שֶׁל זוֹ מָנֶה וְשֶׁל זוֹ מָאתַיִם וְשֶׁל זוֹ שְׁלֹשׁ מֵאוֹת, וְאֵין שָׁם (בעיזבונו) אֶלָּא מָנֶה, חוֹלְקוֹת בְּשָׁוֶה.
הָיוּ שָׁם מָאתַיִם, שֶׁל מָנֶה נוֹטֶלֶת חֲמִשִּׁים; שֶׁל מָאתַיִם וְשֶׁל שְׁלֹשׁ מֵאוֹת, שְׁלֹשָׁה שְׁלֹשָׁה שֶׁל זָהָב.
הָיוּ שָׁם שְׁלֹשׁ מֵאוֹת, שֶׁל מָנֶה, נוֹטֶלֶת חֲמִשִּׁים; וְשֶׁל מָאתַיִם, מָנֶה; וְשֶׁל שְׁלֹשׁ מֵאוֹת, שִׁשָּׁה שֶׁל זָהָב.
וְכֵן שְׁלֹשָׁה שֶׁהִטִּילוּ לְכִיס (השקיעו בשותפות), פִּחֲתוּ אוֹ הוֹתִירוּ, כָּךְ הֵן חוֹלְקִין:

— משנה, מסכת כתובות, פרק י', משנה ד'

המשנה אינה מתייחסת לסדר קדימויות כלשהו שעשוי להתקיים בין הנשים (למשל, כזה שנקבע על פי הסדר שבו נישאו לנפטר), ועל כן החלוקה שמוצגת בה מתבססת אך ורק על גודל הכתובה של כל אחת מהנשים. שוויו של ה"מנה" הוא מאה דינרי כסף, ושוויו של דינר זהב הוא 25 דינרי כסף. סיכום של המשנה מופיע בטבלה הבאה, המציגה את חלקה של כל אישה בהתאם לסכום שבכתובּתה ולגודל העיזבון:

		סכום הכתובה
		$100$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}
גודל העיזבון	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	$33{\frac {1}{3}}$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 50}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 75}	$75$
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 50}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 150}

העיקרון הכללי שמנחה את החלוקה אינו ברור. כאשר גודל העיזבון הוא 100 דינרים, מתבצעת חלוקה שווה – כל אחת מהנשים מקבלת אותו הסכום מהעיזבון. כאשר גודל העיזבון הוא 300, מתבצעת לכאורה החלוקה על פי כלל אחר – כל אישה מקבלת סכום השקול לגודלה היחסי של כתובתה. במקרה שבו גודל העיזבון הוא 200, לא ברור אם יש כלל פשוט שיסביר את החלוקה המתקבלת, שבה מקבלות שתי הנשים בעלות הכתובה הגבוהה יותר סכום זהה, הגדול מזה של בעלת הכתובה הקטנה יותר.

ההסבר בתלמוד ובפרשניו

התלמוד הבבלי (מסכת כתובות, דף צ"ג עמוד א') מתקשה בהסברה של המשנה, ומעמיד אותה כמתקיימת במקרים חריגים בלבד. השיטה הבסיסית לחלוקה היא פריסת השעבודים לפי הזכויות. על המאה הראשונה יש שעבוד לבעלות שלוש הכתובות, על המאה השנייה יש שעבוד לבעלות הכתובה בת ה-200 והכתובה בת ה-300, ועל המאה השלישית יש שעבוד לבעלת הכתובה בת ה-300 בלבד. כל חלק מתחלק באופן שווה בין כל הנשים שמשעבדות אותו.

ניתן להמחיש את צורת החלוקה לפי עיקרון זה בטבלה הבאה:

		סכום הכתובה
		הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	$200$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}
גודל העיזבון	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}
	$200$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 83\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 83\frac{1}{3}}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 83\frac{1}{3}}	$183{\frac {1}{3}}$

צורת חלוקה זו אינה תואמת את הנאמר במשנה ולכן חכמי התלמוד העמידו שתי אוקימתות לדין האמור במשנה. שיטתו של האמורא שמואל היא שהדין אמור רק במקרים שבהם בעלת אחת הכתובות מוותרת לשנייה על הסכום שזו תובעת. רב יעקב מנהר פקוד מביא בשמו של רבינא את הדעה שהמשנה עוסקת במקרה שבו האלמנות חילקו נכסים שנפלו לפניהן בשני זמנים שונים ("בשתי תפיסות"), כך שהדיון אינו נערך בבת אחת, אלא כל פעם על סכום אחר. בסופו של הדיון מובאת ברייתא בה נאמר שדין המשנה אינו מוסכם, ודעתו של רבי יהודה הנשיא (המכונה בה 'רבי'), היא שיש לערוך חלוקה שווה בשווה: ”תניא: זו משנת רבי נתן. רבי אומר: אין אני רואה דבריו של רבי נתן באלו, אלא חולקות בשוה.”.

פירוש המשנה עורר קושי גם בין פרשני המשנה והתלמוד המאוחרים יותר, שהתקשו למצוא לה הסבר המניח את הדעת כשלעצמו מחד, ומתיישב עם דברי התלמוד מאידך. לדוגמה, הרי"ף, שבדרך כלל מסתפק בציטוט מתומצת של קטע הגמרא הנפסק להלכה, הקדיש לסוגיה שלושה עמודים, ופתח במילים ”הא מתניתין וגמרא דילה שקלי וטרו בה קמאי ז"ל, ולא סלקא להון כל עיקר” ("משנה זו והגמרא שלה נשאו ונתנו בה הקדמונים ז"ל, ולא עלתה בידם כל עיקר").

לעומת זאת, רס"ג כתב, בהתייחסו לניסיון אחר להסביר את המשנה שלא לפי העמדת התלמוד, שההלכה אומנם נפסקת לפי התלמוד, אך אין מניעה לפרש את המשנה בניגוד אליו.^[1]

שתי שיטות הראשונים בהסבר שיטת רבי

השיטה שנתקבלה להלכה היא שיטת רבי, ובהבנתה יש שתי פרשנויות. הפרשנות של הרי"ף ושל הרמב"ם^[2] השולחן ערוך^[3] ועוד היא שהחלוקה נעשית באופן שווה מבחינה מספרית, עד למצב בו אחת הנשים מקבלת את מלא כתובתה. ניתן להמחיש זאת בטבלה הבאה:

		סכום הכתובה
		הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}
גודל העיזבון	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	$33{\frac {1}{3}}$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 66\frac{2}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 66\frac{2}{3}}	$66{\frac {2}{3}}$
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 400}	$100$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 150}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 150}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 550}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 250}

לעומת זאת, יש הסוברים שבאופן זה "מידת הדין לוקה", כיון שבעלת הכתובה הקטנה יותר אינה מפסידה באחוזים זהים להפסד של בעת הכתובה המרובה. לכן, לשיטת רבנו חננאל החלוקה נעשית לפי אחוזים, מצרפים את כלל הכתובות לסכום, משווים לסכום שנשאר בעיזבון, והאחוזים שניתן לגבות ממנו ניתנים לבעלות הכתובות^[4]. ניתן להמחיש את שיטת החלוקה הזו בטבלה הבאה:

		סכום הכתובה
		הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}
גודל העיזבון	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 16\frac{2}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 50}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 33\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 66\frac{2}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 50}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 150}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 400}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 66\frac{2}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 133\frac{1}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 200}
	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 500}	$83{\frac {1}{3}}$	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 166\frac{2}{3}}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 250}

הקבלה לשנים אוחזים

לכאורה, ניתן להשוות את דין המשנה לדין שניים אוחזין בטלית שמופיע במשנה הפותחת את מסכת בבא מציעא. במשנה זו נאמר:

”שנים אוחזין בטלית... זה אומר: כולה שלי. וזה אומר: חציה שלי... זה נוטל שלשה חלקים, וזה נוטל רביע” (משנה, מסכת בבא מציעא, פרק א', משנה א')

המקור הקדום ביותר לניסיון הקבלת דין המשנה לדין שניים אוחזין נמצא ברי"ף. לדבריו, רב האי גאון סבר ששתי המשניות מבוססות על כלל אחד, אך הוא שמע שחזר בו בסוף ימיו.
בנספח שכתב הרי"ף בערבית, חלק הרי"ף על דעתו, משום שחלוקת הרכוש שוה בשוה על ידי שבועה נכונה במקרה שבו קיים ספק למי שייך הרכוש, והנתונים היחידים הם טענותיהם של המחזיקים, בשונה מהנידון שלפנינו, שבו העובדות ידועות, והשאלה היא רק איך לחלק את הממון הבלתי מספיק. בנוסף, הרי"ף היקשה על הקבלה זו מתוך דברי התלמוד: לפי הברייתא במסכת כתובות, רבי יהודה הנשיא חולק על משנת שלוש הנשים, בעוד שבסוגיית שניים אדוקים בשטר^[5] התלמוד מניח שהוא אינו חולק על משנת שניים אוחזין, לכן הסיק הרי"ף ששתי המשניות אינן מבוססות על כלל אחד.

שיטתם של אומן ומשלר

ישראל אומן החל לעסוק במשנה לאחר שבנו שלמה הביא אותה לתשומת לבו, בעת דיון שניהלו השניים על מאמר^[6] שעסק במספר בעיות תלמודיות אחרות^[7]. אומן יחד עם מיכאל משלר, ניסה לפתור את הבעיה באמצעות כלים מתורת המשחקים, שלא היו זמינים למפרשי התלמוד וסייעו לשפוך אור חדש על הבעיה. התברר כי החלוקה שמוצגת במשנה תואמת את אחת משיטות הפתרון שבהן עוסקת תורת המשחקים השיתופיים – שיטה המבוססת על מושג הנקרא "גרעינון של משחק". אף שהמושג מורכב למדי ולא סביר שהיה מוכר בכלליותו לתנאים, ניתוח התכונות שלו סייע במציאת העיקרון שלדעתם הנחה את המשנה.

בשנת 1985 פרסמו אומן ומשלר מאמר בכתב העת Journal of Economic Theory ובו הציגו את הבעיה והציעו לה פתרון,^[8] אשר מתבסס על שיטת החלוקה שהובאה לעיל, המוצגת במשנת "שניים אוחזין"^[9].

כאן מוצג מקרה פשוט יותר, שניתן לראותו כעוסק בחלוקת רכוש בין שני טוענים. כלל החלוקה במקרה זה הוא של חלוקה שווה של הסכום השנוי במחלוקת: האדם שטוען לבעלות על מחצית מהטלית מסכים כי המחצית השנייה שייכת לאדם השני, ולכן הסכום השנוי במחלוקת במקרה זה הוא רק מחצית הטלית. מחצית זו מחולקת שווה בשווה בין שני הטוענים – וכך האחד נותר עם רבע טלית, והשני עם שלושת רבעי טלית.

אומן ומשלר שמו לב לכך שהחלוקה המוצעת במשנה עבור שלוש הנשים מקיימת את התכונה הבאה: לכל זוג אלמנות מתקיימת חלוקה על פי כלל "שניים אוחזין", כאשר מחלקים ביניהן את הסכום שנותר לאחר שהאלמנה השלישית קיבלה את חלקה. בניסוח חלופי: הסכום שמקבלת כל אשה מתאים לכך שהסכום הנשאר מתחלק בין השתיים הנותרות על פי כלל "שניים אוחזין".

למשל, במקרה שבו גודל העיזבון הוא 200 דינרים, אם נותנים לאלמנה השלישית את הסכום שהובטח לה בחלוקה בהתאם למשנה (75) נותרים עם סכום של 125 לחלק בין שתי הנותרות. מכיוון שהאישה הראשונה תובעת סכום של 100 והשנייה סכום של 200, ישנם 25 דינרים שאינם שנויים במחלוקת (האישה הראשונה מסכימה שהם שייכים לאישה השנייה) ולכן על פי שיטת "שניים אוחזין", 100 הדינרים השנויים במחלוקת יתחלקו שווה בשווה בין שתי הנשים. לכן הראשונה תקבל 50 והשנייה תקבל בסך הכול 75 – בדיוק כפי שמוצג בטבלה.

בדומה, אם נותנים לאלמנה הראשונה את הסכום שהובטח לה בחלוקה בהתאם למשנה – 50 דינרים – נותרים עם סכום של 150 לחלק בין שתי הנותרות. במקרה זה כל הסכום שנוי במחלוקת (כי האחת דורשת 200 והשנייה 300) ולכן כולו יתחלק שווה בשווה, ושוב תתקבל אותה החלוקה שכבר כתובה בטבלה. לא קשה לראות כי תכונה זו מתקיימת לכל זוג אפשרי מתוך הטבלה.

בעקבות גילוי זה הגדירו אומן ומשלר חלוקה כתואמת שניים אוחזין אם התכונה הזו מתקיימת עבורה – כלומר, אם לכל זוג נושים, הסכום שנותר מתחלק ביניהם על פי שיטת שניים אוחזין (במילים אחרות, אם הסכום שמקבל כל נושה מתאים לכך שהסכום הנשאר מתחלק בין כל זוג מבין כל שאר הנושים על פי כלל "שניים אוחזין"). הם הוכיחו כי לכל גודל של עיזבון ולכל מספר של נושים קיימת חלוקה שהיא תואמת שניים אוחזין, וכי החלוקה הזו היא יחידה, דהיינו אין שתי חלוקות שונות עבור אותו עיזבון ואותם נושים ששתיהן בעלות התכונה של "תואמת שניים אוחזין". כמו כן, הם הציעו שיטה לחשב אותה באופן מעשי.

המחשת שיטת החלוקה והוכחת תכונותיה

קובץ:ThreeWives1.png

חלוקת העיזבון בין שתי נשים במקרה א': העיזבון קטן מכל אחת מהכתובות, ולכן הנוזל אינו מגיע אף לחצי מקיבול כל אחד מהכלים

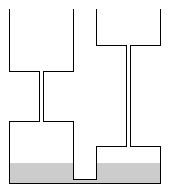
ניתן להמחיש בצורה ויזואלית את שיטת החלוקה, כמו גם להוכיח את תכונותיה, באמצעות חוק הכלים השלובים.

לכל אישה יש כלי משלה, אשר הקיבולת שלו שקולה לגודל הכתובה של האישה. הכלים כוללים שני חלקים (עליון ותחתון) שווים בגודלם המחוברים ביניהם בצינורית דקה בעלת קיבולת זניחה. הכלים של כל הנשים הם בעלי גובה ורוחב שווים ונבדלים בגובה הצינורית הדקה (ראו איור). הכלים מחוברים זה לזה בתחתיתם בצינורית דקה בעלת קיבולת זניחה, כך שנוזל המוכנס אליהם יתחלק לפי עקרון הכלים השלובים. כמות הנוזל שמוכנס לכלים שקול לגודל העיזבון וגובהו יהיה שווה בכל הכלים. הנוזל יתחלק בהתאם לכלל של המשנה, כך שכל אישה תקבל בדיוק את המגיע לה.

נדון קודם במקרה בו ישנן שתי נשים בלבד, מכיוון שבעזרתו ניתן להוכיח את המקרה הכללי. נפריד בין שלושה מקרים אפשריים:

מקרה א'

במקרה א', העיזבון קטן יותר מכל אחת מהכתובות של הנשים. באיור הדבר מתבטא בכך שגובה פני הנוזל לא מגיע אף למחצית הכלי הקטן יותר, ועל כן הוא מתחלק באופן שווה בין הכלים, בהתאם לכלל שנגזר ממשנת "שניים אוחזין" עבור המקרה שבו כל הסכום שנוי במחלוקת.

החלוקה השווה של הנוזל בין הכלים נפסקת כאשר מתמלא חלקו התחתון של הכלי הקטן, ונותר עוד נוזל לחלוקה. זה קורה כאשר הכמות הכוללת של הנוזל גדול מהקיבול של הכלי הקטן כולו – כלומר, כאשר גודל העיזבון גדול מהכתובה הקטנה יותר.

מקרה ב'

שגיאה ביצירת תמונה ממוזערת:

חלוקת העיזבון בין שתי נשים במקרה ב': שני המקרים האפשריים מוצגים

במקרה ב', העיזבון גדול מהכתובה של האישה הראשונה, אך קטן מהכתובה של האישה השנייה. כאן ניתן להבחין בשני מצבים שונים בכלים השלובים:

בכלי הגדול יותר, הנוזל לא ממלא את כל חציו התחתון וגם לא נוגע כלל בחציו העליון. אבל בכלי הקטן הוא ממלא לחלוטין את החצי הראשון אך עדיין לא מתחיל להיכנס לחצי השני. (צד שמאל בתרשים)
הכלי הגדול מתחיל להתמלא גם בחציו העליון, בעוד הכלי הקטן מלא רק עד חציו הראשון. (צד ימין בתרשים)

בכל המקרים הללו העיקרון דומה: כל הנוזל שמתווסף בשלב זה מתווסף רק לכלי הגדול יותר (שכן בכלי הקטן יותר הדבר היחיד שמתמלא הוא הצינורית, שאנו מניחים שמכילה כמות זניחה של נוזל).

הדבר מתאים לחלוקה שאמורה להתקיים בשלב זה: העיזבון גדול מהכתובה של האישה הראשונה, והיא אינה מתייחסת לסכום הנוסף כאל סכום שנוי במחלוקת, ולעומת זאת האישה השנייה תובעת גם אותו, ולכן כולו הולך אל האישה השנייה.

מקרה ג'

שגיאה ביצירת תמונה ממוזערת:

חלוקת העיזבון בין שתי נשים במקרה ג'.

המקרה השלישי הוא המורכב מבין השלושה. כאן העיזבון הכולל גדול הן מהדרישה של האישה הראשונה והן מהדרישה של האישה השנייה (אך עדיין אינו גדול מספיק כדי לכסות את הדרישות של שתי הנשים גם יחד). בתור דוגמה ניתן להתבונן במצב בו שתי הכתובות הן בסך 100 ו-150, ואילו העיזבון הוא בגודל 200. במקרה זה האישה הראשונה (הקו האדום באיור) דורשת 100 זוזים בלבד ולכן היא מוותרת לרעותה על ה-100 הנותרים, והשנייה (הקו הכחול באיור) לוקחת 150 בלבד ולכן מוותרת לרעותה על ה-50 הנותרים. לכן נותרו 50 זוזים בלבד השנויים במחלוקת (באיור: שטח החפיפה בין שתי הדרישות), שמחולקים שווה בשווה (והחלוקה המתקבלת היא 75 לראשונה, 125 לשנייה).

בדוגמה ניתן לראות כי ההפרש בין הכתובות הוא גם ההפרש בין החלוקה שבוצעה. זוהי תכונה כללית המאפיינת את מקרה ג': הסכום עליו מוותרת האישה השנייה לרעותה הוא ההפרש בין הכתובות של שתיהן, ואילו שאר הסכום (השנוי במחלוקת) מתחלק ביניהן שווה בשווה. כלומר, גודל ההפרש בין מנת החלוקה שתקבל האישה הראשונה ומנה שתקבל האישה השנייה שווה בגודלו לסכום שעליו ויתרה האישה השנייה.

קל לראות כי תכונה כללית זו – ההפרש בין הכתובות הוא ההפרש בין המנות – מתקיימת גם עבור הכלים: ההפרש בין כמות הנוזלים שבשני הכלים הוא בדיוק ההפרש המקורי בנפח שלהם, שבא לידי ביטוי בחלק האמצעי של הכלים (שבו יש צינורית בלבד עבור הכלי הקטן יותר, אך חלק מכלי הקיבול עבור הכלי הגדול יותר). הסיבה לכך היא שהחלק העליון של שני הכלים זהה ברוחבו, ולכן מרגע שחלק זה התחיל להתמלא בשני הכלים, כל תוספת נוזל תתחלק שווה בשווה בין שניהם.

החלוקה במקרה הכללי

שגיאה ביצירת תמונה ממוזערת:

דוגמה לחלוקת העיזבון כאשר יש ארבע נשים שלכל אחת כתובה בגודל שונה

הכללה של הבעיה, שבה יש קבוצה מגודל כלשהו של נשים שלכל אחת כתובה משל עצמה, אינה שונה בבסיסה מהמקרה הפרטי של שתי נשים.

כדי להיווכח כי החלוקה שנוצרת על ידי הכלים היא אכן "תואמת שניים אוחזין", די לראות כי אם בוחנים כל זוג כלים בנפרד ומנתקים אותו מהיתר, שני הכלים מתאימים לאחד משלושת המקרים שתוארו למעלה, ולכן מצייתים לכלל "שניים אוחזין". יתר על כן, ברור כי החלוקה שמושרית על ידי הכלים היא החלוקה היחידה שמקיימת את התכונה הזו – בכל חלוקה אחרת גובה פני הנוזל לא יהיה אחיד לכל הכלים, וכשנבחן זוג כלים שבו פני הנוזל אינם באותו הגובה נקבל שבזוג כלים זה החלוקה אינה על פי "שניים אוחזין".

תיאור פורמלי של שיטת החלוקה

אף שההמחשה באמצעות חוק הכלים השלובים שהוצגה קודם מסייעת רבות להבנת הפתרון, היא אינה מאפשרת ישירות את ביצוע החישוב שמוצא, בהינתן אוסף כתובות וגודל עיזבון, את החלוקה המבוקשת. להלן אלגוריתם שעושה זאת:

האלגוריתם מפריד בין שני מקרים – במקרה הראשון, העיזבון קטן יותר ממחצית סכום כל הכתובות, ובשני הוא גדול יותר. במקרה הראשון מתחילים ממצב בו "הכלים ריקים" – אף אישה לא קיבלה דבר. בכל סיבוב של האלגוריתם, מחולק זוז נוסף מהעיזבון שווה בשווה בין כל הנשים, עד אשר חולק לכל אחת מהנשים סכום השווה למחצית הכתובה של האישה בעלת הכתובה הקטנה ביותר (כלומר, החצי התחתון של הכלי שלה התמלא). לאחר מכן ממשיכים את החלוקה שווה בשווה בין שאר הנשים עד אשר מחולק להן סכום השווה למחצית הכתובה השנייה בקוטנה, ואז מוציאים גם אותה מהחלוקה, וכן הלאה.

הטיפול במקרה השני דומה, אלא שבמקרה זה מתחילים ממצב בו "הכלים מלאים" – כל הנשים קיבלו את כל כתובתן, ומתחילים לחסר מהן שווה בשווה, כאשר מפסיקים לחסר מאישה שהגיעה למחצית כתובתה.

ההתנגדות לשיטת אומן

בקובץ 'בית אהרון וישראל' פורסמו בשנת תשס"ז (2007) שני מאמרים,^[10] מאת הרבנים שלום מרדכי סגל ונתן פרלמן, המתנגדים לשיטת אומן בהסבר המשנה. עיקר טענותיהם:

הטענה הראשונה: אין לדמות את סוגייתנו לסוגיית "שניים אוחזים" ולכן אין להשתמש בעקרון החלוקה של "שניים אוחזים" כאן. במשנת "שניים אוחזים" כל אחד מהצדדים הטוען לבעלות על החפץ טוען שאין לצד השני חלק בחלק עליו הוא טוען לבעלות. החלק אותו שני הצדדים חולקים הוא חלק שכל אחד טוען שאינו שייך לשני. במשנתנו אין ויכוח בין הנשים לגבי עצם הזכות שלהן בירושה, כל אחת מודה שמגיע לשנייה את חלקה בכתובה, אמנם הדיון הוא כיצד לחלק את הכתובה במקרה שאין בירושה את כל הסכום.
הטענה השנייה: גם במקרה של ויכוח על בעלות (שלדעת הכל יש לו דין של משנת "שניים אוחזים") בין שלושה, הדין אינו כפי שהציע פרופ' אומן, אלא כפי שיטת המהרי"ל דיסקין בדיני "שלושה אוחזים".^[11]
הטענה השלישית: לא ייתכן לתת למשנה הסבר שלא על פי ההבנה של הגמרא, יתר על כן לשיטת אומן, הפירוש הנכון במשנה נעלם מעיני חכמי התלמוד. הגמרא בעצמה לא מצאה הסבר אחיד בהבנת דברי המשנה ולכן העמידה את המשנה באוקימתות, כיצד ייתכן להביא הסבר שיפרש את דברי המשנה כביכול כפשוטן, אך בשונה ממה שהעלתה הגמרא על דעתה.

תשובותיו של אומן לטענות אלו

אומן התייחס לטענות נגדו בקובץ 'המעיין' שנת תש"ע (2010).^[12]

לגבי הטענה הראשונה: אומן מוכיח שעיקרון זה מיושם במספר מקומות בתלמוד גם במקרים בהם אין ויכוח בין שני צדדים. כמו כן טוען אומן כי כבר היו מהגאונים שניסו להסביר את משנתנו לפי עקרון "שניים אוחזים".
לגבי הטענה השנייה: אכן, טוען אומן, אין ליישם את שיטת המשנה להלכה במקרה של שלושה אוחזים כיוון שאכן משנה זו לא התקבלה להלכה אלא ההלכה היא כשיטת רבי.
לגבי הטענה השלישית: כותב אומן שהטוענים לא הבינו את דבריו בהסבר הגמרא. שיטתו אינה מנסה להביא הסבר אחר נוסף לגמרא. אלא שלשיטתו לאחר שהובאה בגמרא שיטת רבי, חוזרת הגמרא להסביר את המשנה כפשוטה. טענה זו כתובה לדברי אומן בדברי רבנו חננאל בסוגיה.^[13]

ראו גם

שניים אוחזין בטלית

לקריאה נוספת

תורת חיים – פתרון חלוקת כתובה לשלוש נשים, ד"ר יחזקאל טאוב, סיון תשע"ט, קריית אתא.

קישורים חיצוניים

מחשבון חלוקה צודקת על-פי שיטת אומן ומשלר ושיטות נוספות.
מי שהיה נשוי שלוש נשים, המשנה והגמרא בתלמוד הבבלי, מתוך אתר ויקיטקסט
מי שהיה נשוי שלוש נשים, המשנה והגמרא בתלמוד הירושלמי, מתוך אתר ויקיטקסט
בעניין מי שהיה נשוי שלוש נשים – מאמר לא טכני של אומן המיועד לקהל הלמדני. מתוך: מוריה, שנה כב, גיליון ג–ד (רנה–רנו), טבת תשנ"ט, עמ' צח–קז
תורת המשחקים ודיני פשיטת רגל, באתר "דעת", עיבוד למאמרו של אומן מתוך: משפט עברי, גיליון 234, תשס"ו
המאמר המתמטי המקורי של אומן ומשלר
אורי ניצן, אשה אחת מקבלת 75 זוז, אשה שנייה מקבלת 50 – וזה מדעי, באתר הארץ, 9 ביולי 2002
פרופ' ישראל אומן, כתובות צג. – שלש האלמנות וכתובתן, באתר "כולל עיון הדף"
פרופ' ישראל אומן, "מי שהיה נשוי שלוש נשים" – סוגיא במסכת כתובות דף צג ע"א, באתר של מכון מאיר
גדי אלכסנדרוביץ', מי שהיה נשוי שלוש נשים, באתר "לא מדויק", 22 בספטמבר 2008
אליהו סולובייצ'יק, על הדרך הנאותה בפרשנות משנת 'מי שהיה נשוי שלש נשים', באתר דאצ'ה
פרופ' ישראל אומן, עוד על שלוש הנשים: הערות למאמרי ביקורת, באתר דאצ'ה
הרצאה של פרופ' אומן בערוץ . חלק א', חלק ב'
אליהו סולובייצ'יק, ‏שלש נשים - מאמר תגובה, המעין תמוז תש"ע
יעקב לויפר, ‏חלוקת שלש הכתובות - תגובה, המעין תמוז תש"ע
ישראל אומן, ‏בענין מי שהיה נשוי שלוש נשים: חלק שני ותשובה למשיבים, המעין תמוז תש"ע
הרב יוסף שריקי, 'מי שהיה נשוי שלוש נשים' – ביאור שיטות רב האי גאון והרי"ף; ותגובת פרופ' ישראל אומן, המעין, ניסן תשע"ח
מידע על מי שהיה נשוי שלוש נשים בקטלוג הספרייה הלאומית

הערות שוליים

^ ”אף על פי שיודעין אנו שהלכה כרבי ולא כר' נתן ואע"פ ששמואל מעמידה בכותבת זו לזו ולפצותה מדין ודברים וכי רב יעקב משמיה דרבינא מעמידה בשתי תפישות אעפ"כ מקום הניחו לנו גם אנו ויכולנו להעמידה בתנאי ב"ד על הממון הנמצא למת” (תשובת רס"ג המובאת באוצר הגאונים, מסכת כתובות, סימן תשכ"א)
^ ראו משנה תורה לרמב"ם, הלכות אישות, פרק י"ז, הלכה ח'
^ ראו בשולחן ערוך, אבן העזר, סימן צ"ו, סעיף י"ח
^ ראו בתוספות, מסכת כתובות, דף צ"ג עמוד א', ד"ה רבי. הרמב"ם הזכיר שיטה זו במשנה תורה לרמב"ם, הלכות מלווה ולווה, פרק כ', הלכה ד' בשם "יש מן הגאונים".
^ תלמוד בבלי, מסכת בבא מציעא, דף ז' עמוד א'
^ O'Neill, Barry (1982). "A problem of rights arbitration from the Talmud". Mathematical Social Sciences. Elsevier BV. 2 (4): 345–371. doi:10.1016/0165-4896(82)90029-4. ISSN 0165-4896.
^ בשיעור בישיבת ברכת משה פרופ' אומן הדגיש שהמקור למאמר של O'Neill היה עבודתו של הרב נחום אליעזר רבינוביץ' על סבירות והסתברות בספרות חז"ל והראשונים.
^ Robert J Aumann, Michael Maschler, Game theoretic analysis of a bankruptcy problem from the Talmud, Journal of Economic Theory, Volume 36, Issue 2, August 1985
^ כאמור, שיטה זו נדחתה על ידי הרי"ף
^ קובץ בית אהרן וישראל, ירושלים תשס"ז, גיליון קכז (שנה כב גיליון א) עמ' מח ואילך; שם, גיליון קכט (שנה כב גיליון ג) עמ' קכא ואילך
^ קובץ תורה מציון שנה ראשונה, תרמ"ז, סימן ל"ב
^ פרופ' ישראל אומן, ‏תגובה בעניין מי שהיה נשוי שלוש נשים, המעין טבת תש"ע
^ שנה לאחר מכן, התפרסמה בארצות הברית, תגובה של המתנגדים להסבריו של אומן במאמר התגובה. ראו: ישעיה פלאם, על שלוש נשים, שנים אוחזין, חילוק אחד קטן וכבוד התורה, אור ישראל, גיליון סב, ניסן תשע"א, עמ' רצו–שה

ערך טוב

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

39172800מי שהיה נשוי שלוש נשים

[1] ”אף על פי שיודעין אנו שהלכה כרבי ולא כר' נתן ואע"פ ששמואל מעמידה בכותבת זו לזו ולפצותה מדין ודברים וכי רב יעקב משמיה דרבינא מעמידה בשתי תפישות אעפ"כ מקום הניחו לנו גם אנו ויכולנו להעמידה בתנאי ב"ד על הממון הנמצא למת” (תשובת רס"ג המובאת באוצר הגאונים, מסכת כתובות, סימן תשכ"א)

[2] ראו משנה תורה לרמב"ם, הלכות אישות, פרק י"ז, הלכה ח'

[3] ראו בשולחן ערוך, אבן העזר, סימן צ"ו, סעיף י"ח

[4] ראו בתוספות, מסכת כתובות, דף צ"ג עמוד א', ד"ה רבי. הרמב"ם הזכיר שיטה זו במשנה תורה לרמב"ם, הלכות מלווה ולווה, פרק כ', הלכה ד' בשם "יש מן הגאונים".

[5] תלמוד בבלי, מסכת בבא מציעא, דף ז' עמוד א'

[LTR-1982-6] O'Neill, Barry (1982). "A problem of rights arbitration from the Talmud". Mathematical Social Sciences. Elsevier BV. 2 (4): 345–371. doi:10.1016/0165-4896(82)90029-4. ISSN 0165-4896.

[7] בשיעור בישיבת ברכת משה פרופ' אומן הדגיש שהמקור למאמר של O'Neill היה עבודתו של הרב נחום אליעזר רבינוביץ' על סבירות והסתברות בספרות חז"ל והראשונים.

[8] Robert J Aumann, Michael Maschler, Game theoretic analysis of a bankruptcy problem from the Talmud, Journal of Economic Theory, Volume 36, Issue 2, August 1985

[9] כאמור, שיטה זו נדחתה על ידי הרי"ף

[10] קובץ בית אהרן וישראל, ירושלים תשס"ז, גיליון קכז (שנה כב גיליון א) עמ' מח ואילך; שם, גיליון קכט (שנה כב גיליון ג) עמ' קכא ואילך

[11] קובץ תורה מציון שנה ראשונה, תרמ"ז, סימן ל"ב

[12] פרופ' ישראל אומן, ‏תגובה בעניין מי שהיה נשוי שלוש נשים, המעין טבת תש"ע

[13] שנה לאחר מכן, התפרסמה בארצות הברית, תגובה של המתנגדים להסבריו של אומן במאמר התגובה. ראו: ישעיה פלאם, על שלוש נשים, שנים אוחזין, חילוק אחד קטן וכבוד התורה, אור ישראל, גיליון סב, ניסן תשע"א, עמ' רצו–שה

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

מי שהיה נשוי שלוש נשים

תוכן עניינים

תיאור המשנה