טרוכואיד

שגיאה ביצירת תמונה ממוזערת:

הציקלואידה, טרוכואיד נפוץ, נוצרת על ידי מיקום הנקודה הקבועה על היקף הגלגל וגלגולו על ישר.

הטרוכואיד (מהמילה היוונית לגלגל "trochos") הוא העקומה המתוארת על ידי נקודה קבועה על מעגל כאשר הוא מתגלגל על קו ישר. הציקלואידה משתייכת למשפחת העקומים הטרוכואידים. המונח טרוכואיד נטבע על ידי ז'יל פרסון דה רוברוואל.

תיאור בסיסי

כאשר מעגל ברדיוס a מתגלגל ללא החלקה לאורך ישר L, המרכז C נע במקביל ל-L, וכל נקודה אחרת P במישור הקשיח המסתובב עליו נח המעגל מתווה עקום הנקרא טרוכואיד. נניח ש-CP = b. המשוואות הפרמטריות המתארות את הטרוכואיד כאשר L הוא ציר ה-x הן:

$x=a\theta -b\sin(\theta )\,$

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = a - b \cos(\theta) \,}

כאשר θ הוא פרמטר השווה לזווית הסיבוב הכוללת אשר המעגל הסתובב.

טרוכואיד מכווץ, נפוץ, ומורחב

שגיאה ביצירת תמונה ממוזערת:

מהתרשים העליון לתחתון, טרוכואיד מרוחב, נפוץ, ומכווץ.

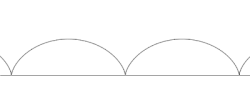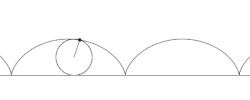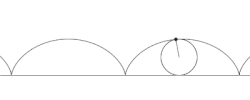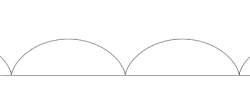
אם P נחה בתוך המעגל (b < a), על ההיקף שלו (b = a), או מחוצה לו (b > a), אז הטרוכואיד מתואר כמכווץ (curtate), נפוץ, או מורחב (prolate) בהתאמה. כיוון שהמעגל מתגלגל ללא החלקה, מהירות הסיבוב על היקפו שווה למהירות התקדמות המרכז שלו. על פי כלל המקבילית לחיבור ווקטורי של מהירויות, נקבל שכאשר הטרוכואיד מכווץ הנקודה הקבועה נעה תמיד באותו כיוון אופקי (שכן המהירות האופקית של המרכז עולה על מהירות סיבוב הנקודה הקבועה), ולכן אין לו לולאות. כאשר הטרוכואיד מורחב הנקודה משנה את כיוון תנועתה האופקי בחלקים מסוימים של התנועה כך שיש לו לולאות. במקרה הביניים, כאשר הנקודה נחה על היקף הגלגל, מתקבלת הציקלואידה, שלה יש חודים (cusps) בנקודות בהן P נוגעת ב-L.

מבחינה מעשית טרוכואיד מכווץ מותווה על ידי פדל כאשר מפדלים באופניים לאורך קו ישר.

קישורים חיצוניים

מדיה וקבצים בנושא טרוכואיד בוויקישיתוף