זווית דו-מישור

בגאומטריה, הזווית בין שני מישורים נקראת זווית דו-מישור.

הזווית ${\varphi }_{AB}$ בין שני מישורים A ו-B מוגדרת כזווית בין האנכים של מישורים אלה. בפרט, אם נבחר אנכים באורך וקטור יחידה, נקבל את הנוסחה הבאה לזווית הדו-מישורית:

$\cos {\varphi }_{AB}={\mathbf{𝐧}}_A\cdot {\mathbf{𝐧}}_B$

לחלופין, ניתן להגדיר את זווית הדו-מישור ${\varphi }_{AB}$ כזווית בה יש לסובב את מישור A ביחס לקו החיתוך בין המישורים, כדי שיתלכד עם מישור B. הזווית ההפוכה ${\varphi }_{BA}$ תחזיר אותנו ממישור B למישור A, לכן ${\varphi }_{AB}=-{\varphi }_{BA}$. גם הזווית המשלימה ל- ${\varphi }_{AB}$ מאפשרת הגעה ממישור A ל-B.

הגדרות חלופיות

איור 1: זווית הדו-מישור בין שלושה וקטורים

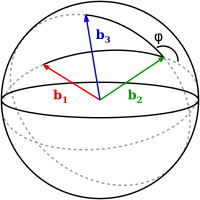
כשם שניתן להגדיר מישור באמצעות שני ישרים הנחתכים בנקודה אחת, ניתן גם להגדיר זווית דו-מישור באמצעות שלושה וקטורים שונים: ${\mathbf{𝐛}}_1$, ${\mathbf{𝐛}}_2$ ו ${\mathbf{𝐛}}_3$ (הווקטורים האדום, הירוק והכחול באיור 1). הווקטורים ${\mathbf{𝐛}}_1$ ו${\mathbf{𝐛}}_2$ מגדירים מישור אחד, בעוד שהווקטורים ${\mathbf{𝐛}}_2$ ו- ${\mathbf{𝐛}}_3$ מגדירים מישור נוסף.

זוויות דו-מישור של ארבעה אטומים

איור 2: זווית הדו-מישור בין שלושה וקטורי קשר כימי, המחברים ארבעה אטומים

בקירוב טוב, קשרים כימיים בין אטומים שכנים במולקולה שומרים על אורכיהם ועל הזוויות היחסיות ביניהם גם כאשר המולקולה מתפרקת למספר מולקולות קטנות יותר, או נקשרת למולקולות אחרות. הודות לכך, ניתן להגדיר את מבנה המולקולה באמצעות סדרה של זוויות דו-מישוריות, שכל אחת מהן מוגדרת על ידי שלישיית וקטורי קשר כימי. כפי שמודגם באיור 2, הזווית הדו-מישורית $\varphi$ משנה רק את המרחק בין האטום הראשון והרביעי. שאר המרחקים הבין-אטומיים באיור מאולצים על ידי אורכי הקשרים הכימיים וזוויותיהם.

איור 3: זווית הדו-מישור בין שלושה וקטורי קשר כימי, המחברים ארבעה אטומים. מנקודת מבט זו, וקטור הקשר השני (הירוק) יוצא מתוך הדף

איור 3 ממחיש את הזווית הדו-מישורית בין ארבעה אטומים. האטום הראשון פונה כלפי מטה, האטום הרביעי פונה באלכסון ימינה ואילו האטומים השני והשלישי ממוקמים במרכז. וקטור הקשר השני יוצא מתוך הדף. הזווית הדו-מישורית $\varphi$ היא הזווית הנוצרת בין הווקטור האדום ${\mathbf{𝐛}}_1$ לבין הווקטור הכחול ${\mathbf{𝐛}}_3$ במגמה מתימטית חיובית (נגד כיוון השעון). כאשר האטום הרביעי משלים הקפה סביב האטום הראשון, הזווית הדו-מישורית מתאפסת. כאשר האטומים הראשון והרביעי נגדיים זה לזה, כמו באיור 2, הזווית הדו-מישורית היא $180^{\circ }$.

זוויות דו-מישוריות במולקולות ביולוגיות

חלבונים בנויים משרשרת של חומצות אמינו המחוברות זו לזו באמצעות קשר פפטידי. נקבעו שמות תקניים לזוויות הדו-מישוריות לאורך השרשרת:

• $\varphi$ עבור האטומים ${\mathrm{C}}^{\mathrm{\prime }}\mathrm{-}\mathrm{N}\mathrm{-}{\mathrm{C}}^{\mathrm{\alpha }}\mathrm{-}{\mathrm{C}}^{\mathrm{\prime }}$
• $\psi$ עבור האטומים $\mathrm{N}\mathrm{-}{\mathrm{C}}^{\mathrm{\alpha }}\mathrm{-}{\mathrm{C}}^{\mathrm{\prime }}\mathrm{-}\mathrm{N}$
• $\omega$ עבור האטומים ${\mathrm{C}}^{\mathrm{\alpha }}\mathrm{-}{\mathrm{C}}^{\mathrm{\prime }}\mathrm{-}\mathrm{N}\mathrm{-}{\mathrm{C}}^{\mathrm{\alpha }}$

כלומר, הזווית $\varphi$ קובעת את המרחק בין אטומי הפחמן של קבוצות הקרבוקסיל של חומצות אמינו שכנות ${\mathrm{C}}^{\mathrm{\prime }}\mathrm{-}{\mathrm{C}}^{\mathrm{\prime }}$. הזווית $\psi$ קובעת את המרחק בין אטומי החנקן של קבוצות האמין של חומצות אמינו שכנות $\mathrm{N}\mathrm{-}\mathrm{N}$. לבסוף, הזווית $\omega$ קובעת את המרחק בין אטומי הפחמן הראשיים של חומצות אמינו שכנות ${\mathrm{C}}^{\mathrm{\alpha }}\mathrm{-}{\mathrm{C}}^{\mathrm{\alpha }}$.

מישוריות הקשר הפפטידי מאלצת את הזווית השלישית $\omega$ להיות $0^{\circ }$ או $180^{\circ }$. התצורה בה$\omega =0^{\circ }$ מכונה תצורת ציס (cis) ואילו התצורה בה $\omega =180^{\circ }$ מכונה תצורת טראנס (trans). אלה תצורות איזומריות. המרחקים בין אטומי הפחמן המרכזיים ${\mathrm{C}}^{\mathrm{\alpha }}$ בתצורות ציס וטראנס הינם בקירוב 2.8 ו-3.8 אנגסטרם, בהתאמה. באופן כללי, תצורת טראנס שכיחה יותר בחלבונים. תצורת ציס מופיעה בעיקר בקשר הפפטידי לקבוצה האימינית של חומצת האימינו פרולין (ראו גם - איזומריות ציס-טראנס).

הזוויות הדו-מישוריות בחלבונים מסומנות כ-${\chi }_1$-${\chi }_5$, בהתאם למרחקן מאטום הפחמן המרכזי הנושא את השייר של חומצת האמינו. הזווית הראשונה ${\chi }_1$ מוגדרת על ידי האטומים $\mathrm{N}\mathrm{-}{\mathrm{C}}^{\mathrm{\alpha }}\mathrm{-}{\mathrm{C}}^{\mathrm{\beta }}\mathrm{-}{\mathrm{C}}^{\mathrm{\gamma }}$, הזווית השנייה ${\chi }_2$ מוגדרת על ידי האטומים ${\mathrm{C}}^{\mathrm{\alpha }}\mathrm{-}{\mathrm{C}}^{\mathrm{\beta }}\mathrm{-}{\mathrm{C}}^{\mathrm{\gamma }}\mathrm{-}{\mathrm{C}}^{\mathrm{\delta }}$, וכן הלאה.

הזוויות הדו-מישוריות בחלבונים נוטות להצטבר בקרבת הזוויות $180^{\circ }$, $60^{\circ }$ ו- $-60^{\circ }$. קיימת השפעה הדדית בין זוויות דו-מישוריות שכנות: רק לעיתים רחוקות נמצא שתי זוויות דו-מישוריות שכנות בגודל $60^{\circ }$ וכו'.

IUPAC הגדירו שמות תקניים גם לזוויות דו-מישוריות במולקולות אחרות, כגון חומצות הגרעין DNA ו-RNA ורב-סוכרים.

ראו גם

• דיאגרמת ראמהצ'אנדרן

קישורים חיצוניים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

זווית_דו-מישור17565458Q911907