התפלגות דיריכלה

התפלגות דיריכלה

פונקציית צפיפות ההסתברות
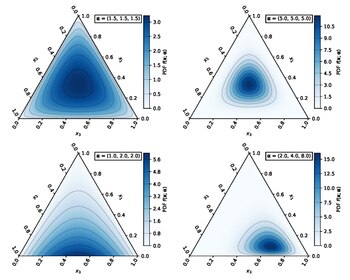מאפיינים
פרמטרים	$K\ge 2$ מספר הקטגוריות (מספר שלם) $\mathit{\alpha }=({\alpha }_1,\dots ,{\alpha }_K)$ הם פרמטרים של ריכוז, כאשר ${\alpha }_i>0$
תומך	$x_1,\dots ,x_K$ כאשר $x_i\in [0,1]$ ו- $\sum _{i=1}^K{x}_i=1$
פונקציית צפיפות הסתברות (pdf)	$\frac{1}{\mathrm{B}(\mathit{\alpha })}\prod _{i=1}^K{x}_i^{{\alpha }_i-1}$ כאשר $\mathrm{B}(\mathit{\alpha })=\frac{\prod _{i=1}^K\mathrm{\Gamma }({\alpha }_i)}{\mathrm{\Gamma }\left({\alpha }_0\right)}$ ו- ${\alpha }_0=\sum _{i=1}^K{\alpha }_i$
תוחלת	$\mathrm{E}[X_i]=\frac{{\alpha }_i}{{\alpha }_0}$ $\mathrm{E}[\ln X_i]=\psi ({\alpha }_i)-\psi ({\alpha }_0)$ (כאשר $\psi$ היא פונקציית דיגמא)
ערך שכיח	$x_i=\frac{{\alpha }_i-1}{{\alpha }_0-K},{\alpha }_i>1.$
שונות	$\mathrm{Var}[X_i]=\frac{{\tilde{\alpha }}_i(1-{\tilde{\alpha }}_i)}{{\alpha }_0+1},$ $\mathrm{Cov}[X_i,X_j]=\frac{{\delta }_{ij}{\tilde{\alpha }}_i-{\tilde{\alpha }}_i{\tilde{\alpha }}_j}{{\alpha }_0+1}$ כאשר ${\tilde{\alpha }}_i=\frac{{\alpha }_i}{{\alpha }_0}$, ו- ${\delta }_{ij}$ היא הדלתא של קרונקר
אנטרופיה	$H(X)=\log \mathrm{B}(\mathit{\alpha })$$+({\alpha }_0-K)\psi ({\alpha }_0)-$$\sum _{j=1}^K({\alpha }_j-1)\psi ({\alpha }_j)$ כאשר ${\alpha }_0$ מוגדר כמו בשונות, למעלה; ו- $\psi$ היא פונקציית דיגמא
פונקציה יוצרת מומנטים (mgf)	${\alpha }_i=E[X_i](\frac{E[X_j](1-E[X_j])}{V[X_j]}-1)$ כאשר $j$ יכול להיות כל אינדקס כולל, $i$ עצמו

בתורת ההסתברות ובסטטיסטיקה, התפלגות דיריכלה (על שם Peter Gustav Lejeune Dirichlet ), מסומנת לעיתים קרובות $\mathrm{Dir}(\mathit{\alpha })$, היא משפחה של התפלגויות רב-משתניות רציפות המוגדרות על ידי וקטור $\mathit{\alpha }$ של ממשיים חיוביים. זוהי הכללה רב-משתנית של התפלגות ביתא, ומכאן שמה החלופי - התפלגות בטא רב-משתנית (MBD). התפלגות דיריכלה משמשת בדרך כלל כהתפלגות פריורית בסטטיסטיקה בייסיאנית, ולמעשה, התפלגות דיריכלה היא ההתפלגות הצמודה של ההתפלגות הקטגוריאלית וההתפלגות המולטינומית.

ההכללה האינסוף-ממדית של התפלגות דיריכלה היא תהליך דיריכלה.

הגדרות

פונקציית צפיפות הסתברות

הדגמה כיצד הלוג של פונקציית הצפיפות משתנה כאשר K = 3 ואנו משנים את הווקטור α מ- α = (0.3, 0.3, 0.3) עד (2.0, 2.0, 2.0), תוך שמירה על כך שכל הרכיבים של $\alpha$ נשארים שווים זה לזה.

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

להתפלגות דיריכלה מסדר $K\ge 2$ עם פרמטרים $0<{\alpha }_1,...{\alpha }_K$, יש פונקציית צפיפות, לפי למידת לבג במרחב האוקלידי ${\mathbb{ℝ}}^{K-1}$, המתוארת באמצעות:

$f(x_1,\dots ,x_K;{\alpha }_1,\dots ,{\alpha }_K)=\frac{1}{\mathrm{B}(\mathit{\alpha })}\prod _{i=1}^K{x}_i^{{\alpha }_i-1}$

כאשר $\{x_k{\}}_{k=1}^{k=K}$ שייכים לסימפלקס $K-1$ תקני, או באופן שקול, לכל $i\in \{1,\dots ,K\}$, ${\sum }_{i=1}^K{x}_i=1\text{, }{x}_i\in [0,1]$.

הקבוע המנרמל הוא פונקציית בטא רב-משתנית, שניתן לבטאו במונחים של פונקציית גמא:

$\mathrm{B}(\mathit{\alpha })=\frac{\prod _{i=1}^K\mathrm{\Gamma }({\alpha }_i)}{\mathrm{\Gamma }\left(\sum _{i=1}^K{\alpha }_i\right)},\mathit{\alpha }=({\alpha }_1,\dots ,{\alpha }_K)$

תומך

התומך של התפלגות דיריכלה היא קבוצת וקטורים $K$ ממדיים $\mathit{x}$ שהערכים שלהם הם מספרים ממשיים בקטע [0,1] כך ש $\Vert \mathit{x}{\Vert }_1={\mathrm{\Sigma }}_i{x}_i=1$, כלומר סכום הקואורדינטות שווה ל-1. למשל עבור $K=3$ התומך הוא משולש שווה-צלעות המשוכן במרחב התלת-ממדי, שקודקודיו בנקודות (1,0,0), (0,1,0) ו (0,0,1), כלומר נמצאים על צירי הקואורדינטות במרחק 1 מהראשית.

תכונות

מומנטים מסדר שני

יהי $X=(X_1,\dots ,X_K)\sim \mathrm{Dir}(\mathit{\alpha })$. ויהי

${\alpha }_0=\sum _{i=1}^K{\alpha }_i$ .

אזי על פי

$\mathrm{E}[X_i]=\frac{{\alpha }_i}{{\alpha }_0},$

$\mathrm{Var}[X_i]=\frac{{\alpha }_i({\alpha }_0-{\alpha }_i)}{{\alpha }_0^2({\alpha }_0+1)}.$

פרט לכך, אם $i\ne j$ אז

$\mathrm{Cov}[X_i,X_j]=\frac{-{\alpha }_i{\alpha }_j}{{\alpha }_0^2({\alpha }_0+1)}$ .

מטריצת הקוויראנס היא אם כך סימטרית והפיכה.

שכיח

השכיח של ההתפלגות הוא הווקטור $(x_1,\dots ,x_k)$ כאשר

$x_i=\frac{{\alpha }_i-1}{{\alpha }_0-K},{\alpha }_i>1$ .

התפלגות שולית

ההתפלגות השוליות הן התפלגויות בטא

$X_i\sim \mathrm{Beta}({\alpha }_i,{\alpha }_0-{\alpha }_i)$ .

קישורים חיצוניים

מדיה וקבצים בנושא התפלגות דיריכלה בוויקישיתוף

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

התפלגות דיריכלה42139002Q981016