השורש הריבועי של 3

השורש הריבועי של 3, אשר מסומן כ-${\sqrt {3}}$ או 3^1/2, הוא המספר הממשי החיובי שכאשר יוכפל בעצמו, תהיה התוצאה שווה ל-3. השורש הריבועי של 3 הוא מספר אי רציונלי. הוא ידוע גם בתור הקבוע של תיאודורוס, על שם תיאודורוס מקירנה, שהוכיח את האי-רציונליות שלו.

נכון לדצמבר 2013, חושבו 10 מיליארד ספרות של ${\sqrt {3}}$. 65 הספרות הראשונות של ${\sqrt {3}}$:

1.73205 08075 68877 29352 74463 41505 87236 69428 05253 81038 06280 55806

הספרות של ${\sqrt {3}}$ הן סדרה A002194 באתר OEIS – האנציקלופדיה המקוונת לסדרות של מספרים שלמים.

השבר9756 (1.732142857...) הוא קירוב לשורש - הוא שונה מהערך הנכון בפחות מ-110,000 (בערך$9.2\times 10^{-5}$).

השבר 716035413403 (1.732 050 807 56...) הוא מדויק בכ-1100000000000 (${\frac {1}{10^{11}}}$).

ארכימדס חישב טווח עבור הערך של השורש: $\left({\frac {1351}{780}}\right)^{2}>3>\left({\frac {265}{153}}\right)^{2}$; הגבול התחתון מדויק עבור 1608400 (6 ספרות אחרי הנקודה) והגבול העליון עבור 223409 (4 ספרות אחרי הנקודה).

ביטויים

ניתן לבטא אותו כשבר משולב [1; 1, 2, 1, 2, 1, 2, 1, …] (סדרה A040001 באתר OEIS – האנציקלופדיה המקוונת לסדרות של מספרים שלמים).

ולכן ניתן לומר כי:

${\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}$

וכאשר $n\to \infty$:

${\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1$

ניתן לבטא אותו גם כשבר משולב מוכלל כגון:

$[2;-4,-4,-4,...]=2-{\cfrac {1}{4-{\cfrac {1}{4-{\cfrac {1}{4-\ddots }}}}}}$

גיאומטריה וטריגונומטריה

הגובה של משולש שווה-צלעות בעל אורכי צלעות 2 הוא ${\sqrt {3}}$. בנוסף, אורך הניצב הארוך במשולש זהב (משולש בעל זוויות 30, 60 ו-90) שאורך היתר שלו הוא 2 הוא ${\sqrt {3}}$.

יתר על כן, הגובה במשושה משוכלל שאורכי צלעותיו הוא 1 הוא ${\sqrt {3}}$.

אורך האלכסון בקוביית יחידה הוא ${\sqrt {3}}$

היטל זה של תריסריון בילינסקי הוא מעוין עם יחס אלכסוני של ${\sqrt {3}}$.

וסיקה פיסקיס

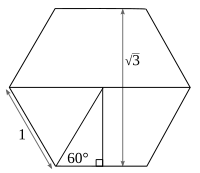
ניתן למצוא את השורש הריבועי של 3 כאורך הצלעות של משולש שווה-צלעות החוסם מעגל בקוטר 1.

אם משולש שווה-צלעות בעל צלעות באורך 1 נחתך לשני חצאים שווים, על ידי חציית זווית פנימית כדי ליצור זווית ישרה עם הצלע שמולה, היתר של המשולש ישר-הזווית הוא באורך 1 ואורכן של הצלעות הוא ${\frac {1}{2}}$ ו-${\frac {\sqrt {3}}{2}}$. מכאן, טנגנס של 60° שווה ל-${\sqrt {3}}$, והסינוס של 60° והקוסינוס של 30° שווים ל-${\frac {\sqrt {3}}{2}}$.

השורש הריבועי של 3 מופיע גם בביטויים אלגבריים עבור קבועים טריגונומטריים אחרים, כולל הסינוסים של 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84° ו-87°.

${\sqrt {3}}$ הוא המרחק בין צלעות מקבילות של משושה משוכלל בעל צלעות באורך 1.

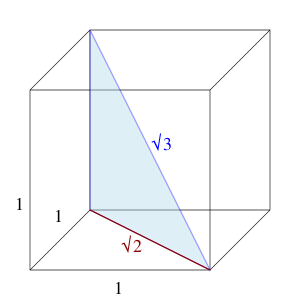
זהו אורך האלכסון הפנימי של קוביית יחידה.

לווסיקה פיסקיס יש יחס בין הציר העיקרי לציר הקטן השווה ל-${\sqrt {3}}$:1. ניתן להראות זאת על ידי בניית שני משולשים שווי-צלעות בתוכו.

שימושים אחרים

הנדסת הספק

בהנדסת הספק, המתח בין שתי פאזות במערכת תלת-פאזית הוא פי ${\sqrt {3}}$ מהמתח לקו הנייטרלי. הסיבה לכך היא שכל שתי פאזות נמצאות במרחק של 120° זה מזה, ושתי נקודות במעגל המרוחקות 120 מעלות זו מזו מופרדות במרחק שגדול פי ${\sqrt {3}}$ מהרדיוס.

ראו גם

• השורש הריבועי של 2

קישורים חיצוניים

מדיה וקבצים בנושא השורש הריבועי של 3 בוויקישיתוף

• הקבוע של תיאודורוס ב-MathWorld

• S., D.; Jones, M. F. (1968). "22900D approximations to the square roots of the primes less than 100". Mathematics of Computation. 22 (101): 234–235. doi:10.2307/2004806. JSTOR 2004806.
• Uhler, H. S. (1951). "Approximations exceeding 1300 decimals for ${\sqrt {3}}$, ${\frac {1}{\sqrt {3}}}$, $\sin({\frac {\pi }{3}})$ and distribution of digits in them". Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443–447. doi:10.1073/pnas.37.7.443. PMC 1063398. PMID 16578382.
• Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers (Revised ed.). London: Penguin Group. p. 23.
• Archimedes and the Square Root of 3
• Department of Mathematics | King’s College London

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

השורש הריבועי של 333810739Q1150815