דיאגרמת פאזות

תרשים פאזות (או דיאגרמת פאזות) הוא תרשים המשמש להצגת פאזות שונות של חומר המתקיימות בשיווי משקל כתלות בפרמטרים תרמודינמיים. כל פאזה בדיאגרמה היא מצב מיקרוסקופי שונה של החומר, ללא שינוי של הרכיבים, המתבטא בתכונות מאקרוסקופיות תרמודינמיות אחידות של החומר.
דיאגרמת פאזות נגזרת מהשינוי באנרגיה החופשית המאפיינת כל מצב כתלות בפרמטר התרמודינמי המתאים.
התרשימים המגדירים דיאגרמת פאזות הם הפרמטרים התרמודינמיים שמשתנים במעבר בין הפאזות השונות כגון: טמפרטורה, לחץ, נפח, ריכוז. דיאגרמת פאזות יכולה לתאר פאזות של חומר אחיד או של תערובת של חומרים כתלות בריכוז של כל אחד מהמרכיבים.
מאפיינים של דיאגרמת פאזות
דיאגרמת פאזות באופן כללי מוצגת כתלות בפרמטרים תרמודינמיים המהווים את הצירי הדיאגרמה. בנוסף, ישנם מספר מאפיינים המוצגים ומסומנים בדיאגרמה. דיאגרמת פאזות יכולה לכלול קווי דו קיום של שתי פאזות, נקודות מפגש של מספר פאזות (כמו נקודה משולשת למשל בדיאגרמת פאזות של מים, איור (1)), נקודות קריטיות, טמפרטורות התכה ועוד סימונים ייחודיים בהתאם לחומר המתואר.
קווי דו-קיום
קווי דו-קיום הם קווים המייצגים תנאים תרמודינמיים מסוימים אשר לאורכם מתקיימות שתי פאזות במקביל בשיווי משקל, מיקום הקווים כתלות בפרמטרים התרמודינמיים נגזר מאי רציפות בנגזרת של האנרגיה החופשית, כלומר הערכים התרמודינמיים שבהם מתרחש המעבר בין שתי הפאזות שמצידי קו הדו-קיום.
נקודה משולשת
 ערך מורחב – נקודה משולשת
ערך מורחב – נקודה משולשת
נקודה משולשת היא נקודה המציינת את התנאים התרמודינמיים לקיומן של 3 פאזות במקביל בשיווי משקל. למשל בדיאגרמת פאזות של מים כתלות בלחץ ובטמפרטורה, קיימת נקודה אחת של טמפרטורה ולחץ שבה מתקיימות שלוש הפאזות בשיווי משקל: מים, קרח ואדים.
ניתן לחשב מראש עבור דיאגרמה של חומר מסוים את מספר הפאזות שניתן לקבל בנקודה מסוימת או לאורך קו בשיווי משקל בהתאם לחוק הפאזות של גיבס.
נקודה קריטית
 ערך מורחב – נקודה קריטית
ערך מורחב – נקודה קריטית
נקודה קריטית היא נקודה המציינת את הערכים של הפרמטרים התרמודינמיים אשר מן העבר האחד שלהם קיימת הפרדה לפאזות שונות בשיווי משקל ומן העבר השני אין הפרדה בין פאזות. בנקודה זו הערכים התרמודינמיים הם כאלו שבהם מתרחש המעבר מאנרגיה חופשית בעלת שתי נקודות מינימום כתלות בפרמטר התרמודינמי המתאר את המערכת, לאנרגיה חופשית עם נקודת מינימום אחת. המערכת שואפת להימצא במינימום של האנרגיה החופשית תיפרד לשתי פאזות במקרה שבו יש לה שתי נקודות מינימום ותהיה בעלת פאזה אחת בלבד בשיווי משקל במקרה של מינימום יחיד, הנקודה הקריטית מתארת את המעבר הזה (דוגמה לגזירת דיאגרמת פאזות מתוך האנרגיה החופשית נמצאת בהמשך הערך). למשל בדיאגרמת פאזות של מים – הנקודה הקריטית מציינת את הלחץ והטמפרטורה אשר מהם והלאה לא מתקיימות שתי פאזות נפרדות של נוזל וגז אלא פאזה אחת המכונה "זורם" .[1]
סוגים של דיאגרמת פאזות
דיאגרמת פאזות דו ממדית
דיאגרמת הפאזות הפשוטה ביותר היא דיאגרמה של טמפרטורה ולחץ עבור חומר אחד כמו למשל מים (איורים 1, 6). הצירים בדיאגרמה הם הטמפרטורה והלחץ, הדיאגרמה מציגה במרחב הטמפרטורה והלחץ את קווי הדו-קיום שמפרידים בין הפאזות השונות של המים: מוצק, נוזל וגז. הנקודה המשולשת מציגה את התנאים לקיום שלוש הפאזות בו זמנית בשיווי משקל והנקודה הקריטית מציגה את התנאים של הלחץ והטמפרטורה אשר מעליהם אין הבדל בין נוזל לגז ומתקיימת פאזה אחת – זורם.
האזורים הפתוחים בדיאגרמה מייצגים אזורים בהם האנרגיה החופשית אנליטית ומתקיימת רק פאזה אחת בשיווי משקל. אזורים אלו מופרדים על ידי קווי הדו-קיום בהם האנרגיה החפשית לא אנליטית ודרכם מתרחש תהליך מעבר פאזה, אלו הם גבולות הפאזה.
תכונות תרמודינמיות נוספות
מלבד טמפרטורה ולחץ, ישנם פרמטרים תרמודינמיים נוספים שיכולים להופיע בדיאגרמת פאזות כגון נפח סגולי, אנתלפיה סגולית או אנטרופיה סגולית כמוצג באיור (2). לדוגמה: דיאגרמת פאזות של חומר אחד בה מופיעה הטמפרטורה כפונקציה של האנטרופיה הסגולית עבור מים/אדים או נוזל קירור, משמשים להדגמת מעגלים תרמודינמיים כמו מעגל קרנו, מעגל רנקין.
 |
 |
 |
| איור 2 (א) - דיאגרמה של אנתלפיה - אנטרופיה (S-H) עבור אדים | איור 2 (ב) - דיאגרמה של לחץ - אנתלפיה (p-H) עבור אדים | איור 2 (ג) - דיאגרמה של טמפרטורה - אנטרופיה (S-T) עבור אדים |
קווים שווי ערך
בגרף דו ממדי, שני פרמטרים תרמודינמיים יכולים להוות את שני הצירים – האופקי והאנכי. בנוסף ניתן לצייר גדלים תרמודינמיים אחרים בצורה של סדרת קווים עוקבים כך שכל קו מסמן ערך אחד קבוע של אותו גודל תרמודינמי. הקווים יכולים להיות ישרים או עקומים כתלות בתנאים התרמודינמיים של החומר. למשל בדיאגרמה שבה הצירים הם לחץ ונפח ניתן לצייר קווים שווי טמפרטורה המכונים איזותרמות כמו בדיאגרמה של גז ואן דר ואלס או קווים שווי-לחץ בדיאגרמה של טמפרטורה מול אנטרופיה כמוצג באיורים (2) (3).

דיאגרמת פאזות תלת ממדית
דיאגרמת פאזות תלת ממדית
אפשר להציג דיאגרמת פאזות כתלות בשלושה פרמטרים תרמודינמיים.[2][3] לדוגמה עבור חומר אחד, ניתן להציג במערכת קרטזית של 3 צירים: טמפרטורה T, לחץ p ונפח סגולי v, לעיתים גרף זה נקרא דיאגרמת p-v-T, תיאור סכימתי מוצג באיורים (4,5). תנאי שיווי משקל מוצגים כעקומות על גבי משטח עקום בתלת מימד, עם אזורים עבור מוצק, נוזל וגז, ואזורי דו קיום של שתי פאזות: נוזל וגז, נוזל ומוצק, מוצק וגז. בדיאגרמה זו ישנו קו "משולש" שבו מתקיימות שלוש הפאזות בו זמנית בשיווי משקל. הנקודה הקריטית בדיאגרמה התלת ממדית נשארת נקודה אחת, כלומר ערך אחד של כל פרמטר אשר במשולב מהווים את הנקודה הקריטית.
ההיטלים של דיאגרמה תלת ממדית p-v-T, יוצרים תרשימים דו ממדיים אשר מציגים את קווי הדו קיום של כל שתי פאזות שהם ההיטל של מישורי דו קיום מהדיאגרמה התלת ממדית.
 |
 |
דיאגרמת פאזות לפי מספר רכיבים
דיאגרמת פאזות של חומר המורכב מרכיב אחד

דיאגרמת פאזות דו-ממדית טיפוסית של רכיב אחד (חומר המורכב מסוג אחד של מולקולה, כמו למשל מים) מוצגת באיור (6). ניתן לראות שהדיאגרמה מקיימת את חוק הפאזות של גיבס כך שקיימים אזורים של פאזה אחת עם שתי דרגות חופש (לחץ וטמפרטורה), קווי דו-קיום שמאפשרים דרגת חופש אחת, לדוגמה בהינתן ערך מסוים של הלחץ, עקום הדו-קיום יקבע את הטמפרטורה. כמו כן קיימת נקודה משולשת אחת שבה מתקיימות שלוש פאזות בשיווי משקל. לפי חוק הפאזות של גיבס מתקבל כי אין מפגש של יותר משלוש פאזות בשיווי משקל עבור דיאגרמה של חומר מרכיב אחד.
מרחב p-T מחולק לשלושה אזורים, כאשר בכל אחד החומר יציב כמו בחומר עם מצב צבירה אחד. העקומות המפרידות בין האזורים מתארות דו קיום של שתי פאזות ומקיימות את משוואת קלאוזיוס-קלפרון.
כל עקומה משלוש העקומות באיור (6) מתארת את האזור במרחב הלחץ-טמפרטורה שבו שתי פאזות נמצאות בשיווי משקל ומתקיים שוויון של האנרגיה החופשית של שתי הפאזות. בנקודת החיתוך של שלוש העקומות מתקיים ששלוש האנרגיות החופשיות של שלוש הפאזות שוות זו לזו. יש ערך אחד של לחץ וערך אחד של טמפרטורה – הנקודה המשולשת שמאפשר קיום שלוש הפאזות בשיווי משקל בו זמנית.
קו הדו קיום בין נוזל למוצק ברוב החומרים הוא בעל שיפוע חיובי, כלומר ככל שעולה הלחץ, כך המולקולות של החומר מתקרבות זו לזו וכתוצאה מכך מתחזקים הכוחות הבינמולקולריים בחומר. לכן נדרשת טמפרטורה גבוהה יותר על מנת לאפשר למולקולות לצאת מהמצב הקשור במוצק ולעבור למצב נוזלי בחומר. מצב דומה מתרחש במעבר מנוזל לגז. למים תכונות אנומליות ולכן הדיאגרמה עבור מים מתנהגת שונה מבחינת הנקודות הקריטיות והשיפוע של קו דו הקיום בין הנוזל למוצק כפי שניתן לראות באיור (6) בקו הירוק המקוטע לעומת חומרים אחרים המצייתים לקו הירוק הרציף.
עבור מערכת של חומר אחד יכול להתקיים:
- פאזה אחת של: גביש מוצק, נוזל גבישי לא-איזוטרופי, נוזל איזוטרופי או אדים.
- שתי פאזות: מוצק/נוזל כמו למשל קרח נמס, נוזל/גז כמו למשל בנזן רותח, מוצק/גז כמו למשל פחמן דו-חמצני במצב של המראה – קרח יבש.
- שלוש פאזות: מוצק, נוזל וגז כמו מים; מוצק א', מוצק ב' וגז כמו גופרית בתנאי לחץ של וטמפרטורה ℃ 95.6 ; נוזל אנאיזוטרופי, נוזל איזוטרופי וגז כמו למשל חומצה מתוקסיצינמית (נמצאת בקרם הגנה מהשמש) בתנאי לחץ של bar 0.06 וטמפרטורה ℃ 185.
חלק ניכר מהמוצקים הנמצאים תחת לחץ אטמוספירי, מותכים לנוזל בחימום, כלומר, הנקודה המשולשת שבה מוצק, נוזל וגז מתקיימים בשיווי משקל בו זמנית מתרחשת בלחץ נמוך מ-1 bar. אולם לחומרים מסוימים יש נקודה משולשת בלחץ גבוה מ-1 bar (לדוגמה )
ולכן ממריאים (עוברים ללא התכה ישירות ממוצק לגז) כאשר מחממים אותם תחת לחץ אטמוספירי. תחת לחץ גבוה גבוה משל הנקודה המשולשת הם יכולים כמובן לעבור התכה למצב נוזל בחימום.
דיאגרמת פאזות בינארית - שני רכיבים
דיאגרמת פאזות של חומרים בינאריים, כלומר חומרים המורכבים משני חומרי בסיס כמו סגסוגות. הדיאגרמה מיוצגת לרוב על ידי ציר של החלק היחסי של שני הרכיבים בתערובת למול ציר הטמפרטורה עליו מסומנות טמפרטורות מעבר הפאזה של שני החומרים. תערובת כזו יכולה להיות בין היתר תערובת מוצקה, תערובת אוטקטית או פריטקטית. כל סוג של תערובת בינארית ייצור דיאגרמה שונה.[4]
עבור מערכת בינארית, חוק הפאזות מקיים f=4-P, כאשר f מספר דרגות החופש ו-P מספר הפאזות, ומאפשר קיומן של עד 4 פאזות בשיווי משקל.
ניתן להציג ביותר משני ממדים דיאגרמה של פאזות החומר כתלות ב-3 פרמטרים תרמודינמיים שונים. מלבד לחץ, טמפרטורה וריכוז, ניתן להשתמש בפרמטרים אחרים כמו למשל הכוח של הפעלת שדה חשמלי או מגנטי על החומר, כמו כן ניתן להציג יותר מ-3 פאזות שונות של אותו חומר.
דיאגרמת פאזות של שני רכיבים בעלי מסיסות מלאה

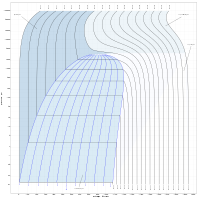
"דיאגרמת סיגר" דיאגרמה המציגה את הפאזות של שני חומרים המקיימים מסיסות מוחלטת אחד בשני. כמוצג באיור (7), הדיאגרמה הדו ממדית מוצגת לפי ציר הריכוז היחסי של כל אחד מהחומרים המרכיבים את התערובת, כפונקציה של הטמפרטורה. האזור הוורוד הוא אזור שבו מתקיימת פאזה אחת A (למשל נוזלית) של שני החומרים ביחד, האזור הכחול הוא אזור שבו מתקיימת פאזה B (למשל מוצקה) של שני החומרים ביחד, האזור הירוק תחום על ידי שני עקומים הנחתכים בשתי נקודות מעבר הפאזה של שני הרכיבים, בו כל נקודה בו מתפצלת לשתי נקודות על העקומים העליון והתחתון ולפי הערך המתאים על העקום נקבע איזו כמות מהחומר תהיה במצב צבירה A או B ומה הריכוז היחסי של כל אחד מהרכיבים בכל אחת מהפאזות. למשל עבור האיזותרמה המסומנת באדום נקבל לפי החיתוך עם העקומים את ההפרדה בין שתי הפאזות ואת הריכוז של החומר (כמה מרכיב 1 וכמה מרכיב 2) בכל אחת מהפאזות A ו-B.
ניתן לחשב את החלק היחסי של החומר בכל אחת מהפאזות לפי המשוואה הבאה:
כאשר החלק היחסי של החומר הכולל בפאזה A, ו- הריכוז ההתחלתי של רכיב 1 בחומר,
הריכוז של רכיב 1 בפאזה A, ו- הריכוז של רכיב 1 בפאזה B.
החלק היחסי של החומר הכולל בפאזה B יהיה פשוט החלק המשלים, כלומר:
.
התנאים לקיום מסיסות מוחלטת שתאפשר תיאור באמצעות דיאגרמת פאזות של מסיסות מוחלטת בין שני חומרים:
המבנה הסריגי של שני החומרים צריך להיות זהה, גודל המולקולות של שני החומרים צריך להיות דומה, טמפרטורות ההתכה של שני החומרים צריכות להיות קרובות.
באיור (7) מוצגת דוגמה היפותטית לדיאגרמת פאזות של תערובת שני חומרים 1 ו-2 שאינם אזיאוטרופים כפונקציה של הריכוז היחסי שלהם בתערובת.
האיור יכול לתאר מעבר ממוצק (פאזה B) לנוזל (פאזה A), במקרה זה העקום העליון התוחם את האזור הירוק יהיה "ליקווידוס" והעקום התחתון יהיה "סולידוס".[5] כמו כן האיור יכול לתאר מעבר מנוזל לגז,
דוגמה לדיאגרמת מסיסות מלאה של תערובת בינארית היא דיאגרמת נקודת הרתיחה עבור תרכובת כימית של שני חומרים.
עבור שני מרכיבים נדיפים בתנאי לחץ מסוימים כמו לחץ אטמוספירי, דיאגרמת נקודת הרתיחה מציגה אילו רכיבים של אדי החומר נמצאים בשיווי משקל עם הרכב מסוים של הנוזל בתנאי טמפרטורה מסוימים. דיאגרמת פאזות בינארית של נקודת רתיחה מכילה בדרך כלל את הטמפרטורה בציר האנכי ואת הריכוז היחסי בין החומרים בציר האופקי. במקרה כזה התרשים יכלול שתי עקומות נפרדות המחברות את נקודות הרתיחה של שני החומרים במצבם הטהור, מצב זה מעיד על כך שההרכב של תערובת האדים יכול להיות שונה מההרכב של התערובת הנוזלית עימה האדים נמצאים בשיווי משקל.
דיאגרמת פאזות אוטקטית

דיאגרמת פאזות אוטקטית מאפיינת לרוב סגסוגות (למשל Bi-Cd, Sn-Zn, Ag-Cu, Al-Si) ומכונה על שם הטמפרטורה הקריטית הקבועה או איזותרמה שמגדירה את הדיאגרמה. דיאגרמה אוטקטית מתקיימת עבור שני חומרים שאין ביניהם מסיסות מוחלטת, כאשר ההבדל בטמפרטורת ההתכה של שני החומרים לא גדול אבל הסימטריה של המוצקים שונה.
בדיאגרמה הבינארית האוטקטית שני עקומי המסיסות נחתכים בנקודה האוטקטית (מיוונית – קל מסיסות) המסומנת באדום באיור (8) (הדיאגרמה מציגה מצב של לחץ קבוע). הטמפרטורה האוטקטית נמוכה מטמפרטורות ההתכה של שני החומרים הטהורים המרכיבים את התערובת ומתקבלת כאשר האנרגיה החופשית של פאזת הנוזל ופאזות המוצקים שוות.
מעל לטמפרטורה האוטקטית מתקיימת פאזת נוזל משותפת. מתחת לטמפרטורה זו, כל הרכב של שני החומרים יהיה לא יציב כנוזל ותתרחש הפרדת פאזות של שני המוצקים.
הדיאגרמה (איור 8), מוצגת לפי הריכוז היחסי של כל אחד מהחומרים בציר האופקי והטמפרטורה בציר האנכי.
נקודות המצוינות על גבי הגרף: נקודות ההתכה של שני החומרים: עבור הציר השמאלי שבו ריכוז חומר B הוא 100% תצוין נקודת ההתכה של חומר B ובהתאם, בציר הימני שבו מתקיים ריכוז חומר A הוא 100%, תצוין נקודת ההתכה של חומר A.
ההפרדה לשתי פאזות של תערובת מוצקה מתוארת על ידי המשוואה:
.
אם המטרה היא לקבל חומר מעורב, יש תחרות בין קצב הקירור לקצב הפרדת הפאזות ותהליך קבלת התערובת נקרא "Quanching". התהליך מתחיל כאשר החומר במצב ובטמפרטורה של התערובת הנוזלית ואז מתבצע קירור בבת אחת של כל הדגם כך שהחומר לא יספיק להסתדר מחדש ולהיפרד לפאזות שונות כך שנקבע את התערובת שנוצרה כנוזל ונקבל תערובת מוצקה.
סולידוס
היא הטמפרטורה שממנה ולמטה החומר יציב במצב מוצק, מנקודה זו יוצא עקום המתאר את הערך המתאים של ריכוז כל אחד מהרכיבים בטמפרטורה נתונה הנמצאת באזור האזור שבו לא מתקיים חומר.[6]
ליקווידוס
היא הטמפרטורה שממנה ומעלה החומר יציב במצב נוזל.
יכול להיות מצב של פער בין שתי הטמפרטורות הנ"ל, בתחום ביניים זה תיווצר תערובת של גביש ונוזל.
דיאגרמת פאזות פריטקטית

מתקיימת כאשר יש הבדל גדול בין טמפרטורות ההתכה של שני החומרים בתערובת. התגובה הפריטקטית על גבי הדיאגרמה מאופיינת באיזותרמה חשובה (אפס דרגות חופש) ונראית כמו דיאגרמה אוטקטית נוטה למטה.
ניתן לתאר את התהליך על ידי המשוואה:
נקודה פריטקטית בדיאגרמת פאזות היא נקודה שמעליה פאזה B נמסה ונוצרת הפרדת פאזות. הדיאגרמה מתקבלת מהתחרות באנרגיה החופשית בין הפאזה הנוזלית לפאזה המוצקה. ישנם חומרים שמקיימים דיאגרמה פריטקטית בלבד לאורך כל טווח הטמפרטורות כמו למשל הסגסוגת Pt-Re . בניגוד לדיאגרמה האוטקטית, בדיאגרמה הפריטקטית קיים מצב נוזלי גם מתחת לנקודת החיתוך של שני עקומי המסיסות.
שילוב של מערכות אוטקטיות
עבור חומרים בעלי קישור חזק מתקיימת דיאגרמת פאזות מהצורה המוצגת באיור (10). דיאגרמה זו נוצרת משילוב של שתי מערכות אוטקטיות זו לצד זו כמו למשל עבור GaAs בעל החשיבות במוליכים למחצה שילוב של המערכת האוטקטית As-GaAs עם המערכת האוטקטית Ga-GaAs. בדיאגרמה מסוג זה מתקבל קו אחד של פאזה שבה מתקיים רק GaAs (מסומן בקו צהוב באיור 10).


גזירת דיאגרמת פאזות מתוך ערכי האנרגיה החופשית
איור 11 מציג את האנרגיה החופשית כתלות בריכוז היחסי של שני רכיבים המרכיבים חומר מסוים. כל אחד מהאיורים מציג את ההתנהגות של האנרגיה החופשית בטמפרטורה מסוימת כאשר T1>T2>T3>T4. המצב המועדף מבחינה תרמודינמית יהיה זה שנותן מינימום של האנרגיה החופשית בשיווי משקל ולכן עבור הגרף העליון שבו העקום של הנוזל נמצא כולו מתחת לעקום של המוצק, החומר יהיה במצב נוזל. עם הורדת הטמפרטורה העקומים של המוצק והנוזל יתחילו לחתוך זה את זה כך שבאותה טמפרטורה, בריכוזים מסוימים המערכת בשיווי משקל תהיה מוצק ובריכוזים אחרים נוזל. עבור סט של דיאגרמות של האנרגיה החופשית כפונקציה של הריכוז ניתן ליצור דיאגרמת פאזות שתתאר את ההפרדה של החומר לפאזות השונות כתלות בריכוז ובטמפרטורה.
סימולציה של דיאגרמת פאזות
ניתן לבצע סימולציות של מעברי פאזה על ידי קוד מחשב ושימוש במשוואות דיפרנציאליות חלקיות. ניתן לבנות את הקוד לדוגמה לפי שיטת מונטה קרלו או לפי שיטת דינמיקה מולקולרית.[7]
ראו גם
- מעבר פאזה
- מצב צבירה
- חוק הפאזות של גיבס
- תורת לנדאו
- תערובת אוטקטית
- תרמודינמיקה
- נקודה משולשת
- נקודה קריטית
- אנרגיה חופשית
- סגסוגת
- המראה (פיזיקה)
לקריאה נוספת
- Michael P. Marder, Condensed Matter Physics
- Milton Ohring, Engineering Materials Science
- R.Koningsveld, W.H.Stockmayer, E.Nies, Polymer Phase Diagrams
- Mats Hillert, Phase Equilibria Phase Diagrams and Phase Transformations
- E.K Molchanova, Phase Diagram of Titanium Alloys
קישורים חיצוניים
- הסבר על דיאגרמת פאזות אוטקטית (באנגלית) ב-youtube
- דיאגרמת פאזות, באתר של ד"ר דנה אשכנזי
- cbhh בניית דיאגרמת פאזות (באנגלית)
- דוגמה לדיאגרמת פאזות של סגסוגות (באנגלית)
- דיאגרמת פאזות של ברזל (באנגלית)
- מעברי פאזה ודיאגרמות פאזות (באנגלית)
- ספריית דיאגרמות פאזות (באנגלית) באתר אוניברסיטת קיימברידג'
- דיאגרמת פאזות, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים
- ↑ P. Papon, J. Leblond, and P.H.E. Meijer, The Physics of Phase Transition - Concepts and Applications Springer 1999.
- ↑ Heat and Thermodynamics, Mark W. Zemansky, Richard H. Dittman, McGraw-Hill, 6th ed., 1981, Figures 2-3, 2-4, 2-5, 10-10, P10-1, מסת"ב 0-07-072808-9.
- ↑ Web applet: 3D Phase Diagrams for Water, Carbon Dioxide and Ammonia. Described in A. Herráez, R.M. Hanson, and L. Glasser J. Chem. Educ. 86 (5), 566 (May 2009).
- ↑ Milton Ohring, Engineering Materials Science .
- ↑ R.Koningsveld, W.H.Stockmayer, E.Nies, Polymer Phase Diagrams .
- ↑ Predel, Bruno; Hoch, Michael J. R; Pool, Monte. Phase Diagrams and Heterogeneous Equilibria : A Practical Introduction. Springer. ISBN 3-540-14011-5.
- ↑ Michael P. Marder, Condensed Matter Physics .
דיאגרמת פאזות31847605Q186693


