אפנון משרעת

דוגמה של אפנון משרעת (במישור הזמן). התרשים העליון מראה את הגל (באדום) שאותו מעוניינים לאפנן, ואת הגל הנושא (ירוק). התמונה התחתונה מראה את תוצאת אפנון המשרעת בין שני הגלים.

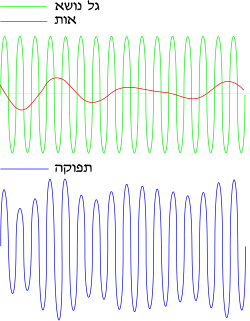
אפנון משרעת או אפנון תנופה (אמפליטודה) (באנגלית: AM; Amplitude Modulation) הוא שיטת שידור לשם העברת מידע המורכב על גבי גלים אלקטרומגנטיים בתדר רדיו כך שמשרעת (עוצמת) הגל המשודר משתנה בתלות במידע, בעוד תדר הגל נשאר ללא שינוי. בדרך כלל תדירות הגל הנושא גבוהה יותר מהתדירות של המידע המורכב עליו. שיטה זו נועדה בעיקר להפצת אותות שמע אלחוטיים, אך ניתן להעביר בה גם צפנים ונתונים. שיטה זו נפוצה בשידורי הרדיו בתחום הגלים הארוכים, הבינוניים והקצרים.

אפנון משרעת מתבצע על ידי הכפלת האות לשידור באות קוסינוס בתדר מסוים (הגל הנושא). במישור התדר האות מכיל שתי אונות צד סימטריות (זהו גל המידע), בתדרים שמעל ומתחת לתדר הגל הנושא. אפנון AM מתבצע במשדר על ידי הכנסת אות השידור והגל הנושא למיקסר RF (ערבל תדר רדיו). במקלט מתבצעת פעולת הגילוי והפענוח של המידע הנקלט, שהיא הפרדת המידע מהגל הנושא אותו. פעולה זו מבוצעת לרוב על ידי יישור הגל (קטימת מחצית הגל המיותרת), לרוב על ידי שימוש בדיודה. פעולת הסינון נעשית לרוב על ידי שימוש בקבל או במערכות מבוססות קבלים.

אפנון AM הוא קל לביצוע, אבל בזבזני ברוחב הסרט מכיוון שנדרש רוחב סרט כפול מרוחב הסרט של האינפורמציה. בין הפתרונות לבעיה זו נמצאים אפנונים "מבוססי" AM, ביניהם DSB ו-SSB. כמו כן, אפנון משרעת רגיש יחסית לרעשים ולהפרעות. בנוסף, אפנון זה בזבזני בהספק, שכן רק חלק קטן מהאנרגיה המשודרת מנוצל להעברת מידע.

תיאור מתמטי של אפנון משרעת

פעולת האפנון מתבצעת, כאמור, עלי ידי שימוש בשני אותות: האות הנושא ואות המידע. נניח כי משוואת הנושא היא

$c(t)=C\cos ({\omega }_{c}t)$

כאשר c מבטא את תנופת האות הנושא ו- ${\omega }_c$ את תדירותו הזוויתית של הגל הנושא (כאשר ${\omega }_c=2\pi f_c$ וכאשר f_c היא תדירות הנושא).

נניח כי $m(t)=M\cos ({\omega }_{m}t+\varphi )$

היא משוואת גל המידע כאשר M היא תנופת המידע ו- ${\omega }_m$ היא תדירותו הזוויתית של גל המידע (כאשר ${\omega }_m=2\pi f_m$ וכאשר f_m היא תדירות גל המידע) כך ש-φ הוא הפרש המופע בין המידע לנושא.

פעולת האפנון מתבצעת על ידי הוספת גל המידע לנושא והכפלת הביטוי ב- $\cos ({\omega }_{c}t)$. התוצאה המתקבלת היא:

$X_{AM}(t)=[C+m(t)]\cos ({\omega }_{c}t)=[C+M\cos ({\omega }_{m}t+\varphi )]\cos ({\omega }_{c}t)$.

על ידי שימוש בנוסחאות טריגנומטריות ניתן להציג נוסחה זו בדרכים נוספות, ביניהן:

$X_{AM}(t)=C\cos ({\omega }_{c}t)+\frac{M}{2}[\cos (\varphi +({\omega }_m+{\omega }_c)t)+\cos (\varphi +({\omega }_m-{\omega }_c)t)]$.

כדי לקבל את האות המקורי יש לבצע פעולת גילוי אשר מסירה את האפנון ומשחזרת האות המקורי. גלאי נפוץ הוא גלאי מעטפת.

עומק אפנון

אחד ממאפייניו החשובים של אות המשודר באפנון משרעת הוא עומק האפנון (נקרא גם "מקדם אפנון" או "יחס אפנון"). עומק האפנון מוגדר כיחס שבין תנופתו המקסימלית של גל המידע לבין תנופתו המקסימלית של הגל הנושא, כלומר:

$m_a=\frac{M}{C}$ כאשר נוהגים להעביר את הצגתו של עומק האפנון לאחוזים.

בהינתן הגדרה זו, ניתן להציג את נוסחת האפנון גם בדרך הבאה:

$X_{AM}(t)=C[1+m_a\cos ({\omega }_{m}t)]\cos ({\omega }_{c}t)$.

ניתן להוכיח כי באופן אידיאלי נצילות שידור AM תלויה בעומק האפנון בלבד ונתונה על ידי הביטוי:

$\eta =\frac{1}{1+\frac{2}{m_a^2}}$.

לפיכך, באופן אידיאלי, אם ברצוננו לשמור על נצילות גבוהה, יש להשתמש בעומק אפנון גבוה ככל הניתן. באופן מעשי, משתמשים בעומק אפנון של כ - 30% עקב מגבלות טכניות בגלאי אפנון משרעת.

ראו גם

• אפנון תדר
• אפנון פאזה
• תדר רדיו
• AM (תחום)

קישורים חיצוניים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

אפנון_משרעת22190176Q183755