אוטומט תאי

אוטומט תאי הוא מודל הנחקר במסגרת תורת החישוביות, מתמטיקה וביולוגיה תאורטית. הוא כולל סריג (או באופן כללי גרף) של תאים, שלכל אחד מהם מספר סופי של מצבים. התא קשור למספר תאים סביבו ומאפיין זה נקרא סביבה. הסביבות הנפוצות הן סביבת מור וסביבת פון נוימן. הזמן במודל הוא בדיד, ומצבו של כל תא בזמן נתון t הוא פונקציה של מצבו ומצב תאים אחרים (שכניו של התא הנתון) בזמן t-1. פונקציה זו חלה על כל התאים, כלומר כל התאים משתנים על-פי אותה מערכת של כללים. כל הפעלה של הפונקציה על כל התאים בסריג יוצרת דור חדש.
המימוש המקובל של אוטומט תאי הוא באמצעות תוכנית מחשב, המפתחת מצב נתון על בסיס של חוקים פשוטים, ועוקבת אחר ההתפתחות לאורך זמן. אוטומטים ראשונים מהסוג הזה נבנו מתוך מחשבה לחקות חיים בעזרת תוכנית מחשב, ובהם כל משבצת על המסך סימנה "תא", ולכן הם זכו לשם אוטומטים תאיים. הדחיפה העיקרית לחקר אוטומטים אלו באה מתוך משחק החיים שפיתח ג'ון קונויי, משחק שזכה להדים רבים בקהילה המדעית ומחוצה לה.
הקדמה ורקע היסטורי
המצאת המחשב המודרני, באמצע המאה ה-20 אפשרה ביצוע סימולציות המדמות תופעות טבע שונות, בפיזיקה, בכימיה ולמעשה לכל רוחב מדעי הטבע. בבנייה של סימולציות, הדגש נמצא לרוב על בנייה של סימולציה הקרובה ככל הניתן למציאות, כך שניתן בעזרתה לקבל תוצאות כמותיות. על שאלות כמותיות רבות ניתן לקבל תשובות טובות בעזרת סימולציות, כגון "האם ירד גשם מחר?", "איפה בדיוק יימצא כדור-הארץ בעוד 10 שנים?" וכדומה. לעומת זאת ישנה גישה הפוכה השואלת: מה המודל הפשוט ביותר שיכול לשחזר התנהגויות הנראות בטבע? במודלים אלו הדגש הוא על שחזור של התנהגויות איכותיות, ולא כמותיות, והרעיון הוא לגלות בעזרתם מהם הגורמים החשובים ביותר המאפשרים את ההתנהגויות הנצפות בטבע. מודלים כאלו נמצאו שימושיים למגוון רחב של תחומים כגון חקר תופעות המדבור, חקר מערכות אבולוציוניות ועוד. מחקרים אלו גם העלו את השאלה הבסיסית של איך מתנהגים האוטומטים התאיים הפשוטים ביותר (מבלי לקשר אותם למערכות הקיימות בטבע).
המצאת האוטומט התאי הראשון מיוחסת למתמטיקאים ג'ון פון נוימן וסטניסלב אולם. פון נוימן, אחד המתמטיקאים החשובים של המאה הידוע בעיקר בזכות יצירת תורת המשחקים, ניסה בשנות ה-40 של המאה ה-20 לבנות רובוטים המסוגלים לשכפל את עצמם. כאשר נתקל בקשיים רבים בפיתוח רעיון זה, הציע לו סטניסלב אולם להשתמש למטרה זו במודל מתמטי אבסטרקטי, של לוח משבצות, בדומה למאמצים שעשה אולם בחקר גדילה של גבישים. פון נוימן אכן הצליח לבנות אוטומט תאי, שבו כל משבצת יכולה להימצא באחד מ-29 מצבים. באוטומט שיצר קיים יצור שעם הזמן יוצר אין סוף עותקים של עצמו.
המדען הראשון להפעיל סימולציה של אוטומט תאי על מחשב היה המתמטיקאי הנורווגי נילס אלס בריצ'לי ( Nils Aall Barricelli) בריצ'לי הוזמן על ידי פון נוימן בשנת 1953 לפרינסטון על מנת לעבוד על מחשב האניאק (אחד המחשבים הראשונים שנבנו, נבנה על ידי פון נוימן כחלק מפרויקט הגרעין האמריקאי במלחמת העולם השנייה). בריצ'לי הריץ תוכנות מחשב המפתחות מצבים פשוטים בחיפוש אחר 'חיים מלאכותיים'.
בשנת 1970 המציא המתמטיקאי ג'ון קונויי את האוטומט התאי המפורסם ביותר, לו קרא משחק החיים. משחק החיים זכה לפופולריות רבה מאוד בקרב מתמטיקאים, מתכנתים וחובבי שעשועי מתמטיקה, במידה רבה בזכות סדרת מאמרים מאת מרטין גרדנר אודותם, שפורסמה בירחון Scientific American. בין השאר התגלו באוטומט זה צורות המראות התנהגויות מורכבות ומעניינות (כפי שיודגם בפיסקה הבאה), התגלה שהאוטומט שקול למכונת טיורינג, כלומר כל חישוב שניתן לבצע על מחשב כלשהו ניתן לביצוע בעזרת משחק החיים, ובנוסף הועלו השערות בקשר לשאלה האם אכן ניתן לייצר חיים, והאם ניתן לייצר יצורים חושבים בעזרת המשחק.
דחיפה נוספת לאוטומטים תאיים באה בזכות עבודותיו של סטיבן וולפרם. וולפרם פרסם בתחילת שנות ה-80 סדרה של מאמרים שבה הוא חקר אוטומטים תאיים חד-ממדיים, והראה שלמרות פשטותם הם מראים התנהגויות מורכבות. על מנת לחקור אוטומטים אלו הוא פיתח את תוכנת המחשב Mathematica שזכתה להצלחה מסחרית רבה. ההצלחה המסחרית של התוכנה ביססה אותו כלכלית וניתקה אותו מהצורך לנהל חיים אקדמיים רגילים. מסיבה זו לא פרסם באופן סדיר את תוצאות מחקריו הנמשכים אודות אוטומטים תאיים, אלא אגר אותן ולבסוף פרסם אותן כמקשה אחת בספרו: "A new kind of science".
דחיפה נוספת וחשובה לאוטומטים תאיים באה בדמות הצעה לפירוש דטרמיניסטי של תורת הקוונטים באמצעות אוטומטים תאיים של זוכה פרס נובל בפיזיקה Gerard 't Hooft שפרסם שורת מאמרים בנושא שהתפתחו לאינטרפטציה חדשה לתורת הקוונטים [1]
משחק החיים של קונויי
 ערך מורחב – משחק החיים (אוטומט תאי)
ערך מורחב – משחק החיים (אוטומט תאי)

אוטומט זה מתקיים על לוח משבצות דו ממדי, כאשר לכל משבצת שני מצבים: שחור (תא חי) או לבן (תא מת). משבצת שחורה תישאר שחורה בדור הבא אם יש לה שניים או שלושה שכנים שחורים (אחרת היא 'תמות' - ממחנק, כאשר יש לה יותר מדי שכנים, או מ'בדידות', כאשר יש לה מעט מדי שכנים), ומשבצת לבנה תהפוך לשחורה אם יש לה בדיוק 3 שכנים שחורים. לתא יש עד 8 שכנים (סביבת מור).
משחק החיים מכיל בתוכו סוגים שונים של יצורים והתנהגויות:
- מקרים שבהם כל התאים מתים לאחר זמן מה,
- מצבים נייחים – מצבים שבהם לא קורה דבר, למשל מצב של ריבוע בגודל 2X2 שכל ארבע משבצותיו שחורות.
- מצבים שמבצעים תנועה מחזורית. כך לדוגמה אם נתחיל במצב המורכב משורה של 3 משבצות שחורות, בתור הבא נקבל טור אנכי של 3 משבצות שחורות, ותור לאחר מכן נקבל חזרה 3 משבצות שחורות בשורה.
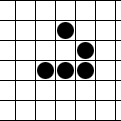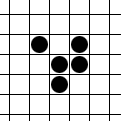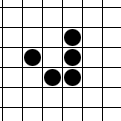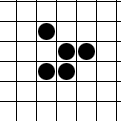
- אחד היצורים המעניינים ביותר במשחק הוא ה'גלשן' הנראה באיור. הגלשן מבצע תנועה מחזורית, אבל גם מתקדם תוך כדי תנועה.
משחק החיים הוצג לראשונה לקהל הרחב בטור של מרטין גרדנר בירחון "Scientific American". אחד האתגרים שהועלו במאמרים אלו היא השאלה האם ניתן לחשוב על מצב שבו התאים השחורים ילכו ויתרבו לעד? תשובה חיובית לשאלה הזאת נמצאה עם גילוי 'אקדח הגלשנים' הנראה באנימציה השנייה. בצורה זאת ישנה צורה המבצעת תנועה מחזורית אשר במהלכה היא משחררת גלשן ההולך ומתרחק ממנה.
אוטומטים חד-ממדיים


גם אוטומטים פשוטים מ"משחק החיים" מאפשרים התנהגות מורכבת ולא צפויה. דוגמה לכך הם אוטומטים חד-ממדיים. באוטומטים אלו מתחילים בשורה של משבצות, וכל משבצת מתפתחת בהתאם למצב שלה ושל שתי המשבצות הסמוכות אליה. את ההתפתחות של האוטומטים האלו בזמן ניתן לראות בעזרת תמונה דו-ממדית שבה כאשר יורדים שורה, זה שקול להתפתחות של צעד אחד בזמן.
דוגמה אחת לכלל כזה היא שמשבצת תהיה שחורה בדור הבא בתנאי שהיא או המשבצת שלימינה (אך לא שתיהן גם יחד) שחורות. היא תהיה לבנה אם היא והמשבצת שלימינה הן באותו צבע (לבן או שחור). אם מתחילים אוטומט זה במצב של שורה שבה רק המשבצת האמצעית שחורה, אזי האוטומט מייצר את הפרקטל הקרוי משולש שרפינסקי.
בספר "A new kind of science" סטיבן וולפרם מראה שאפילו אוטומטים חד-ממדיים פשוטים מאוד יכולים ליצור התנהגויות מסובכות. וולפרם מחלק את האוטומטים ומסווגם למספר קבוצות:
- ישנם אוטומטים אשר יוצרים התנהגות פשוטה: כאלו שעבורם כל המשבצות הופכות מיד לשחורות או לבנות, או אוטומטים שבהם התאים מבצעים התנהגות מחזורית פשוטה. דוגמה לאוטומטים כאלו הוא אוטומט שבו כל משבצת לא משנה מצבה תהפוך לבנה בתור הבא, או אוטומט שבו משבצת לבנה הופכת לשחורה, ומשבצת שחורה הופכת ללבנה.
- אוטומטים פרקטליים – אוטומטים אלו כמו בדוגמה של משולש שרפינסקי, יוצרים תבניות החוזרות על עצמן בגדלים שונים.
- אוטומטים אקראיים – אוטומטים אלו, אף אם מתחילים אותם מתבנית התחלתית פשוטה, יוצרים התנהגות מורכבת שנראית אקראית לחלוטין.
- אוטומטים סמי-אקראיים – באוטומטים אלו נוצרים שילוב של אזורים אקראיים ואזורים פרקטליים.
ראו גם
קישורים חיצוניים
- אוטומט תאי, באתר MathWorld (באנגלית)
- אוטומט תאי, באתר אנציקלופדיה בריטניקה (באנגלית)
- אוטומט תאי באתר LifeWiki
- סיווג וולפרם של אוטומטים תאיים כולל דוגמאות באתר LifeWiki
הערות שוליים
- ↑ Matthew Cook, Universality in Elementary Cellular Automata, Complex Systems 15, 2004, pp. 1–40
אוטומט תאי35185939Q189156


