אבולוט

אבולוט של אליפסה הוא אסטרואידה מתוחה בציר המשני של האליפסה

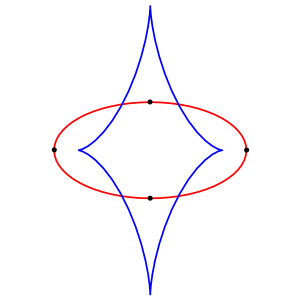
בגאומטריה דיפרנציאלית, בהינתן עקומה במישור $\gamma :[0,L]\to {\mathbb{ℝ}}^2$ בפרמטריזציה טבעית, אֵבוֹלוּט (באנגלית: Evolute; בעברית: לָפוּף) מוגדר כמקום הגאומטרי של כל מרכזי העקמומיות שלה.

נוסחת האבולוט היא:

$\overrightarrow{E}(s)=\overrightarrow{\gamma }(s)+R(s)\overrightarrow{n}(s)=\overrightarrow{\gamma }(s)+\frac{1}{k(s)}\overrightarrow{n}(s)$

כאשר

• k היא העקמומיות של העקומה $\gamma$ (המתקבלת לפי משוואות פרנה מתוך $\frac{d\overrightarrow{v}}{ds}={\overrightarrow{v}}^{\prime }(s)=k(s)\overrightarrow{n}(s)$, או בנוסחה מפורשת $k(s)=⟨{\overrightarrow{\gamma }}^{″}(s),\overrightarrow{n}(s)⟩$)
• $R(s)=\frac{1}{k(s)}$ הוא רדיוס העקמומיות
• $\overrightarrow{n}(s)$ הוא וקטור יחידה הניצב לווקטור המשיק לעקומה $\overrightarrow{v}(s)={\overrightarrow{\gamma }}^{\prime }(s)$ ויוצר עמו בסיס אורתונורמלי בעל אוריינטציה חיובית.

אנליטית, ניתן לתאר את האבולוט כתמונה הסינגולרית של ההעתקה

$(\tau ,s)⟼\overrightarrow{F}(\tau ,s)=\overrightarrow{\gamma }(s)+\tau \overrightarrow{n}(s)$.

במקום זה, המתקבל עבור $\tau =1/k(s)$, הנורמלים בנקודות קרובות איניפיניטסימלית נחתכים ולכן $(\tau ,s)$ לא מהווים מערכת קואורדינטות מוגדרת היטב. מכאן נובע שהאבולוט הוא מעטפת של כל הנורמלים לעקומה.^{[דרושה הבהרה]}

משפט שימושי לחישוב אורך של קשת (רגולרית ובלי קודקודים, כלומר: $k(s),k^{\prime }(s)\ne 0$) על האבולוט טוען שאורך הקשת שווה להפרש רדיוסי העקמומיות בנקודות הקצה:

$\underset{s_1}{\overset{s_2}{\int }}|E^{\prime }(s)|ds=\underset{s_1}{\overset{s_2}{\int }}|(\frac{d}{ds}{R}^{\prime }(s))\overrightarrow{n}(s)|ds=\underset{s_1}{\overset{s_2}{\int }}|R^{\prime }(s)|ds=|\underset{s_1}{\overset{s_2}{\int }}{R}^{\prime }(s)ds|=|R(s_2)-R(s_1)|$

כאשר המעבר הלפני האחרון נעשה מאחר ש-R היא פונקציה מונוטונית (עולה או יורדת) של s בקשת רגולרית, ו-

${\overrightarrow{E}}^{\prime }(s)={\gamma }^{\prime }(s)+R^{\prime }(s)\overrightarrow{n}(s)+R(s){\overrightarrow{n}}^{\prime }(s)=\overrightarrow{v}(s)+R^{\prime }(s)\overrightarrow{n}(s)-R(s)k(s)\overrightarrow{v}(s)=R^{\prime }(s)\overrightarrow{n}(s)$

לפי משוואות פרנה.

הדיון הראשון באבולוט נמצא בכרך ה-V של הספר "חרוטים" ("Conics") מאת אפולוניוס (בסביבות 200 לפני הספירה), אך מי שנחשב לראשון שלמד אותם בצורה יסודית הוא כריסטיאן הויגנס (1673).

קישורים חיצוניים

• אבולוט, באתר MathWorld (באנגלית)
• אבולוט, ב-MathWorld של אריק ויינשטיין
• Yates, R. C.: A Handbook on Curves and Their Properties, J. W. Edwards (1952), "Evolutes." pp. 86ff
• Evolute on 2d curves.

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

אבולוט37964849Q658654