המבנה הדק

תמונת התאבכות המראה את פיצול המבנה הדק עבור אטום דאוטריום.

בפיזיקה אטומית, תיקוני המבנה הדק מתארים את פיצול הקווים הספקטרליים של אטומים, בעיקר עקב אפקטים יחסותיים מסדר ראשון ואינטראקציית ספין-מסלול.

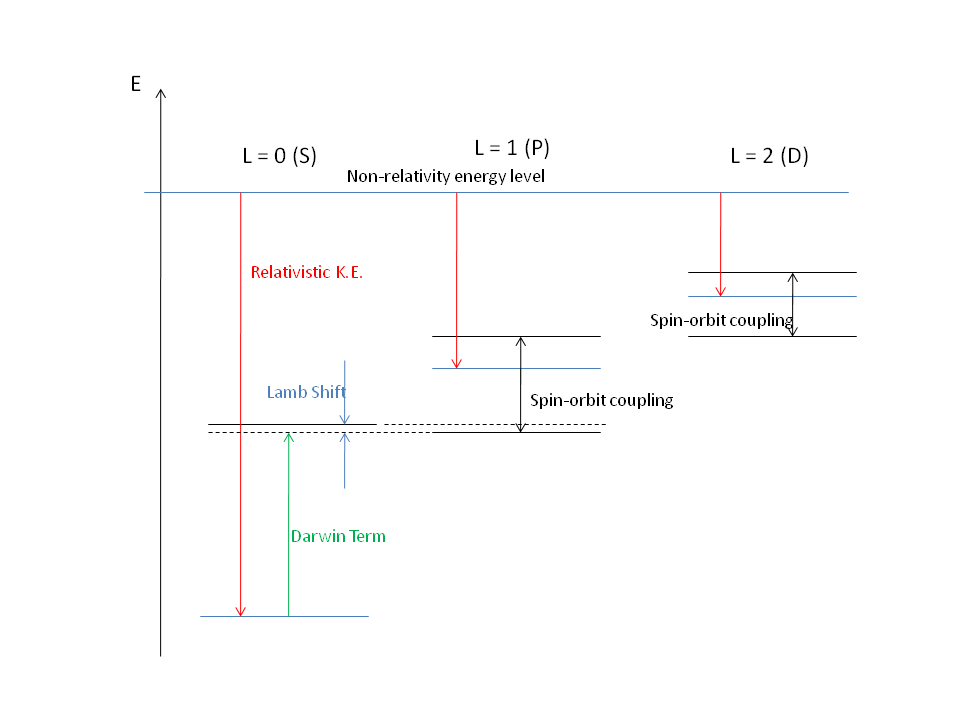
הספקטרום הראשי של אטום המימן הוא הספקטרום הצפוי ללא תיקונים יחסותיים וללא התייחסות לספין והשפעותיו. עבור אטום המימן רמות האנרגיה בספקטרום הראשי מושפעות רק מהמספר הקוונטי הראשי, n, ואילו מודל מדויק יותר יקח בחשבון גם אפקטים יחסותיים ואפקטים הקשורים בספין האלקטרון. כאשר מתחשבים באפקטים אלו נעלם ניוון רמות האנרגיה הנחזה ממשוואת שרדינגר והקווים הספקטרליים מתפצלים. גודל תיקון המבנה הדק קטן פי ²(Zα), כאשר Z הוא המספר האטומי ו-α הוא קבוע המבנה הדק, מספר חסר יחידות השווה בקירוב ל־$\frac{1}{137}$.

המבנה הדק מורכב משלושה איברי תיקון: איבר האנרגיה הקינטית (מכונה גם "איבר מסה"), איבר צימוד ספין-מסלול, ו"איבר דרווין". ההמילטוניאן המלא נתון על ידי:

$H=H_0+H_{\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}+H_{\mathrm{s}\mathrm{o}}+H_{\mathrm{D}\mathrm{a}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}}$.

כאשר $H_0$ הוא ההמילטוניאן המקורי (כלומר ללא התחשבות בספין ותיקונים יחסותיים).

רקע

ערך מורחב – אטום המימן

על פי המודל הקוונטי הבסיסי של אטום המימן, ישנם אורביטלים (פונקציות גל אלקטרוניות, או בשפה ציורית יותר מסלולי האלקטרונים) הממוספרים לפי שלושה מספרים קוונטיים: $n,\ell ,m$: המספר $n$ הוא המספר הקוונטי הראשי, ונקרא גם רמת האנרגיה, והוא היחיד (במודל הפשוט) אשר משפיע על אנרגיית הארביטלים. המספרים $\ell ,m$ מייצגים תנע זוויתי ואינם משפיעים על האנרגיה של האורביטל. מצב כזה, שבו מספר אלקטרונים חולקים את אותה רמת אנרגיה נקרא ניוון קוונטי. בפועל מתברר שרמות האנרגיה באטום אינן מנוונות, לפי ניסויי ספקטרוסקופיית בליעה אטומית שבהם מודדים את הפרש האנרגיה בין הרמות. במילים אחרות ישנו הבדל אנרגטי בין מצבים שונים בעלי אותו מספר קוונטי ראשי. מודלים מורכבים יותר, אשר לוקחים בחשבון תיקונים יחסותיים ואחרים למודל הפשוט, מנבאים בצורה מדויקת מאד את רמות האנרגיה של אטום המימן, והמודל המדויק ביותר (מדויק לחלוטין עד כדי דיוק הניסויים כיום) הוא אלקטרודינמיקה קוונטית.

איבר האנרגיה הקינטית (איבר מסה)

בדרך כלל, איבר האנרגיה קינטית של ההמילטוניאן נתון על ידי

$T=\frac{p^2}{2m}$

כאשר m היא מסת החלקיק ו־p הוא התנע הקווי שלו. עם זאת, כאשר מתחשבים בתורת היחסות הפרטית, האנרגיה הקינטית נתונה בביטוי,

$,T=\sqrt{p^2{c}^2+m^2{c}^4}-m{c}^2$

שבו האיבר הראשון הוא סך האנרגיה היחסותית, והאיבר השני הוא אנרגיית המנוחה של האלקטרון (c היא מהירות האור), בסימן שלילי. בהנחה שמתקיים $pc\ll m{c}^2$, ניתן לקרב את הביטוי בעזרת האיברים הראשונים של טור טיילור ב־$(p/mc{)}^2$, ולקבל שהתיקון מסדר ראשון להמילטוניאן הוא:

$H_{\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}=-\frac{p^4}{8m^3{c}^2}$

המצבים העצמיים של ההמילטוניאן הלא מופרע נתונים בביטוי:

$,E_n=-\frac{e^2}{2a_0{n}^2}$

שבו $a_0$ הוא רדיוס בוהר ו־$n$ הוא המספר הקוונטי הראשי. בעזרת תורת ההפרעות, ניתן לחשב מהתיקון להמילטוניאן את התיקון הנובע ממנו לאנרגיה:

$E_n^{(1)}=-\frac{E_n^2}{2m{c}^2}(\frac{4n}{\ell +1/2}-3)$

כאשר $\ell$ הוא המספר הקוונטי של התנע הזוויתי.

מכאן, שסדר הגודל של התיקון היחסותי לאנרגיה הוא $-10^{-5}\text{eV}$.

הוכחה

כאמור, $T=\sqrt{p^2{c}^2+m^2{c}^4}-m{c}^2=m{c}^2(\sqrt{1+\frac{p^2}{m^2{c}^2}}-1)$ אם מפתחים את השורש כטור טיילור ב-$(p/mc{)}^2$, מקבלים $T=m{c}^2[1+\frac{1}{2}{\left(\frac{p}{mc}\right)}^2-\frac{1}{8}{\left(\frac{p}{mc}\right)}^4+O{\left(\frac{p}{mc}\right)}^6]-m{c}^2$ $=\frac{p^2}{2m}-\frac{p^4}{8m^3{c}^2}+\cdots$ כלומר, התיקון מסדר ראשון להמילטוניאן הוא: $H_{\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}}=-\frac{p^4}{8m^3{c}^2}$ ומכאן, בעזרת תורת ההפרעות, שהתיקון הראשון לאנרגיה הוא: $E_n^{(1)}=⟨{\psi }_n^{(0)}|H^{\prime }|{\psi }_n^{(0)}⟩=-\frac{1}{8m^3{c}^2}⟨{\psi }_n^{(0)}|p^4|{\psi }_n^{(0)}⟩=-\frac{1}{8m^3{c}^2}⟨{\psi }_n^{(0)}|p^2{p}^2|{\psi }_n^{(0)}⟩$ כאשר $|{\psi }_n^{(0)}⟩$ הוא מצב עצמי של ההמילטוניאן הלא מופרע, כלומר: $H^0|{\psi }_n^{(0)}⟩=E_n|{\psi }_n^{(0)}⟩$ $(\frac{p^2}{2m}+V)|{\psi }_n^{(0)}⟩=E_n|{\psi }_n^{(0)}⟩$ $p^2|{\psi }_n^{(0)}⟩=2m(E_n-V)|{\psi }_n^{(0)}⟩$ ובתוצאה זו ניתן להיעזר כדי לחשב: $E_n^{(1)}=-\frac{1}{8m^3{c}^2}⟨{\psi }_n^{(0)}|p^2{p}^2|{\psi }_n^{(0)}⟩$ $E_n^{(1)}=-\frac{1}{8m^3{c}^2}⟨{\psi }_n^{(0)}|(2m{)}^2(E_n-V{)}^2|{\psi }_n^{(0)}⟩$ $E_n^{(1)}=-\frac{1}{2m{c}^2}(E_n^2-2E_n⟨V⟩+⟨V^2⟩)$ עבור אטום המימן, $V=\frac{e^2}{r};⟨V⟩=\frac{-e^2}{a_0{n}^2};⟨V^2⟩=\frac{e^4}{(\ell +1/2)n^3{a}_0^2}$ לכן, התיקון היחסותי לאטום המימן נתון בנוסחה: $E_n^{(1)}=-\frac{1}{2m{c}^2}(E_n^2+2E_n\frac{e^2}{a_0{n}^2}+\frac{e^4}{(\ell +1/2)n^3{a}_0^2})=-\frac{E_n^2}{2m{c}^2}(\frac{4n}{\ell +1/2}-3)$ בעזרת הערכים העצמיים של ההמילטוניאן הלא מופרע: $E_n=-\frac{e^2}{2a_0{n}^2}$ הערה: במציאות, $p^4$ הוא לא אופרטור הרמיטי עבור אלקטרונים באטום דמוי־מימן באורביטל-s (כלומר, $\ell =0$). לשם שימוש בתורת ההפרעות נדרש שההמילטוניאן המופרע יהיה הרמיטי. בשל כך, ההוכחה למעלה לא ריגורוזית לחלוטין כאשר $\ell =0$. עם זאת, השוואה עם התוצאה המדויקת (תוך שימוש במשוואת דיראק) מראה שהתוצאה למעלה נכונה עבור התיקון מסדר ראשון אפילו במצב בו $\ell =0$.

איבר צימוד ספין-מסלול

$H_{so}=\frac{1}{2}\left(\frac{Z{e}^2}{4\pi {ϵ}_0}\right)\left(\frac{g_s}{2m_e^2{c}^2}\right)\frac{\overrightarrow{L}\cdot \overrightarrow{S}}{r^3}$

איבר התיקון השני, איבר הצימוד ספין-ממסלול, נובע מעבודה במערכת הייחוס של האלקטרון בה האלקטרון נייח ואילו הגרעין מקיף אותו לעומת מערכת היחוס הסטנדרטית בה האלקטרון מקיף את הגרעין. במצב זה ניתן להתייחס לגרעין המקיף את האלקטרון כלולאת זרם היוצרת שדה מגנטי $\overrightarrow{B}$. בנוסף לכך לאלקטרון עצמו יש תנע זוויתי אינטרינזי (ספין). בין השדה המגנטי $\overrightarrow{B}$ לבין המומנט המגנטי ${\overrightarrow{\mu }}_s$ יש צימוד ומכאן מתקבל התיקון הבא:

$\mathrm{\Delta }{E}_{SO}=\xi (r)\overrightarrow{L}\cdot \overrightarrow{S}$

בפועל, התיקון הזה אינו מדויק, ויש להכפיל אותו במקדם $\frac{1}{2}$. מקדם זה נובע העובדה שעברנו למערכת היחוס הלא אינרציאלית של האלקטרון. הוא התגלה על ידי לואלין תומאס ונקרא "מקדם תומאס" (או: "פקטור תומאס") על שמו.

מכיוון שמתקיים

$⟨\frac{1}{r^3}⟩=\frac{1}{n^3{a}_0^3}\frac{1}{\ell (\ell +\frac{1}{2})(\ell +1)}$

$⟨\overrightarrow{L}\cdot \overrightarrow{S}⟩=\frac{{\hslash }^2}{2}(j(j+1)-\ell (\ell +1)-s(s+1))$

ערך התצפית של ההמילטוניאן יהיה:

$⟨H_{SO}⟩=\frac{E_n{}^2}{m_e{c}^2}\left(n\frac{j(j+1)-\ell (\ell +1)-\frac{3}{4}}{\ell (l+\frac{1}{2})(\ell +1)}\right)$

ולכן סדר הגודל של איבר התיקון צימוד ספין-מסלול הוא $\frac{Z}{n^3}10^{-5}\text{ eV}$. מכאן שככל שהאטום כבד יותר (מספרו האטומי Z גבוה יותר), איבר צימוד ספין-מסלול משמעותי יותר.

הערה: רמות האנרגיה תלויות ביחס הג'ירומגנטי, שהוא גודל הקושר בין המומנט המגנטי $\mu$ לספין $s$ והוא אחת מתכונות החלקיק. עבור אלקטרון הוא בקירוב $2$, עבור פרוטון כ-$2.79$ ועבור נייטרון ערכו $-1.91$. רמות האנרגיה $(n,\ell ,s)=(n,0,1/2)$ ו־$(n,\ell ,s)=(n,1,-1/2)$ זהות לאחר תיקון המבנה הדק, כאשר משתמשים בפקטור ג'ירומגנטי 2. עבור תיקונים בסדרים גבוהים יותר יש להשתמש בפקטור ג'ירומגנטי של 2.0031904622.

מהכללה לכל סדר של התיקונים היחסותיים (משוואת דיראק) מוצאים שלזוג רמות האנרגיה האלו יש ניוון (רמות האנרגיה זהות), אך מאוחר יותר נתגלה שאין ניוון כתוצאה מתורת השדות הקוונטית.

איבר דרווין

$E_{\mathrm{D}\mathrm{a}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{n}}=\frac{{\hslash }^2}{8m_e^2{c}^2}4\pi \left(\frac{Z{e}^2}{4\pi {ϵ}_0}\right){\delta }^3\left(\overrightarrow{r}\right)$

$E_{\mathrm{D}\mathrm{a}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{n}}=\frac{{\hslash }^2}{8m_e^2{c}^2}4\pi \left(\frac{Z{e}^2}{4\pi {ϵ}_0}\right)|\psi (0{)}^2|$

$\psi (0)=0\text{ for }\ell >0$

$\psi (0)=\frac{1}{\sqrt{4\pi }}2{\left(\frac{Z}{n{a}_0}\right)}^{\frac{3}{2}}\text{ for }\ell =0$

$E_{\mathrm{D}\mathrm{a}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{n}}=\frac{2n}{m_e{c}^2}{E}_n^2$

לכן איבר דרווין משפיע רק על מצבי s. לדוגמה, האיבר נותן למצב 2s את אותה אנרגיה כמו למצב 2p על ידי העלאת מצב 2s ב־$9.057\cdot {\text{10}}^{-5}eV$.

איבר דרווין, על שם צ'ארלס גלטון דרווין, משנה את הפוטנציאל האפקטיבי בגרעין. ניתן לפרש את השפעתו כמריחת האינטרקציה בין האלקטרון לגרעין בשל אפקט הרעידה הקוונטית של האלקטרון.

תיקון לם, על שם ויליס לם, הוא תיקון המשפיע רק על מצבי-s ואין לבלבל בינו לבין איבר דרווין. איבר דרווין משווה את האנרגיה של מצבי-s ומצבי-p ואילו תיקון לם מעלה את האנרגיה של מצבי-s מעל האנרגיה של מצבי-p.

האפקט הכולל

האפקט הכולל הוא סכום של שלושת האפקטים והוא ניתן על ידי הביטוי הבא:

$,\mathrm{\Delta }E=-\frac{m_e{c}^2(Z\alpha {)}^4}{2n^3}(\frac{1}{j+1/2}-\frac{3}{4n})$

כאשר $j$ הוא המומנט הזוויתי הכולל: ($j=1/2$ אם $\ell =0$ ו־$j=\ell \pm 1/2$ אחרת).

לתוצאה זו הגיע ראשון ארנולד זומרפלד על בסיס התאורייה של בוהר (התאוריה הקוונטית הישנה), לפני שפותחה תאוריית הקוונטים המודרנית.

ראו גם

• מכניקת הקוונטים
• קבוע המבנה הדק
• המבנה העל-דק

לקריאה נוספת

• Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
• Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.

קישורים חיצוניים

• המבנה הדק, אתר hyperphysics (באנגלית)
• המבנה הדק של אטום המימן, אתר אוניברסיטת טקסס (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

שגיאות פרמטריות בתבנית:מיון ויקיפדיה
שימוש בפרמטרים מיושנים [ דרגה ] המבנה הדק23330591