כללי דה מורגן
כללי דה מורגן, הקרויים על-שמו של המתמטיקאי והלוגיקן בן המאה ה-19, אוגוסטוס דה מורגן, הם שני כללים בלוגיקה, בתורת הקבוצות ובאלגברה בוליאנית (בפרט, לוגיקה בוליאנית), הקושרים את הפעולות הבסיסיות בתחומים אלה.
- לוגיקה: הכללים קושרים את הפעולות "או", "גם", "לא". באופן מילולי בכתיב לא פורמלי, קובעים הכללים כי השלילה של- קיום א' וגם קיום ב', היא אי קיום א' או אי קיום ב'; וכן כי השלילה של קיום א' או קיום ב', היא אי קיום א' וגם אי קיום ב'.
בכתיב פורמלי הם מוצגים כך:
- $ \neg (P\wedge Q)\equiv (\neg P)\vee (\neg Q) $
- $ \neg (P\vee Q)\equiv (\neg P)\wedge (\neg Q) $
לדוגמה, המשפט "היום לא יום ראשון או שלא יורד עכשיו גשם" שקול לוגית למשפט: "לא נכון ש'היום יום ראשון וגם יורד עכשיו גשם'"
|
| |
|
||
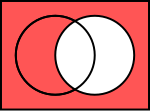
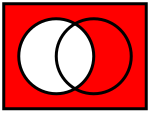
| הדגמה של אחד הכללים בעזרת דיאגרמת ון. שתי התמונות העליונות הן המשלימים של הקבוצות המיוצגות על ידי המעגלים. התמונה התחתונה מייצגת את החיתוך שלהן- השטח המשותף שלהן | ||
- $ (A\cap B)^{C}=A^{C}\cup B^{C} $
- $ (A\cup B)^{C}=A^{C}\cap B^{C} $
ובאופן כללי: $ \ \left(\bigcup _{}A_{i}\right)^{C}=\bigcap _{}A_{i}^{C} $, ו-$ \ \left(\bigcap _{}A_{i}\right)^{C}=\bigcup _{}A_{i}^{C} $
- אלגברה בוליאנית: הכללים קושרים את הפעולות "חיבור", "כפל", "שלילה".
- בהתאם להגדרת השלילה, הביטוי '(P+Q) הוא שלילת הביטוי (P+Q), ועל כן יקבל ערך אמת רק אם P+Q הוא בעל ערך 0, כלומר ערך שקרי. כללי דה מורגן קובעים כי שלילת P+Q זהה למכפלת שלילת P בשלילת Q, ואילו שלילת P*Q זהה לחיבור שלילת P עם שלילת Q. בכתיב פורמלי הם מוצגים כך:
- $ (P+Q)^{\prime }=P'\cdot Q' $
- $ \!\,(P\cdot Q)'=P'+Q' $
או כך:
- $ {\overline {p+q}}={\bar {p}}\cdot {\bar {q}} $
- $ {\overline {p\cdot q}}={\bar {p}}+{\bar {q}} $
למעשה, ההבדל בין הגרסאות השונות לניסוח הכלל אשר הוצגו לעיל הוא בסימון בלבד.
שימוש בכללי דה מורגן
לכללים אלה מספר שימושים, ביניהם:
- פישוט של ביטויים מתחומי הלוגיקה והמתמטיקה המתוארים לעיל.
- פישוט התניות בעת כתיבת תוכניות מחשב.
- שימוש באלקטרוניקה ספרתית (בה במקרים רבים נעשה שימוש בשתי רמות מתח בלבד) לצורכי פישוט תכנונם של מעגלים חשמליים, למשל, כאלה העושים שימוש בשערים לוגיים.
- ניתן לעשות שימוש בכללים אלה לצורך ייצוג של ביטויים על ידי שימוש בסוג אחד בלבד של פעולות, למשל פעולות NAND. להרחבה ראו הערך NAND לוגי.
הוכחה
ההוכחה של כללי דה-מורגן מתבצעת באינדוקציה שלמה. כלומר, הצבה של כל הצירופים האפשריים בכל אחד מהפסוקים, נותנת ערכים שווים. כך, אם נציב ערכי אמת ב-P וב-Q, אזי הביטוי (P+Q) יקבל את הערך "אמת" והביטוי '(P+Q), ערכו יהי שקר, כמו גם ערכו של 'p'*q. לאחר הצבת כל הצירופים האפשריים של P ו-Q מתקבל, למעשה, הכלל.
הכלל בנוגע לתורת הקבוצות, ניתן להוכחה על נקלה בעזרת הכללים הנ"ל, זאת, בהינתן ההגדרות של חיתוך, איחוד ומשלים של קבוצה. ההוכחה היא כדלהלן:
$ a\in (A\cap B)^{C} $
$ \iff a\not \in (A\cap B) $
$ \iff \neg (a\in (A\cap B)) $
$ \iff \neg (a\in A\wedge a\in B) $
$ \iff (a\not \in A)\vee (a\not \in B) $
$ \iff a\in A^{C}\vee a\in B^{C} $
$ \iff a\in A^{C}\cup B^{C} $ובצורה דומה מוכח גם המשפט השני.
קישורים חיצוניים
- כללי דה מורגן, באתר MathWorld (באנגלית)
כללי דה מורגן36733648Q173300