פלקסגון
פלקסגון הוא מודל מצולע שטוח שנוצר מקיפול רצועות ישרות או עקומות העשויות לרב מנייר. מודלים אלו בעלי היכולת לשנות את פניהם כאשר הם מקופלים (flexed).
יש פלקסגונים המורכבים ממצולעים שונים: משולשים, מרובעים, טרפזים, מחומשים, משושים ועוד.
מקור השם הוא המילה Flexagon שהיא צרוף של המילים גמיש=Flexible ומצולע=Polygon.
אפשר להכין הקספלקסגון על ידי קיפול רצועה באופן שתיצור משושה בעל מספר רב של צדדים. כמות הצדדים תלויה במספר המשולשים ששימשו ליצירתו.
ההקספלקסגון (hexaflexagon) מורכב ממשושה ומכונה גם "משושה אוריגמי" (Origami hexagon)[1]. כינוי הפלקסגון תלוי מהמצולע שממנו מורכב ובמספר הפנים שיש לו.
למשל הטריהקספלסגון (trihexaflexagon) הוא פלקסגון בצורת משושה (hexa) בעל 3 פנים (tri).
על פי רוב מכינים פלקסגונים מנייר, אך ניתן גם להשתמש בחומרים אחרים הניתנים לקיפול כמו בד, סריג או בצק.
היסטוריה, התפתחות ומחקר
הפלקסגון התגלה על ידי ארתור סטון (Arthur H. Stone) בשנת 1939, אשר היה סטודנט בריטי באוניברסיטת פרינסטון שבארצות הברית[2][1][3]. עם השנים הגיע סטון למשרת פרופסור למתמטיקה באוניברסיטת רוצ'סטר[2].
בתחילת דרכו כסטודנט סטון הביא איתו דפי כתיבה בגודל A4 המקובל באירופה, אך גילה שהדפים חורגים מגבולות הקלסר המיועד לנייר בגודל אמריקאי. כדי להתאים את דפי הכתיבה לגודל הקלסר הוא גזר את הנייר העודף ונשאר עם כמות גדולה של רצועות נייר. הוא נמנע מלזרוק את הרצועות לפח האשפה ובמקום זאת החל לקפל אותן למשולשים שווי צלעות בדרכים שונות, אשר אחת מהן יצרה את צורת המשושה טריהקספלקסגון[3].
סטון הראה את הפלקסגון לריצ'רד פיינמן, בריאנט טאקר (Bryant Tucker) וג'ון טאקי (John Tukey), אשר השקיעו זמן רב לקיטלוג של פלקסגונים[3]. ריצ'רד פיינמן בנה דיאגרמה אשר מתארת את אפשרויות המעבר בין ששת הצדדים השונים של ההקסופלקסגון. מדיאגרמה זו הוא קיבלת את ההשראה שהובילה אותו לפיתוח דיאגרמת פיינמן[2], אשר מייצגת תהליכים בתורת השדות הקוונטית באמצעות מסלולי חלקיקים. מקרה זה הוא דוגמה לדרך בה שעשועי מתמטיקה יכולים להוביל להתפתחויות בתחום המדע.
סוגי פלקסגונים
המושג "פלקסגון" משמש גם ככינוי כללי לדברים גמישים וקלים לקיפול, אשר יכולים ליצור צורות שונות[1]. בהתאם לכך, ישנם גם פלקסגונים בצורות שאינן משושה. לדוגמה ה-tetraflexagon הוא בצורת מרובע[1].
יצירה של הקספלקסגון
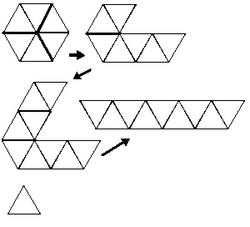
ניתן לייצר הקספלקסגון מרצועה המקופלת למשולשים שווי שוקיים. מקור השם הקספלקסגון הוא מהשילוב של המילה פלקסגון עם המילה hexa שפרושה 6[1].
לצורך יצירת פלקסגון בסיסי בעל שלושה צדדים נעשה שימוש ברצועה המקופלת ל-9 משולשים. בנוסף ניתן להשתמש ברצועה ארוכה יותר בעלת 18 משולשים ליצירת פלקסגון המורכב מ-6 צדדים.
בכל מקרה ניתן להוסיף משולש נוסף לצורך הדבקה נוחה יותר של קצוות רצועת הנייר. במצב זה המשולש הראשון של הצד העליון של הרצועה יודבק למשולש האחרון של הצד התחתון של הרצועה. אין חשיבות לאופן שבו הם מודבקים, כלומר - הראשון יכול להיות מודבק על האחרון או להפך[2].
צדדיו של ההקספלקסגון
באופן כללי כל אחד מצדדיו ההקספלקסגון בנוי מ-6 משולשים שווי צלעות, הצמודים אחד לשני בקודקודם באופן היוצר משושה[2]. על ידי הצמדתם של כל שני משולשים סמוכים, ניתן לחשוף צד חדש מהמרכז של הפלקסגון[1]. כיוונם של המשולשים יכול להשתנות ממצב למצב, כך שלעיתים הם יפנו כלפי חוץ ולעיתים כלפי פנים. עם זאת, אותם המשולשים תמיד יופיעו יחדיו באותו הצד[2].
כאמור, לפלקסגון הפשוט הבנוי מ-9 משולשים יש שלושה צדדים. במקרה זה בכל מצב נתון צד אחד יפנה כלפי מעלה, השני כלפי מטה והצד השלישי יהיה מוסתר[2].
צידה היחיד של רצועת הפלקסגון
כאמור, הפלקסגון מורכב מרצועה מקופלת. במקור לרצועה יש שני צדדים - עליון ותחתון. אולם, צורת הקיפול שלה משנה מצב זה. זאת משום שכאשר מצמידים רצועה שמסובבת בכפולות אי-זוגיות של 180 מעלות, נוצר משטח ללא חלק פנימי או חיצוני[1].
צורת הקיפול של הרצועה המשמשת ליצירת הפלקסגון כוללת שלושה "חצאי סיבוב", באופן הדומה לטבעת מביוס[2]. ההבדל הוא שטבעת מביוס מקופלת ב-180 מעלות בעוד שהפלקסגון מקופל ב-540 מעלות (שהם שלוש פעמים 180 - כפולה אי זוגית)[1]. כתוצאה מכך, בעוד שלפלקסגון יש מספר רב של צדדים, לרצועה שממנו הוא מורכב יש רק צד אחד[2].
שימושים לחינוך והוראה
בתחום החינוך הפלקסגון יכול לשמש ככלי להוראה של נושאים שונים. במיוחד לאור זאת שצורת הקיפול שלו קלה ללימוד[3]. ניתן גם להדפיס לתלמידים מראש תבניות מוכנות שעליהן מסומנים המשולשים.
במסגרת למידת חקר הפלקסגון יכול לזמן לכל אחד מהתלמידים הזדמנות לבחון את הדפוסים השונים בקצב האישי שלו[3]. ניתן לעקוב אחרי כל הצירופים האפשריים של המשולשים על צדדיו המרובים של הפלקסגון על ידי ציור פרצופים בצבעים שונים בכל צד. כאשר הצדדים מופיעים בכיוונים שונים הפרצופים יהפכו ממחייכים לעצובים[2].
כמו צורות גאומטריות רבות, ניתן להעריך את הפלקסגון ברמות תחכום מתמטיות מרובות[3]. במסגרת הוראת המתמטיקה הוא יכול לשמש ללימוד מגוון מושגים מתחום הגאומטריה והאלגברה, כמו סימטריה וטרנספורמציה[3].
במסגרת לימודי האמנות ניתן להשתמש בפלקסגון ליצירה של ציורים בעלי אופי דינמי, משום שהם משתנים כאשר הופכים את צדדיו של הפלקסגון. משום שהרצועה המשמשת ליצירת הפלקסגון היא דו צדדית, כל קיפול מייצר שני משולשים הניתנים לציור. כלומר, בפלקסגון המורכב מ-9 משולשים ניתן לצייר על 9 שבצד האחד ועוד 9 בצד האחר - סה"כ 18. בדומה לזאת, לפלקסגון הבנוי מ-18 משולשים ניתן לצייר על 36 משולשים משני הצדדים של הרצועה[2]. דבר זה מאפשר גיוון רב.
ראו גם
קישורים חיצוניים
| מיזמי קרן ויקימדיה |
|---|
 ערך מילוני בוויקימילון: משושה אוריגמי |
| ערך מילוני בוויקימילון: פלקסגון |
 תמונות ומדיה בוויקישיתוף: פלקסגון |
- גמישושון משולש – פלקסגון! - הסבר על פלקסגון וסרטון הדרכה מהאתר כיתה בפיתה.
- איך מכינים פלקסגון - סרטון הדרכה
- Hexaflexagons - סדרת סרטונים של Vi Hart אודות ההיסטוריה של הפלקסגון, המעבר בין הצדדים השונים וטיפים לבנייה
הערות שוליים
- ^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Nishiyama, Y. (2010). General Solution for Multiple Foldings of Hexaflexagons.International Journal of Pure and Applied Mathematics, 58(1), 113-124.
- ^ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 Hilton, P., Pedersen, J., & Walser, H. (1997). The faces of the tri-hexaflexagon. Mathematics Magazine, 70(4), 243-251.
- ^ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Berkove, E. J., & Dumont, J. P. (2004). It's okay to be square if you're a flexagon. Mathematics Magazine, 77(5), 335-348.